Liên hệ giữa dây và khoảng cách từ tâm đến dây - Toán lớp 9

---

Liên hệ giữa dây và khoảng cách từ tâm đến dây

Với Liên hệ giữa dây và khoảng cách từ tâm đến dây Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Liên hệ giữa dây và khoảng cách từ tâm đến dây từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Định lý: Trong một đường tròn:

- Hai dây cung bằng nhau thì cách đều tâm,

- Hai dây cung cách đều tâm thì bằng nhau.

- Dây cung nào lớn hơn thì gần tâm hơn.

- Dây cung gần tâm hơn thì lớn hơn.

B. Bài tập tự luận

Bài 1: Cho hình vẽ sau, trong đó MN=PQ. Chứng minh rằng:

a, AE=AF

b, AN=AQ.

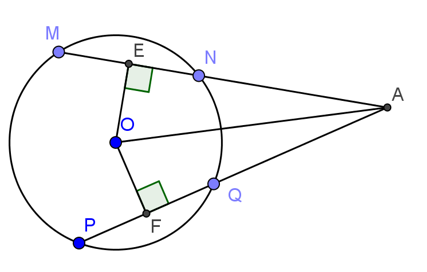
Hướng dẫn giải

Vì MN=PQ nên OE=OF( theo định lý liên hệ giữa dây và khoảng cách từ tâm đến dây)

Xét tam giác vuông AOE và tam giác vuông AOF có:

OE=OF ( chứng minh trên)

AO: chung

Suy ra ΔAOE = ΔAOF ( cạnh huyền-cạnh góc vuông)

Suy ra AE=AF( 2 cạnh tương ứng)(1)

Vì OE⊥MN nên ME=NE (tính chất đường kính và dây cung)

Vì OF⊥PQ nên PF=QF (tính chất đường kính và dây cung)

Mà MN=PQ

Suy ra ME=NE=PF=QF.(2)

Từ (1) và (2) suy ra AN=AQ.

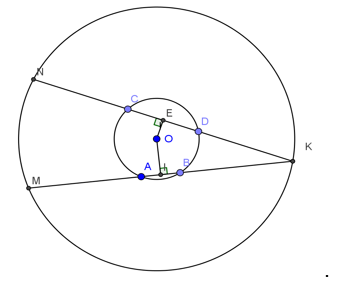
Bài 2: Cho đường tròn(O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O;OK) cắt KA và KC tại M và N.

Chứng minh KM < KN.

Hướng dẫn giải

Kẻ OI ⊥AB, OE ⊥ CD.

Xét đường tròn (O;OA) có: AB và CD là dây cung, AB < CD. Suy ra OI > OE.

Xét đường tròn (O;OK) có KN và KM là dây cung và OI > OE. Suy ra KM < KN.

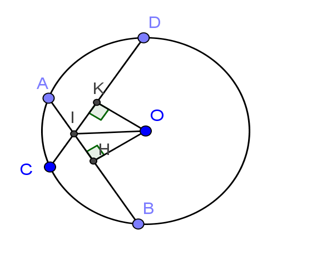
Bài 3: Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:

a, IO là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD.

b, Điểm I chia AB, CD thành các đoạn thẳng bằng nhau đôi một.

Hướng dẫn giải

a, Kẻ OH ⊥ AB; OK ⊥ CD.

Vì CD=AB nên OK=OH.

Xét tam giác vuông IKO và tam giac vuông IOH ta có:

OK=OH

IO: chung

Suy ra Δ IKO = ΔIOH ( cạnh huyền-cạnh góc vuông)

=> ∠KIO = ∠OIH ( 2 góc tương ứng)

Suy ra OI là tia phân giác của góc BID

b, Theo câu a, Δ IKO = ΔIOH ( cạnh huyền-cạnh góc vuông)

=> IH=IK.

Xét đường tròn tâm (O), ta có: OK ⊥ CD nên suy ra CK=KD( định lý về đường kính và dây) (1)

Xét đường tròn tâm (O), ta có: OH ⊥ AB nên suy ra AH=HB (định lý về đường kính và dây) (2)

Từ (1) và (2) ta có: CK=AH

Mặt khác, IH=IK

Suy ra AI=CI

Vì CD=AB, mà AI=CI(chứng minh trên) nên ta suy ra ID=IB.

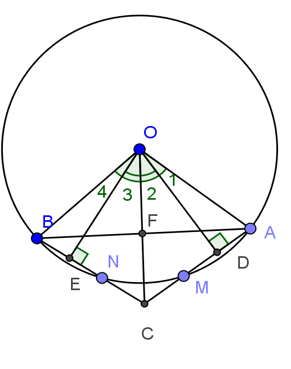
Bài 4: Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM=BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:

a, OC là tia phân giác của góc AOB.

b, OC vuông góc AB.

Hướng dẫn giải

Xét đường tròn tâm (O) có AM=BN

Từ đó ta suy ra OE=OD (tính chất quan hệ giữa đường kính và dây cung)

Xét tam giác vuông AOD và tam giác vuông BOE có:

OA=OB(cùng bằng bán kính)

OE=OD(chứng minh trên)

=> ΔAOD = ΔBOE (cạnh huyền-cạnh góc vuông)

=> ∠O₁ = ∠O₄ (2 góc tương ứng)(1)

Tương tự ta có: ∠O₂ = ∠O₃ (2)

Ta có: ∠AOC = ∠O₁ + ∠O₂

∠BOC = ∠O₃ + ∠O₄

Từ (1) và (2) ta suy ra ∠AOC= ∠BOC

Suy ra OC là tia phân giác của góc AOB.

Xét tam giác OBF và tam giác OAF có:

∠AOC = ∠BOC (chứng minh trên)

OA=OB

OF: chung

Suy ra ΔOBF = ΔOAF (c-g-c)

=> BF=AF( 2 cạnh tương ứng)

=> OC ⊥ AB