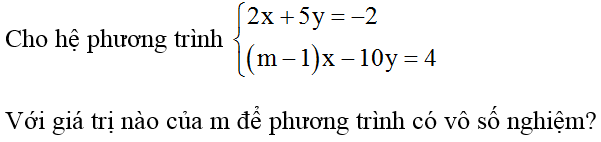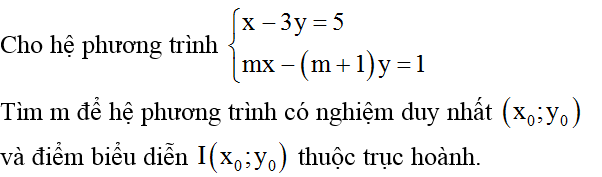Chuyên đề Hệ hai phương trình bậc nhất hai ẩn - Toán lớp 9

---

Chuyên đề Hệ hai phương trình bậc nhất hai ẩn

Với Chuyên đề Hệ hai phương trình bậc nhất hai ẩn Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hệ hai phương trình bậc nhất hai ẩn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

• Công thức nghiệm của phương trình ax+by=c
• Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn
• Bài tập trắc nghiệm Tập nghiệm của hệ phương trình bậc nhất hai ẩn
• Giải hệ phương trình
• Bài tập trắc nghiệm Giải hệ phương trình bằng phương pháp thế
• Bài tập trắc nghiệm Giải hệ phương trình bằng phương pháp cộng đại số
• Giải toán bằng cách lập hệ phương trình
• Ôn tập chương 3

Công thức nghiệm của phương trình ax+by=c

A. Phương pháp giải

Tập nghiệm của phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm.

Tập nghiệm của phương trình được biểu diễn bởi đường thẳng (d) ax + by = c.

B. Bài tập tự luận

Bài 1: Cho phương trình 3x - 2y = 1

a) Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm trên mặt phẳng tọa độ.

b) Tìm nghiệm của phương trình.

Hướng dẫn giải

Bài 2: Xác định phương trình bậc nhất hai ẩn có các nghiệm là (1;-3) và (-2;0). Viết công thức nghiệm tổng quát của phương trình đó.

Hướng dẫn giải

Xét phương trình bậc nhất hai ẩn có dạng tổng quát ax + by = c (a ≠ 0 hoặc b ≠ 0)

+ Thay x = 1; y = -3 và phương trình ta có: a – 3b = c (1)

+ Thay x = -2; y = 0 vào phương trình ta có: -2a = c (2)

Thay (2) vào (1) ta được a - 3b = -2a ⇔ 3a = 3b ⇔ a = b.

Khi đó phương trình có dạng ax + ay = -2a ⇔ x + y = -2 (do a ≠ 0).

Công thức nghiệm tổng quát của phương trình là x ∈ R và y= -x - 2 hoặc x= -y - 2 và y ∈ R

Bài 3: Viết công thức nghiệm của các phương trình sau và biểu diễn tập nghiệm trên mặt phẳng tọa độ.

a) 3x - y = 1/2

b) x + 5y = 0

Hướng dẫn giải

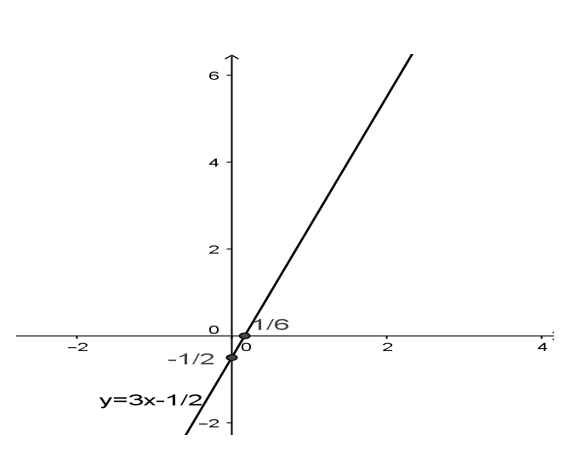
a) 3x - y = 1/2

Công thức nghiệm tổng quát của phương trình là:

x ∈ R; y = 3x - 1/2

Biểu diễn hình học:

x	0	1/6
y	-1/2	0

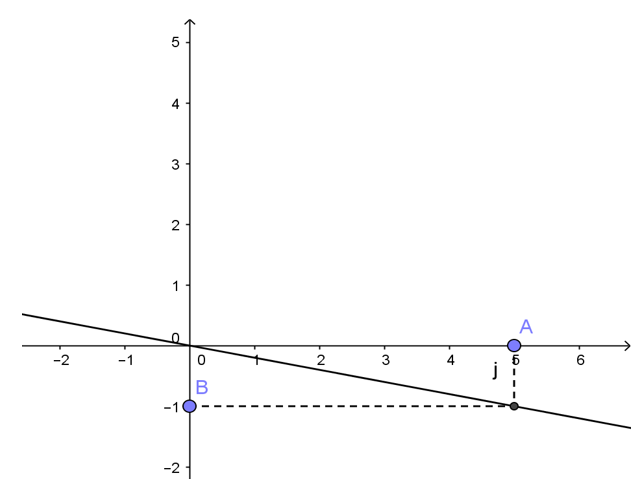
b) x + 5y = 0

Công thức nghiệm tổng quát của phương trình là:

x ∈ R; y = -x/5

Biểu diễn hình học

x	0	5
y	0	-1

Bài 4: Tìm nghiệm nguyên của các phương trình sau:

a) x + 3y = 1

b) 4x - 5y = 24

Hướng dẫn giải

Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn

A. Phương pháp giải

1. Khái niệm về hệ hai phương trình bậc nhất hai ẩn

Trong đó a, b, c, a’, b’, c’ là các số cho trước, x và y gọi là ẩn số.

Nếu hai phương trình (1) và (2) có nghiệm chung thì gọi là nghiệm của hệ phương trình. Hệ phương trình vô nghiệm nếu hai phương trình (1) và (2) không có nghiệm chung.

Giải hệ phương trình là tìm tất cả các nghiệm của nó.

Hai hệ phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm (có thể cùng vô nghiệm).

2. Minh họa hình học tập nghiệm của hệ phương trình bậc nhất hai ẩn

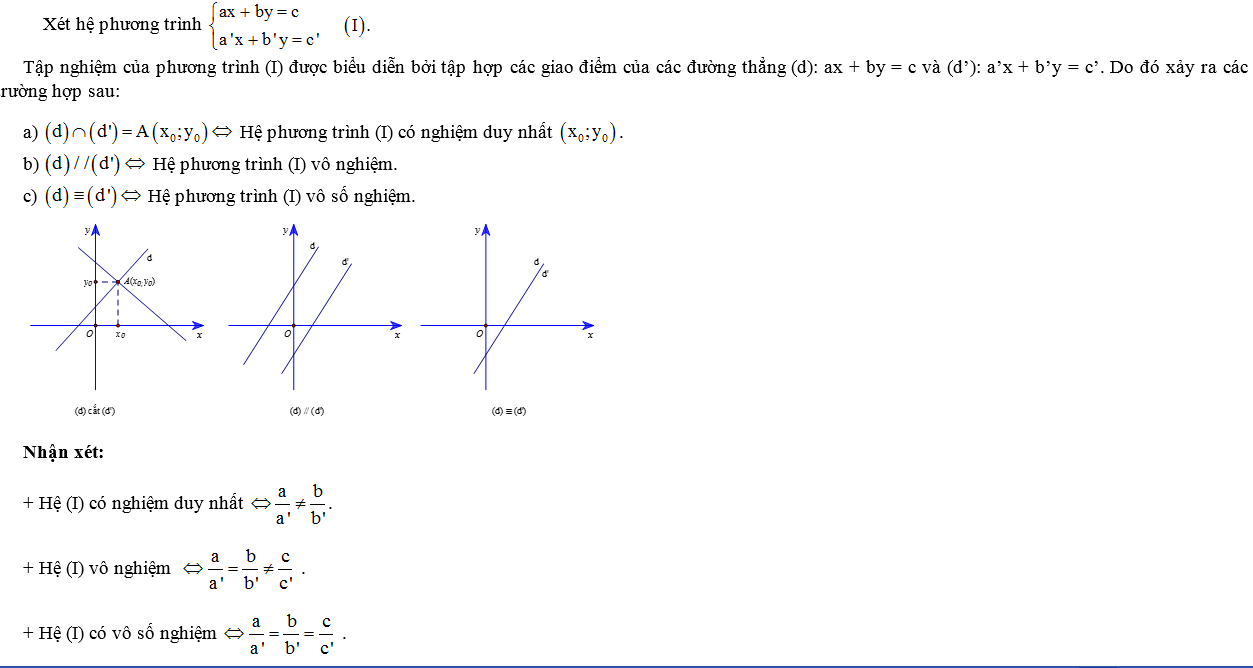
B. Bài tập tự luận

Bài 1: Dựa vào các hệ số a, b, c, a’, b’, c; dự đoán số nghiệm của các phương trình sau:

Hướng dẫn giải

Bài 2: Tìm m để các đường thẳng sau đồng quy:

(d1): 2x + 0y = -4

(d2): 3x + 2y = 6

(d3): mx + (2m - 1)y = 4

Hướng dẫn giải

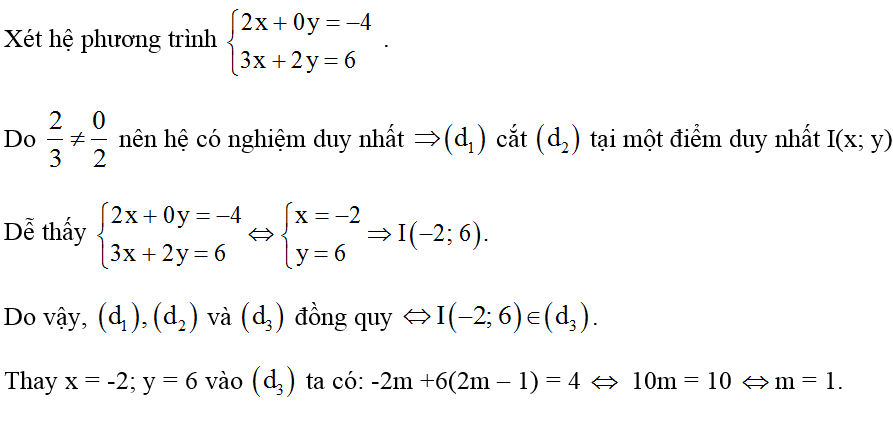
Bài 3:

Hướng dẫn giải

Bài 4: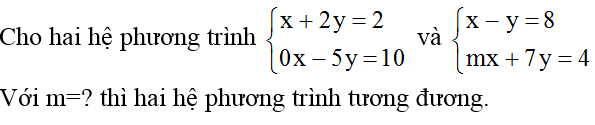

Hướng dẫn giải

Bài 5:

Hướng dẫn giải

Bài 6: Cho phương trình: 3x – 4y = 5.

Hãy viết thêm một phương trình bậc nhất hai ẩn để có được một hệ phương trình:

a) Có nghiệm duy nhất.

b) Vô nghiệm.

c) Có vô số nghiệm.

Hướng dẫn giải

a) Để hệ có nghiệm duy nhất thì 3/a ≠ -4/b => 3b ≠ -4a

Ví dụ phương trình cần tìm là 3x + 5y = 1

b) Để hệ vô nghiệm thì 3/a = -4/b ≠ 5/c

Ví dụ lấy a=3; b=-4; c=10. Khi đó ta được phương trình 3x - 4y = 10

c) Để hệ có vô số nghiệm thì 3/a = -4/b = 5/c

Ví dụ lấy a = 6; b = -8; c = 10 ta được phương trình 6x - 8y = 10

Bài tập trắc nghiệm Tập nghiệm của hệ phương trình bậc nhất hai ẩn

Câu 1: Hệ phương trình 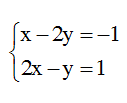có mấy nghiệm?

A. Vô nghiệm

B. Có 1 nghiệm

C. Có vô số nghiệm

Câu 2: “ Hệ hai phương trình bậc nhất hai ẩn vô nghiệm thì luôn tương đương nhau” Câu nói trên đúng hay sai?

A. Sai    B. Đúng

Câu 3: Chọn đáp án đúng.

Công thức nghiệm tổng quá của phương trình 4x – 3y = 11 là:

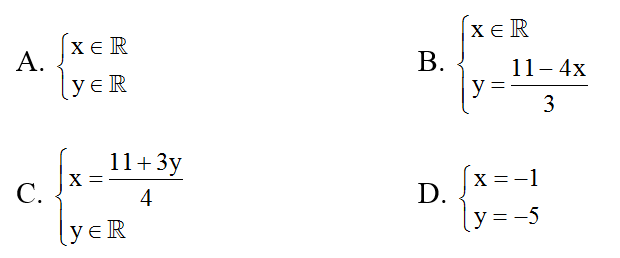
Câu 4: Xác định các hệ số của a, b, c của phương trình ax + by = c biết rằng đường thẳng biểu diễn nghiệm của nó là đường phân giác của góc phần tư thứ nhất.

A. a = -1; b = -1và c = 1    C. a = 1; b = 0 và c = -1

B. a = 1; b = -1 và c = 0    D. a = 0; b = -1 và c = 1

Câu 5: Đường thẳng song song với trục hoành có phương trình dạng nào sau đây (với )?

A. 0x + y = c    B. x + 0y = c

C. x + 0y = c    D. x + y = c

Câu 6: Nghiệm tổng quát của phương trình: 2x-3y=1 là:

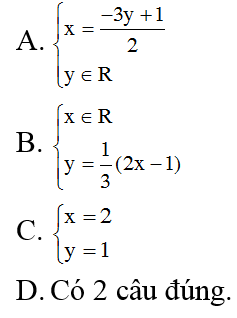
Hướng dẫn giải và đáp án

Câu 1: A

Câu 2: B

Câu 3: C

Câu 4: B

Câu 5: A

Câu 6: D