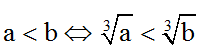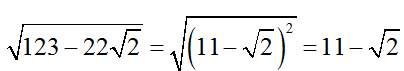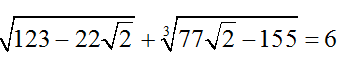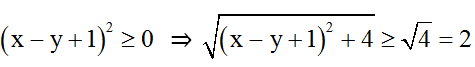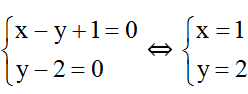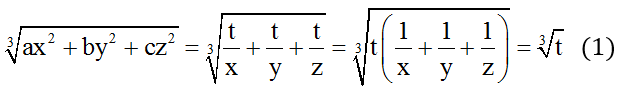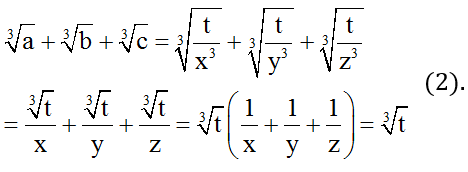Bài toán so sánh, tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa căn thức - Toán lớp 9
Bài toán so sánh, tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa căn thức
Với Bài toán so sánh, tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa căn thức Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập so sánh, tìm giá trị lớn nhất, nhỏ nhất của biểu thức chứa căn thức từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
Phương pháp giải
+ Với hai số thực a, b bất kì ta luôn có: 
+ Với hai số dương a,b bất kì ta có: a < b ⇔ √a < √b .
+ A2 ≥ 0 với mọi biểu thức A.
Ví dụ minh họa
Ví dụ 1: So sánh:
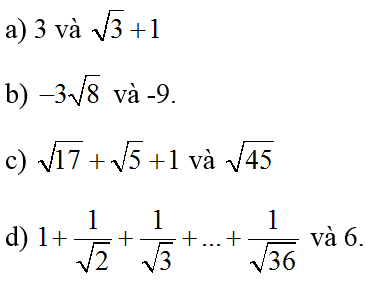
Hướng dẫn giải:
a) Ta có: 3 < 4, suy ra √3 < √4 = 2
Vậy √3 + 1 < 2 + 1 hay √3 + 1 < 3.
b) Ta có: 8 < 9, suy ra √8 < √9 = 3
suy ra 3√8 < 3.3 = 9
suy ra -3√8 > -9
Vậy -3√8 > -9
c) Ta có: 17 > 16, suy ra √17 > √16 = 4
5 > 4, suy ra √5 > √4 = 2
Vậy √17 + √5 + 1 > 4 + 2 + 1 = 7
Mà √45 < √49 = 7
Do đó : √17 + √5 + 1 > √45
d) Ta có : √1 < √36 nên 1 > 1/√36
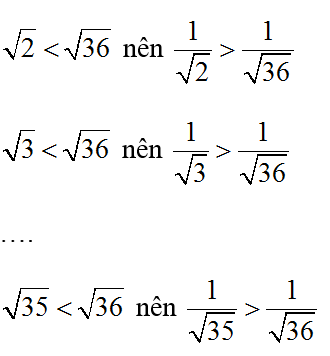
Do đó :
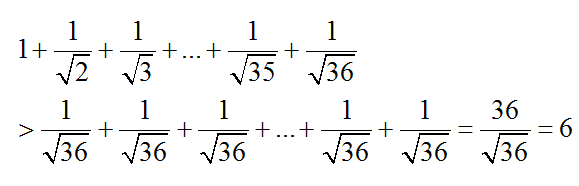
Ví dụ 2: Tìm giá trị nhỏ nhất của biểu thức :
a) x + √x + 1 với x ≥ 0.
b) x - 2√(x-1) với x ≥ 1.
Hướng dẫn giải:
a) Ta có với mọi x ≥ 0 thì √x ≥ 0
⇒ x + √x + 1 ≥ 0 + 0 + 1 = 1.
Dấu "=" khi x = 0.
Vậy Min (x + √x + 1) = 1 đạt được khi x = 0.
b)
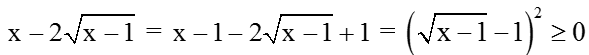
Dấu "=" khi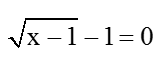 
⇔ x – 1 = 1 ⇔ x = 2.
Vậy Min (x - 2√(x-1)) = 0 đạt được khi x = 2.
Ví dụ 3: Chứng minh các biểu thức sau không phụ thuộc vào biến:
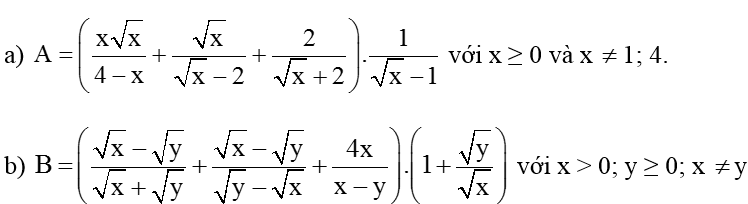
Hướng dẫn giải:
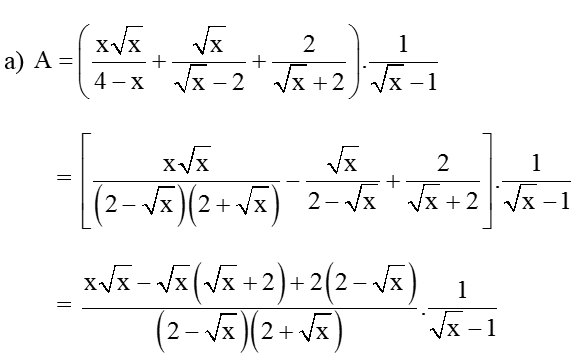
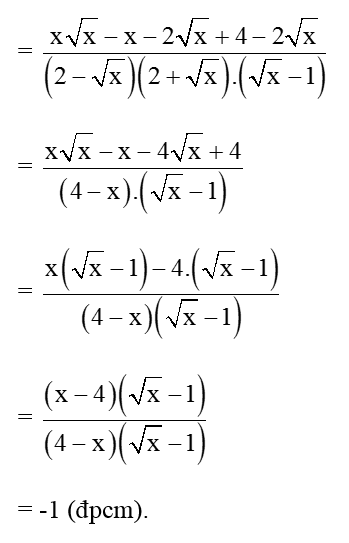
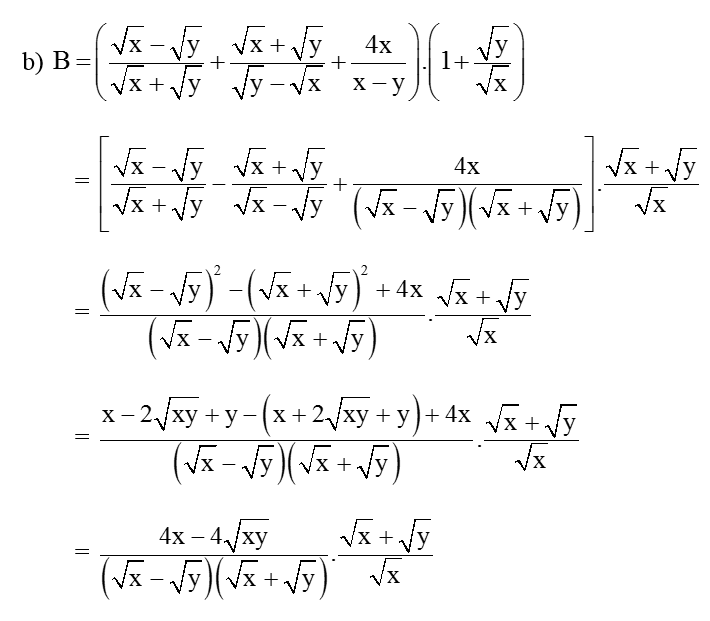
= 4
Bài tập trắc nghiệm tự luyện
Bài 1: Với hai số thực a < b, khẳng định nào dưới đây là đúng ?
Lời giải:
Đáp án: B
Bài 2: Giá trị nhỏ nhất của biểu thức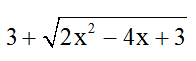 
là :
A. 3 B. 4
C. 2 D. 5.
Lời giải:
Đáp án: B
Bài 3: Giá trị lớn nhất của biểu thức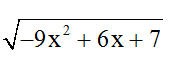 
là :
A. 3 B. 2
C. 2√2 D. 3√2
Lời giải:
Đáp án: C
Bài 4: So sánh nào dưới đây là đúng ?
Lời giải:
Đáp án: B
Bài 5: Với mọi số nguyên dương n, so sánh :
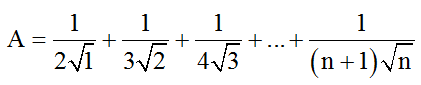
với 2 ta được :
A. A > 2 B. A < 2
C. A = 2 D. không so sánh được
Lời giải:
Đáp án: B
Bài 6: So sánh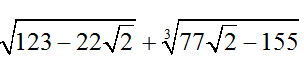 
và 6.
Hướng dẫn giải:
Ta có: 
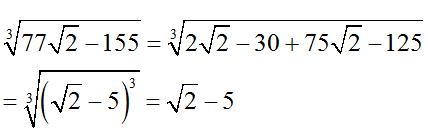
Do đó:
Bài 7: Tìm giá trị nhỏ nhất của các biểu thức sau :
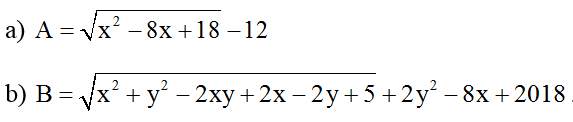
Hướng dẫn giải:
a) Đkxđ : ∀ x ∈ R.
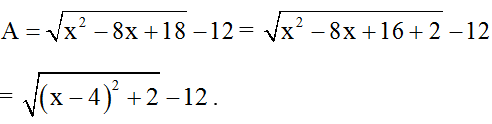
Ta có: (x-4)2 + 2 ≥ 2
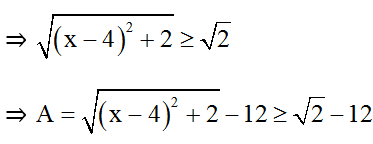
Dấu “=” khi x - 4 = 0 ⇔ x = 4.
Vậy Min A = √2 - 12 xảy ra khi x = 4.
b) Đkxđ: ∀x, y ∈ R.
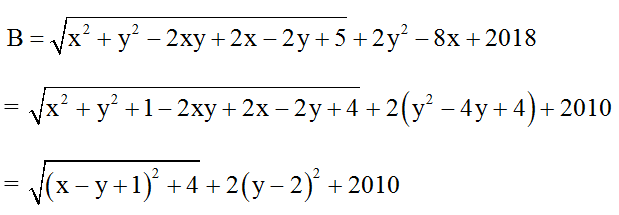
Ta có: 
(y-2)2 ≥ 0
⇒ 
≥ 2 + 0 + 2010 = 2012
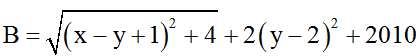
Dấu “=” khi 
Vậy Min B = 2012 đạt được khi x = 1; y = 2.
Bài 8: Chứng minh biểu thức :
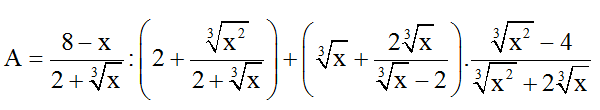
với x ≠ ±8; x ≠ 0 không phụ thuộc vào giá trị của x.
Hướng dẫn giải:
Đặt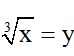 
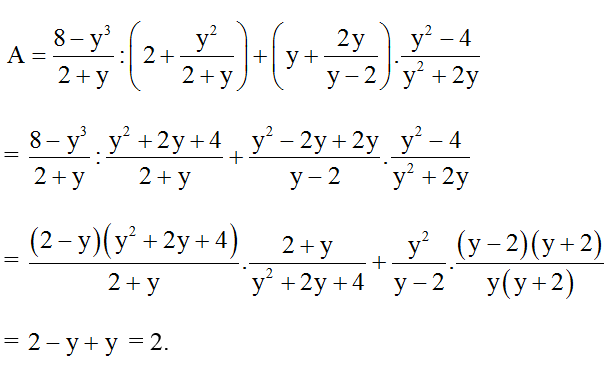
, biểu thức trở thành:
= 2 - y + y = 2.
Vậy giá trị biểu thức không phụ thuộc vào biến.
Bài 9: Chứng minh rằng, nếu :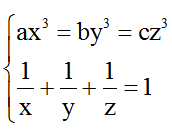 
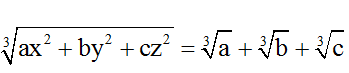
thì : 
Hướng dẫn giải:
Đặt ax3 = by3 = cz3 = t
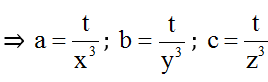
Ta có: 
Mặt khác: 
Từ (1) và (2) suy ra đpcm.
Bài 10: Cho biểu thức Sn = (2-√3)n + (2+√3)n (với n nguyên dương).
a) Chứng minh S3n + 3Sn = Sn3.
b) Tính S3, S9 .
Hướng dẫn giải:
a) Ta có: Sn3 - 3Sn
= [(2-√3) + (2+√3)n]3 - 3. [(2-√3) + (2+√3)n]
= (2-√3)3n + (2+√3)3n + 3.(2-√3)n (2+√3)n. [(2-√3) + (2+√3)n] - 3.[(2-√3) + (2+√3)n]
= (2-√3)3n + (2+√3)3n + 3.[(2-√3)n +(2+√3)n]- 3.[(2-√3)n + (2+√3)n]
(Vì (2-√3)n (2+√3)n = [(2-√3) (2 +√3)]n = 1 ).
= (2-√3)3n + (2+√3)3n = S3n (đpcm).
2. Ta có: S1 = (2-√3)1 + (2+√3)1 = 4
S3 = S13 - 3S1 = 43 - 3.4 = 52
S9 = S33 - 3S3 = 523 - 3.52 = 140452
