Diện tích hình tròn - Toán lớp 9

Diện tích hình tròn

Với Diện tích hình tròn Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Diện tích hình tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

1. Diện tích S của một hình tròn bán kính R được tính theo công thức: S= πR²

2. Hình quạt tròn là một phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai mút của cung đó. Diện tích hình quạt tròn bán kính R, cung n^o được tính theo công thức

S= πR²n / 360 hay S = l.R/2 (l là độ dài cung n^o của hình quạt tròn)

3. Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy.

Diện tích hình viên phân bằng hiệu (hoặc tổng) diện tích của một hình quạt tròn và diện tích của một tam giác nếu góc ở tâm hình quạt nhỏ hơn 180^o (hoặc lớn hơn 180^o) .

4. Hình vành khăn là phần hình tròn giới hạn bởi đường tròn đồng tâm

Diện tích hình vành khăn tạo bởi hai đường tròn đồng tâm bán kính R₁ và R₂ là: S =π(R₁² - R₂²) .

B. Bài tập tự luận

Bài 1: Tính diện tích hình tròn (O) ngoại tiếp tam giác ABC đều cạnh a.

Hướng dẫn giải

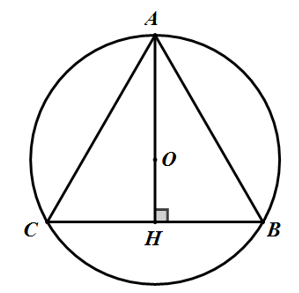
Nối AO cắt BC tại H

Vì O là tâm đường tròn ngoại tiếp tam giác đều ABC nên O đồng thời là trực tâm, trọng tâm của tam giác ABC. Do đó:

AH ⊥ BC và HB = HC = BC/2 = a/2

Xét tam giác vuông ABH vuông tại H có:

AH² = AB² - BH² = a² - (a/2)² = 3a² /4

=> AH = a√3 /2

Do O là trọng tâm tam giác ABC nên:

AO = 2/3 AH = 2/3 . a√3 /2 = a√3 /3

Vậy diện tích hình tròn (O) là:

S= πR² = π(a√3/3)² = πa²/3 (đvdt)

Bài 2: Một hình vuông và một hình tròn có diện tích bằng nhau. Hỏi hình nào có chu vi lớn hơn?

Hướng dẫn giải

Giả sử hình vuông có cạnh a và hình tròn có bán kính R.

Vì hình vuông và hình tròn có diện tích bằng nhau nên ta có:

a² = πR² ⇔ a =R√π

Mặt khác: Chu vi hình vuông là C₁ = 4a = 4R√π

Chu vi hình tròn là C₂ = 2πR

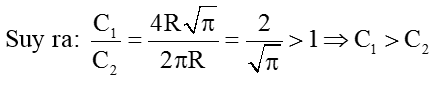
Vậy hình vuông có chu vi lớn hơn.

Bài 3: Cho tam giác ABC đều có tâm O, cạnh 6cm. Vẽ đường tròn (O;2cm). Tính diện tích của phần tam giác nằm ngoài hình tròn (O).

Hướng dẫn giải

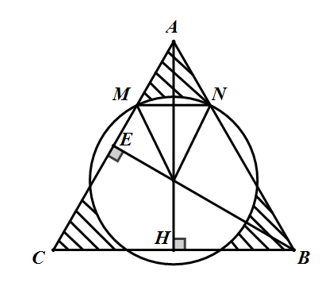
Gọi diện tích phần phải tính (phần gạch sọc trên hình vẽ) là S thì:

S = 3(S_AMON - S_{Quạt tròn OMN})

Giả sử giao điểm của đường tròn (O; 2cm) với hai cạnh AB, AC lần lượt là M và N.

Nối CO cắt AB tại E => CE là đường cao của tam giác đều ABC cạnh 6cm nên:

CE = 6√3 /2 = 3√3 (cm)

Xét tam giác OEM vuông tại E nên:

EM² = OM² - OE² = 2² - (√)² = 1 (cm)

=> EM = 1(cm) => AM = 2EM = 2cm = AN

Dễ thấy tứ giác AMON là hình thoi có OA = OC = 2√3 (cm) và MN = 2cm (do tam giác MON đều) nên:

S_AMOC = AO.MN/2 = 2√3 (cm²)

Diện tích hình quạt tròn OMN là:

S_{quạt tròn OMN} = πR²n /360 = 2π/3 (cm²)

Do diện tích tam giác cong AMN là:

S_AMN = S_AMON - S_{quạt tròn OMN} = 2√3 - 2π/3 (cm²)

Vậy diện tích phần tam giác nằm ngoài hình tròn là:

S = 3(2√3 - 2π/3) = 2(3√3 - π) ≈ 4,1 (cm²)