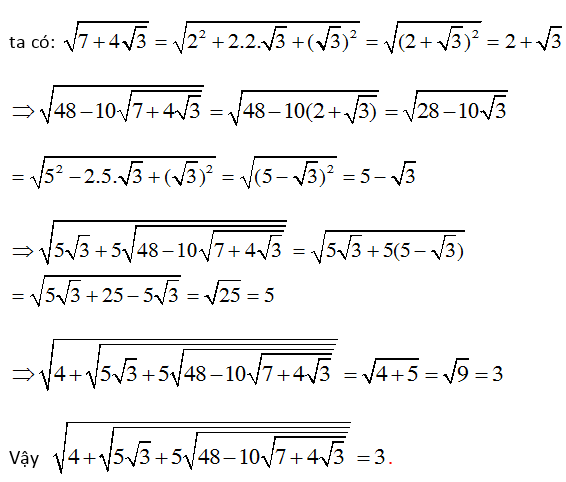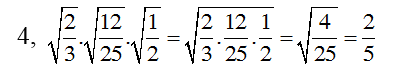Biến đổi căn thức bậc hai đơn giản - Toán lớp 9

Biến đổi căn thức bậc hai đơn giản

Với Biến đổi căn thức bậc hai đơn giản Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Biến đổi căn thức bậc hai đơn giản từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Dựa vào quy tắc nhân các căn bậc hai:

- Với a,b ≥ 0 thì √a . √b = √ab .

- Với a ≥ 0, b≥ 0 thì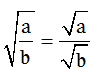

Sau đó thực hiện các phép biến đổi đơn giản biểu thức chứa căn rồi thu gọn các căn thức đồng dạng hoặc rút gọn.

B. Bài tập tự luận

Bài 1: Đưa thừa số vào trong dấu căn

a, 3√5

b, 2/7√35

c, -4√(1/8)

d, -0,06√250

e, x√x

f, y√(x/y)

Hướng dẫn giải

a. 3√5 = √(3².5) = √45

b. 2/7√35 = √((2/7)². 35)= √20/7

c. -4√(1/8) = -√(4².1/8) = -√2

d. -0,06√250 = -√(0,06)².250 = -√0,9

e. x√x = √(x².x) = √x³

f. y√(x/y) = √y².(x/y)= √(xy)

Bài 2: Thực hiện phép tính

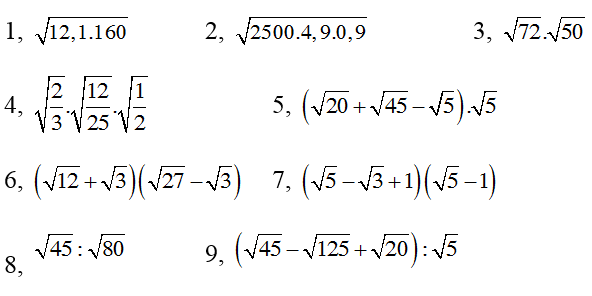
Hướng dẫn giải

1. √(12,1. 160) = √12,1 . √160 = √121 . √16 = 11 . 4 = 44

2. √(2500.4,9.0,9) = √(25.49.9) = √25 . √49 √9 = 5 .7 . 3 = 105

3. √72 . √50 = √(72.50) = √(36.100) = √36 . √100 = 6.10 =60

5. (√20 + √45 - √5)√5 = √100 + √225 - √25 = 10 + 15 - 5 = 20

6. (√12 + √3)(√27 - √3) = √324 - √36 + √81 -√9 = 18 - 6 + 9 - 3 = 18

7. (√5 - √3 + 1)(√5 - 1) = 5 - √5 - √15 +√3 + √5 - 1 = 4 - √15 + √3

8. √45 : √80 = √(45/80) = √(9/16) = √(3/4)

9. (√45 - √125 + √20) : √5 = √9 - √25 + √4 = 3 - 5 + 2 = 0

Bài 3: Thực hiện phép tính sau:

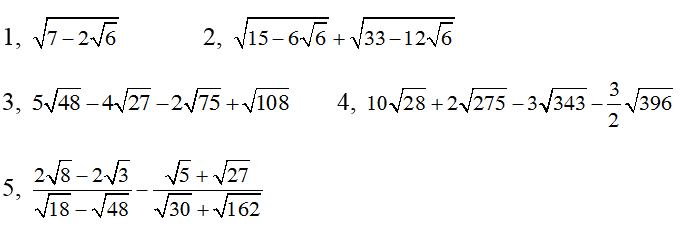
Hướng dẫn giải

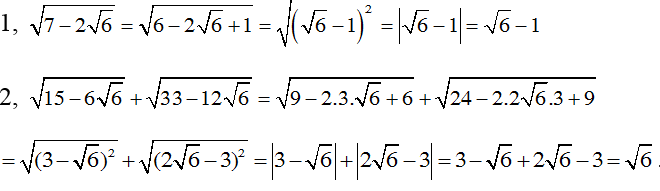
3. 5√48 - 4√27 - 2√75 + √108 = 5√(4².3) - 4√(3².3) - 2√(5².3) + √(6².3)

= 20√3 - 12√3 - 10√3 + 6√3 = 4√3

4. 10√28 + 2√275 - 3√343 - 3/2√396

= 10√(4.7) + 2√(11.25) - 3√(7³) - 3/2√(36.11)

= 20√7 + 10√11 - 21√7 -3/2.6√11

= √11 - √7

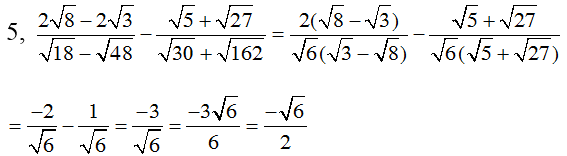
Bài 4: Thực hiện phép tính

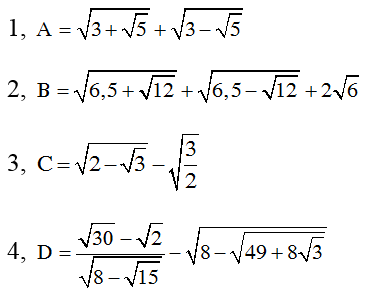
Hướng dẫn giải

1.

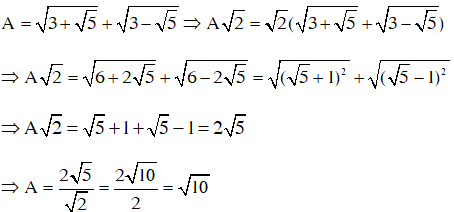
2.

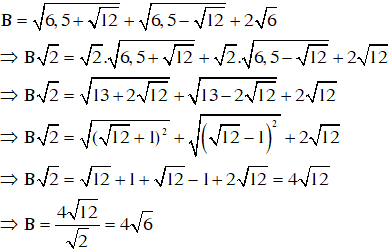
3.

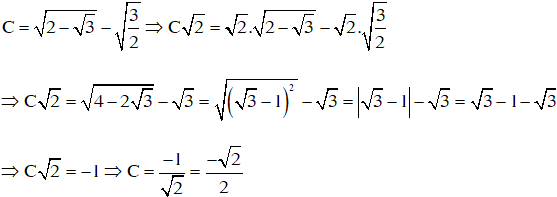
4.

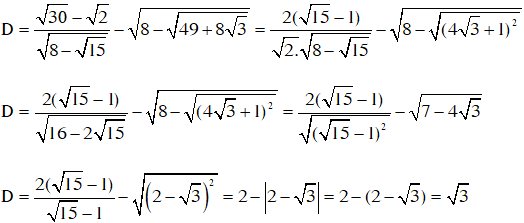
Bài 5: Rút gọn biểu thức sau

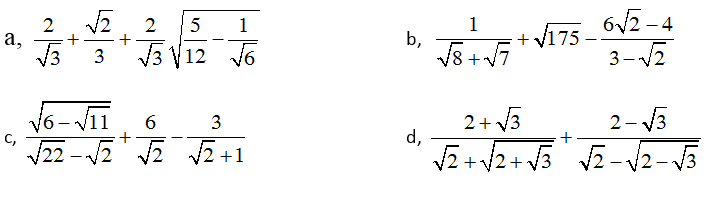
Hướng dẫn giải

a.

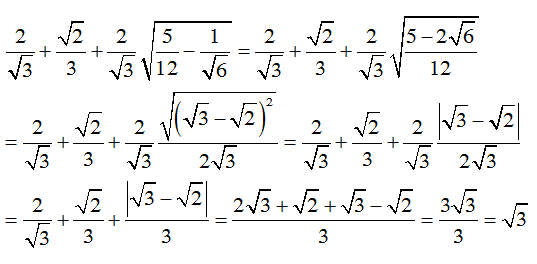
b.

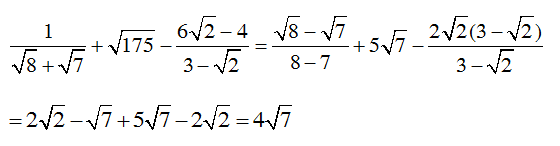
c.

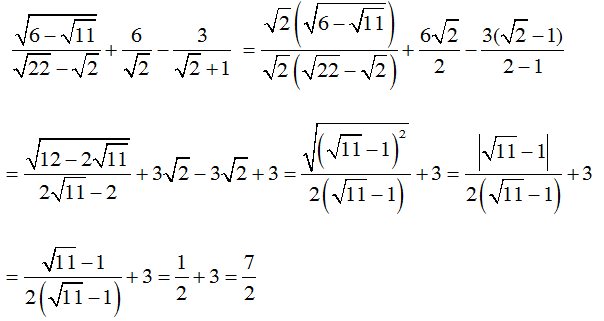
d.

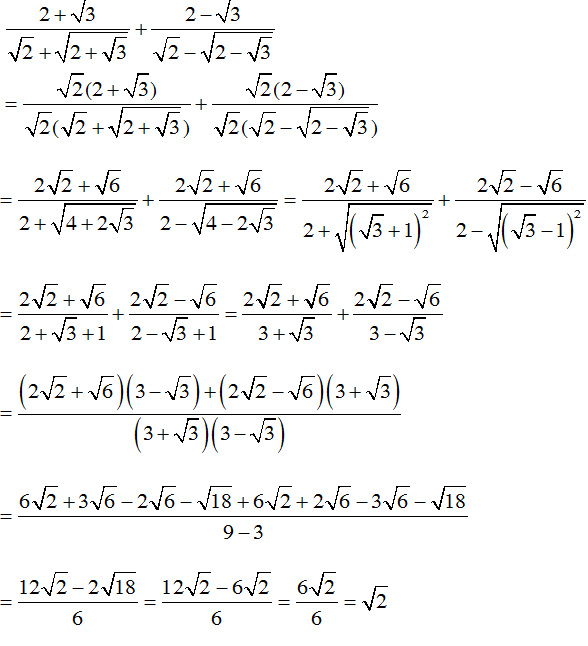
Bài 6: Rút gọn biểu thức sau

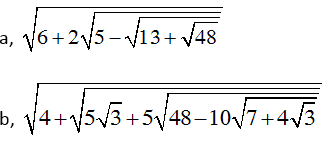
Hướng dẫn giải

a.

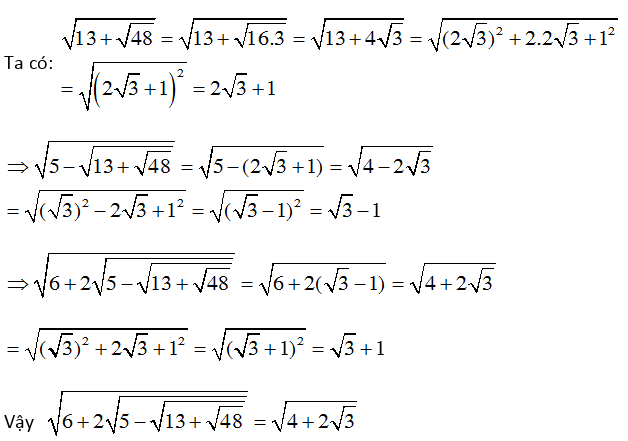
b.