Hình trụ - Hình nón - Hình cầu - Toán lớp 9
Hình trụ - Hình nón - Hình cầu
Với Hình trụ - Hình nón - Hình cầu Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hình trụ - Hình nón - Hình cầu từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải
1. Khái niệm hình trụ
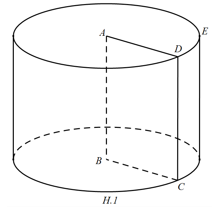
Khi quay hình chữ nhật ABCD một vòng quay cạnh AB cố định ta được 1 hình trụ (H.1)
- AD và BC quét nên hai đáy của hình trụ. HÌnh tròn (A) và (B) bằng nhau và nằm trong hai mặt phẳng song song.
- DC quét nên mặt xung quanh của hình trụ, DC và EF là hai đường sinh. Độ dài đường sinh là chiều cao của hình trụ.
2. Công thức
(R là bán kính đáy, h là chiều cao, S là diện tích đáy).
C. Bài tập tự luận
Bài 1: Một vật thể có dạng hình trụ (H2) bán kính đường tròn đáy và chiều cao của nó đều bằng 2a (cm). Người ta khoan một lỗ cũng có dạng hình trụ có bán kính đáy và độ sâu đều bằng a (cm).
a) Tính thể tích phần vật thể còn lại.
b) Nếu ta sơn cả bên trong lẫn bên ngoài vật thể thì diện tích vật thể được bao phủ là bao nhiêu?
Hướng dẫn giải
a) Gọi thể tích các hình trụ lớn, hình trụ nhỏ lần lượt là V1, V2
Thể tích cần tìm sẽ là:
V = V1 - V2
V = π(2a)2.2a - π.a2.a
= 8πa3 - πa3
= 7πa3 (cm3)
b) Diện tích cần tìm bằng diện tích toàn phần của hình trụ lớn cộng thêm diện tích xung quanh của hình trụ nhỏ:
S = 2π.2a.2a + 2π.(2a)2+ 2π.a.a
= 8πa2 + 8πa2 + 2πa2
= 18πa2 (cm2)

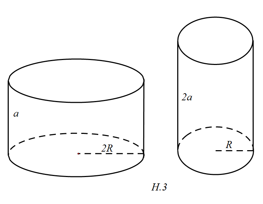
Bài 2: Có 2 lọ có dạng hình trụ, các kích thước như ở hình 3. Hãy so sánh dung tích của 2 lọ và diện tích xung quanh của 2 lọ.
Hướng dẫn giải
a) V1 = πR2 . 2a = 2πR2a
V2 = π.(2R)2.a = 4πR2a
=>V1 = 2V2
b) S1 = 2πR.2a = 4πR.a
S2 = 2π.2R.a = 4πRa
=> S1 = S2
Bài 3: Cho hình lăng trụ đứng có đáy là lục giác đều cạnh a, chiều cao lăng trụ là h. Xét hai hình trụ, một hình có đáy là hình tròn nội tiếp đáy lăng trụ, một hình có đáy là hình tròn ngoại tiếp đáy lăng trụ. Chiều cao của hai hình trụ này đều bằng chiều cao của hình lăng trụ.
a) Tính Sxq của hai hình trụ đó.
b) Tính tỷ số thể tích, tỷ số Sxq của hai hình trụ.
Tìm sự liên hệ giữa hai tỷ số đó.
Hướng dẫn giải
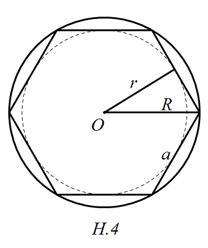
Dễ thấy hình lục giác đều có cạnh a nên:
=> R =a ; r= a√3/2
a) Gọi S1, S2 lần lượt là diện tích xung quanh của hình tròn ngoại tiếp, nội tiếp hình lăng trụ. Ta có:
S1 = 2πRh = 2πah
S2 = 2πrh = πah√3
b) Gọi V1, V2 lần lượt là thể tích của hình trụ ngoại tiếp, nội tiếp hình lăng trụ đó. Ta có:
V1 = πR2h = πa2h
V2 = πr2h = 3πa2h/4