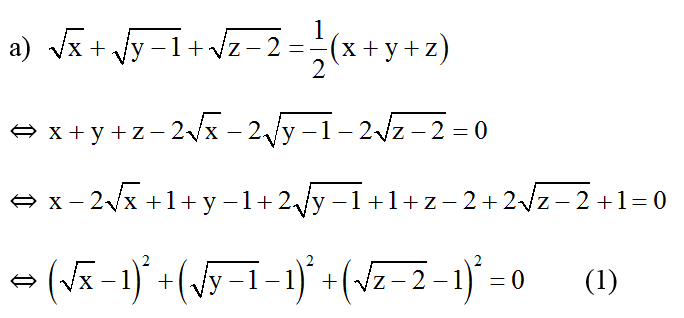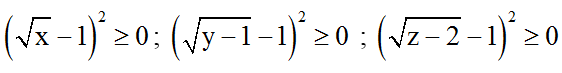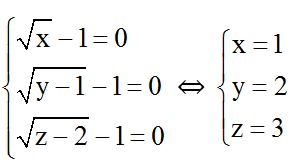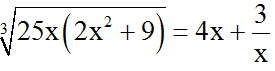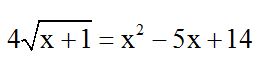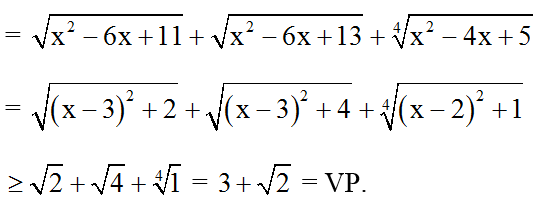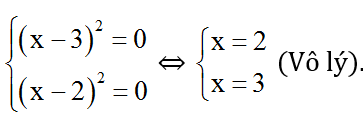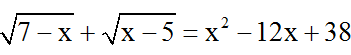Cách giải phương trình vô tỉ bằng phương pháp đánh giá cực hay - Toán lớp 9

---

Cách giải phương trình vô tỉ bằng phương pháp đánh giá cực hay

Với Cách giải phương trình vô tỉ bằng phương pháp đánh giá cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình vô tỉ bằng phương pháp đánh giá từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Phương pháp giải

Bước 1: Tìm đkxđ

Bước 2: Đánh giá một vế lớn hơn hoặc bằng vế còn lại hoặc đánh giá cả hai vế.

+ Cách 1: Đưa 1 vế về dạng A² + B² + C² + ... = 0

Phương trình có nghiệm ⇔ A = B = C = ... = 0.

+ Cách 2 : Sử dụng các BĐT để đánh giá.

BĐT Cô-si áp dụng cho hai số dương : a² + b² ≥ 2ab

BĐT hệ quả : 2(a² + b²) ≥ (a+b)²

BĐT Cô-si áp dụng cho ba số dương : a³ + b³ + c³ ≥ 3abc

...

Bước 3 : Xét dấu = xảy ra và đối chiếu tìm nghiệm của phương trình.

Ví dụ minh họa

Ví dụ 1: Giải phương trình: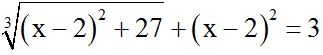

Hướng dẫn giải:

Ta có: (x-2)² ≥ 0

⇒ (x-2)² + 27 ≥ 27

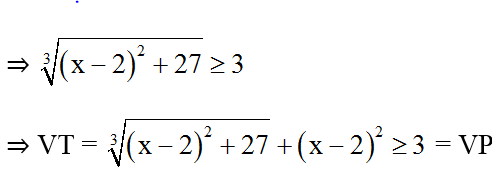
Dấu "=" khi (x – 2)² = 0 ⇔ x = 2.

Vậy phương trình có nghiệm x = 2.

Ví dụ 2: Giải các phương trình sau:

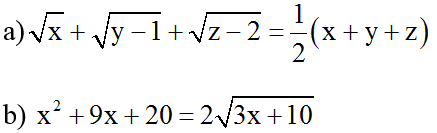
Hướng dẫn giải:

⇔

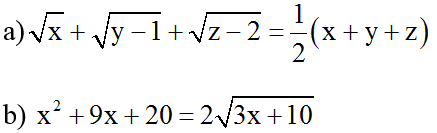Ta có:

Suy ra

Suy ra pt (1) ⇔

Vậy phương trình có nghiệm x = 1; y = 2; z = 3.

Ví dụ 3: Giải phương trình

Hướng dẫn giải:

Đkxđ : x ≠ 0.

Nhân cả hai vế với 3x ta được : 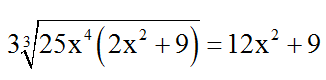(1) .

Ta có :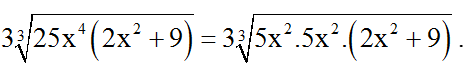

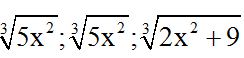
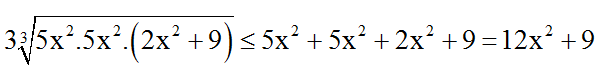
Áp dụng BĐT Cô si cho ba số ta có :

⇒ VT (1) ≤ VP (1).

PT có nghiệm ⇔ 5x² = 2x² + 9 ⇔ 3x² = 9 ⇔ x² = 3 ⇔ x = ±√3 .

Vậy phương trình có 2 nghiệm x = ±√3 .

Bài tập trắc nghiệm tự luyện

Bài 1: BĐT nào dưới đây là đúng với mọi số thực x ?

A. x² + 1 ≥ 2x    B. x³ + 1 ≥ 3x

C. x⁴ + 1 ≥ 4x    D. x⁵ + 1 ≥ 5x

Lời giải:

Đáp án: A

Bài 2: Phương trình 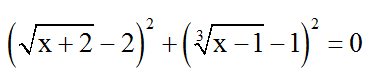có tổng các nghiệm bằng :

A. 0    B. 1

C. 2    D. 3

Lời giải:

Đáp án: C

Bài 3: Đánh giá nào dưới đây là không đúng ?

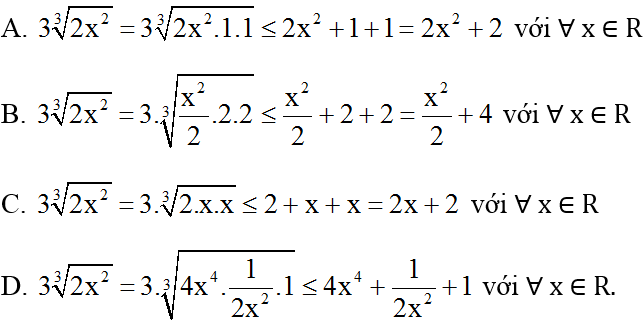
Lời giải:

Đáp án: C

Bài 4: Khẳng định nào dưới đây đúng về phương trình :

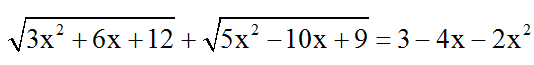
A. Phương trình có một nghiệm âm

B. Phương trình có một nghiệm dương

C. Phương trình có hai nghiệm trái dấu

D. Phương trình vô nghiệm.

Lời giải:

Đáp án: D

Bài 5: Phương trình 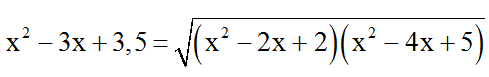có số nghiệm là :

A. 0    B. 1

C. 2    D. 3

Lời giải:

Đáp án: B

Bài 6: Giải phương trình

Hướng dẫn giải:

Đkxđ : x ≥ -1.

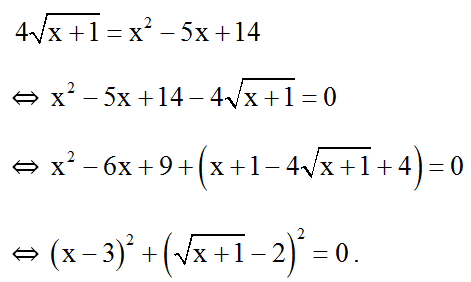
Nhận thấy : VT = 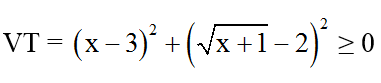với mọi x.

PT có nghiệm ⇔ 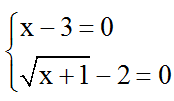⇔ x = 3 (t.m)

Vậy phương trình có nghiệm x = 3.

Bài 7: Giải phương trình: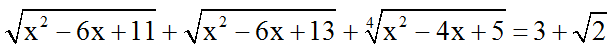

Hướng dẫn giải:

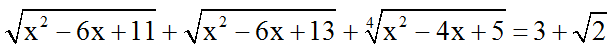
Ta có :

VT

Phương trình có nghiệm ⇔

Vậy phương trình vô nghiệm

Bài 8: Giải phương trình :

Hướng dẫn giải:

Đkxđ : 5 ≤ x ≤ 7 .

+ Áp dụng BĐT : (a + b)² ≤ 2(a² + b²) ta có:

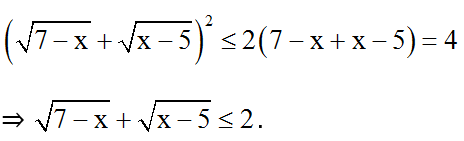
+ x² - 12x + 38 = (x-6)² + 2 ≥ 2

⇒ VT ≤ VP với mọi x.

Phương trình có nghiệm ⇔ 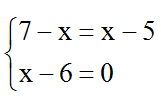⇔ x = 6.

Vậy phương trình có nghiệm x = 6.

Bài 9: Giải phương trình :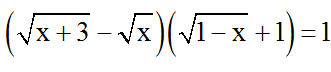

Hướng dẫn giải:

Đkxđ : 0 ≤ x ≤ 1 .

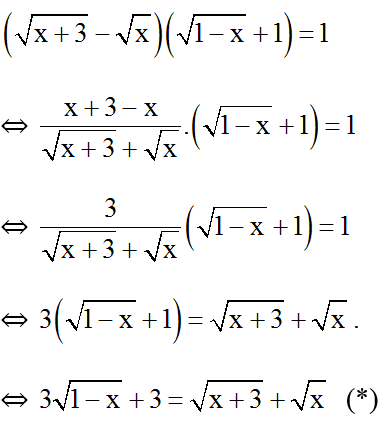
+ Nếu x = 1, VT (*) = 3 ; VP (*) = 3.

⇒ x = 1 là nghiệm của phương trình.

+ Với 0 ≤ x ≤ 1 thì

⇒ Phương trình vô nghiệm.

Vậy phương trình có nghiệm duy nhất x = 1.

Bài 10: Giải phương trình :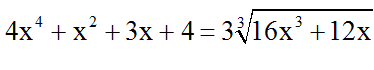

Hướng dẫn giải:

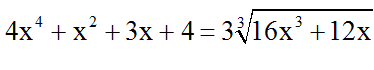
Gợi ý: PT có nghiệm x = 1/2 . Do đó ta thêm bớt các số để đánh giá BĐT sao cho dấu = đều xảy ra tại x = 1/2 .

Giải :

Nhận xét : VT = 4x⁴ + x² + 3x + 4 > 0 với mọi x.

PT có nghiệm ⇔ 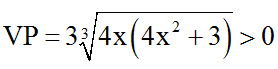⇔ x > 0.

Khi đó áp dụng BĐT Cô-si cho VT ta có :

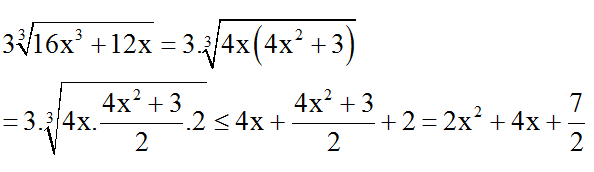
Áp dụng BĐT Cô-si cho vế trái ta được :

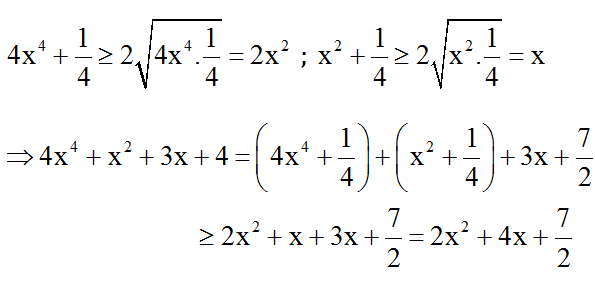
⇒ VT ≥ VP

Phương trình có nghiệm ⇔ x = 2.

Vậy phương trình có nghiệm duy nhất x = 2.