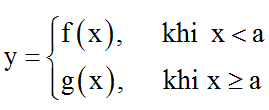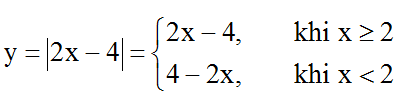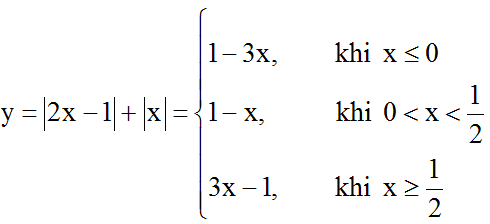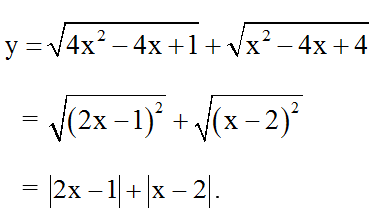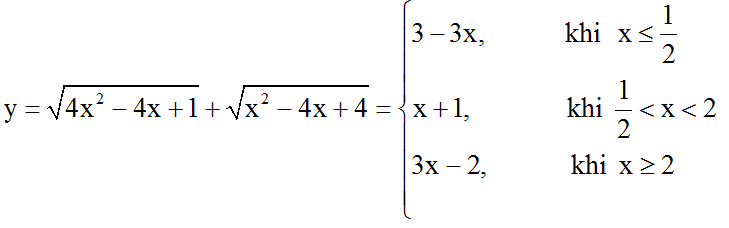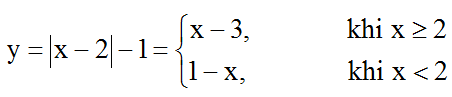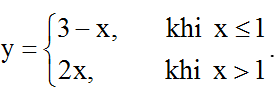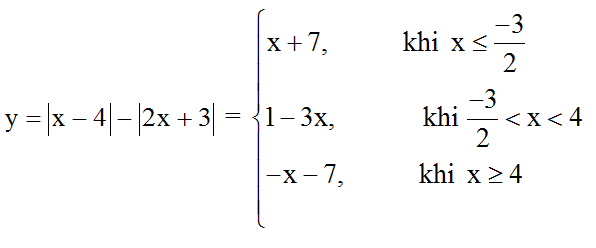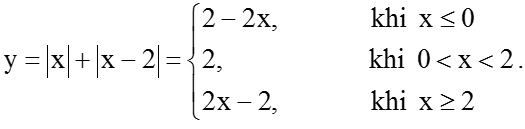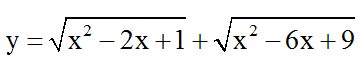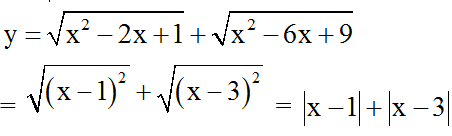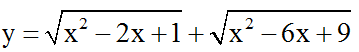Bài toán Đồ thị hàm số trị tuyệt đối cực hay - Toán lớp 9

---

Bài toán Đồ thị hàm số trị tuyệt đối cực hay

Với Bài toán Đồ thị hàm số trị tuyệt đối cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đồ thị hàm số trị tuyệt đối từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Phương pháp giải

+ Cách vẽ đồ thị hàm số y = |f(x)|.

Bước 1: Vẽ đồ thị hàm số y = f(x).

Bước 2: Giữ nguyên phần đồ thị nằm phía trên trục hoành

Bước 3: Lấy đối xứng phần đồ thị phía dưới trục hoành qua trục hoành.

+ Vẽ đồ thị hàm số dạng

Bước 1. Vẽ đồ thị hàm số y = f(x), giữ lại phần có hoành độ nhỏ hơn a.

Bước 2. Vẽ đồ thị hàm số y = g(x), giữ lại phần có hoành độ lớn hơn hoặc bằng a.

+ Biện luận nghiệm phương trình dựa vào đồ thị hàm số.

Số nghiệm của phương trình f(x) = m chính là số giao điểm của đường thẳng y = m và đồ thị hàm số y = f(x).

Ví dụ minh họa

Ví dụ 1: Vẽ đồ thị hàm số y = |2x – 4|.

Hướng dẫn giải:

Ta có:

Đồ thị hàm số y = |2x – 4| được vẽ bằng cách:

+ Vẽ đường thẳng y = 2x – 4

+ Giữ nguyên phần đồ thị nằm phía trên trục hoành

+ Lấy đối xứng phần đồ thị nằm phía dưới trục hoành qua trục hoành.

Ta được đồ thị hàm số như hình vẽ dưới.

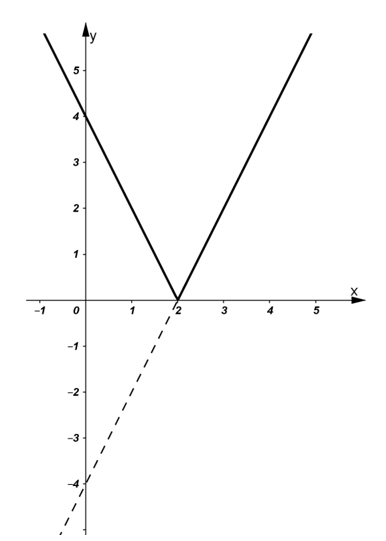
Ví dụ 2: a) Vẽ đồ thị hàm số y = |2x – 1| + |x|.

b) Dựa vào đồ thị tìm giá trị nhỏ nhất của hàm số y = |2x – 1| + |x|

Hướng dẫn giải:

a) Ta có bảng xét giá trị tuyệt đối sau:

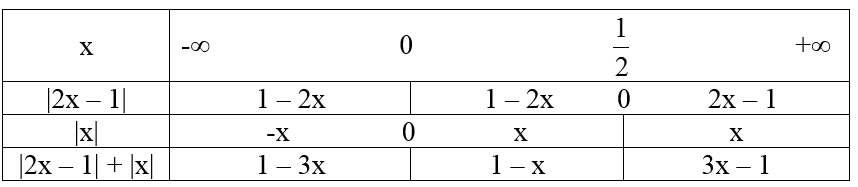
Từ đó suy ra :

Vậy đồ thị của hàm số y = |2x – 1| + |x| gồm ba phần:

+ Đường thẳng y = 1 – 3x chỉ lấy phần đồ thị có hoành độ nhỏ hơn hoặc bằng 0.

+ Đường thẳng y = 1 – x chỉ lấy phần đồ thị có hoành độ lớn hơn 0 và nhỏ hơn 1/2 .

+ Đường thẳng y = 3x – 1 chỉ lấy phần đồ thị có hoành độ lớn hơn hoặc bằng 1/2 .

Ta được đồ thị hàm số y = |2x – 1| + |x| như hình vẽ dưới.

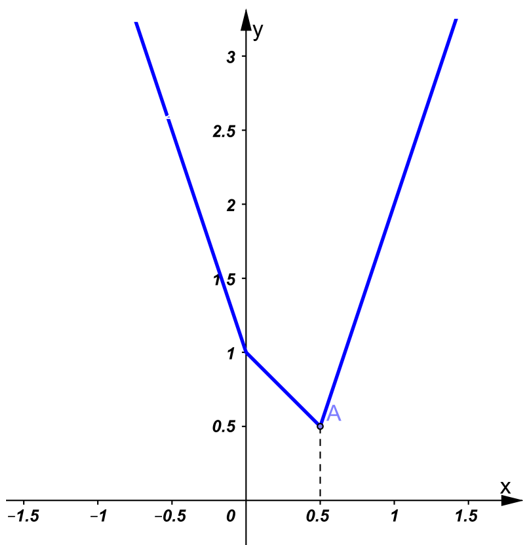
b) Nhìn vào đồ thị ta thấy điểm có tung độ nhỏ nhất thuộc đồ thị hàm số là A(1/2;1/2) .

Vậy hàm số đạt giá trị nhỏ nhất bằng 1/2 , đạt tại x = 1/2 .

Ví dụ 3: a) Vẽ đồ thị hàm số .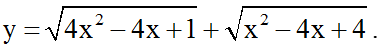

b) Biện luận theo m số nghiệm của phương trình: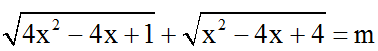

Hướng dẫn giải:

Ta có:

Ta có bảng xét giá trị tuyệt đối sau:

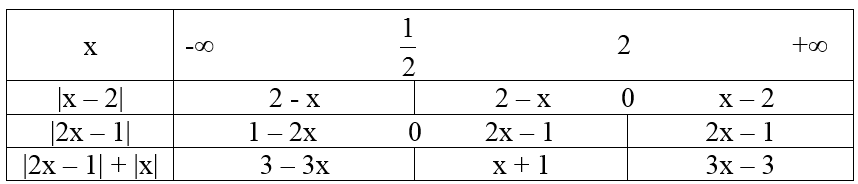
Từ đó suy ra

Vậy đồ thị hàm số gồm ba phần:

+ Một phần đường thẳng y = 3 – 3x lấy phần có hoành độ nhỏ hơn hoặc bằng 1/2

+ Một phần đường thẳng y = x + 1 lấy phần có hoành độ nằm giữa 1/2 và 2.

+ Một phần đường thẳng y = 3x – 2 lấy phần có hoành độ lớn hơn hoặc bằng 2.

Ta có đồ thị hàm số như dưới hình:

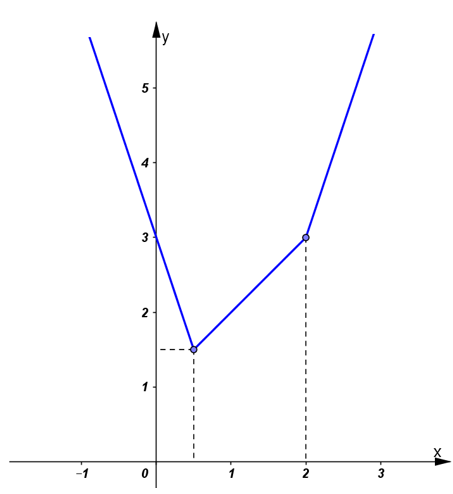
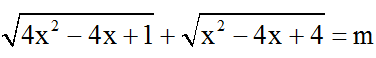
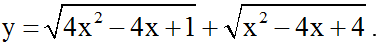
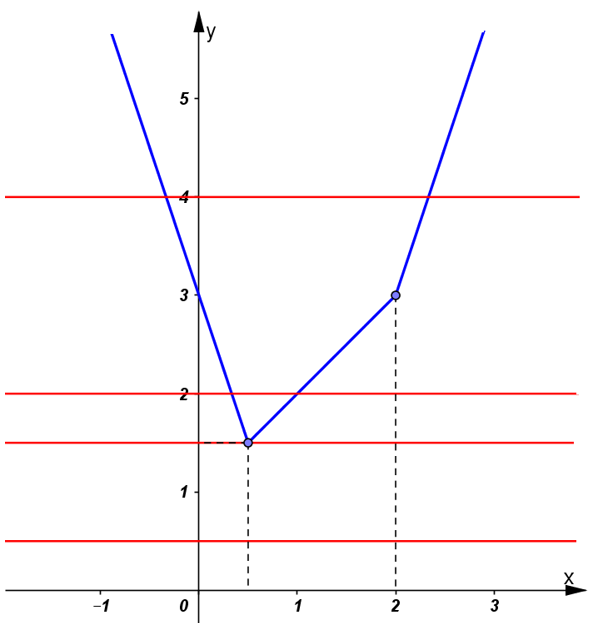
b) Số nghiệm của phương trình (1) phụ thuộc vào số giao điểm của đường thẳng y = m (song song với trục hoành) và đồ thị hàm số .

+ Nếu m < 3/2 , đường thẳng y = m không cắt đồ thị hàm số

⇒ Phương trình vô nghiệm.

+ Nếu m = 3/2 , đường thẳng y = m cắt đồ thị hàm số tại điểm duy nhất (1/2; 3/2)

⇒ Phương trình có nghiệm duy nhất .

+ Nếu m > 3/2 , đường thẳng y = m cắt đồ thị hàm số tại hai điểm pb

⇒ Phương trình có hai nghiệm phân biệt.

Vậy: Với m < 3/2 , phương trình vô nghiệm.

Với m = 3/2 , phương trình có nghiệm duy nhất .

Với m > 3/2 , phương trình có hai nghiệm.

Bài tập trắc nghiệm tự luyện

Bài 1: Hàm số y = |x – 2| có giá trị nhỏ nhất là:

A. 0    B. 2    C. -2     D. -1.

Lời giải:

Đáp án: A

Bài 2: Giá trị của hàm số y = |2x – 3| - |-x + 1| tại x = 0 là:

A. 2    B. 4    C. -2    D. -4.

Lời giải:

Đáp án: A

Bài 3: Đồ thị dưới đây là của hàm số nào?

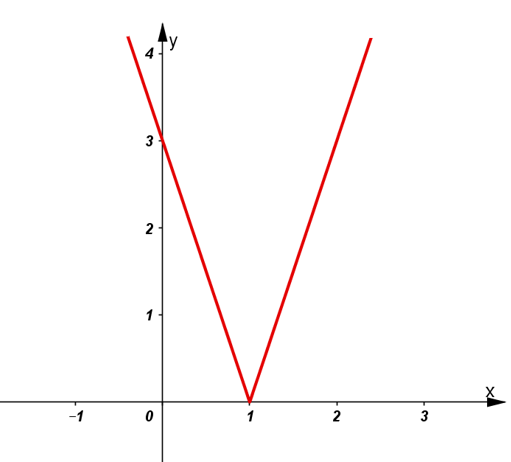
A. y = |3x-3|    B. y = |x-1|

C. y = |3x|    D. y = |x-2| .

Lời giải:

Đáp án: A

Bài 4: Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây:

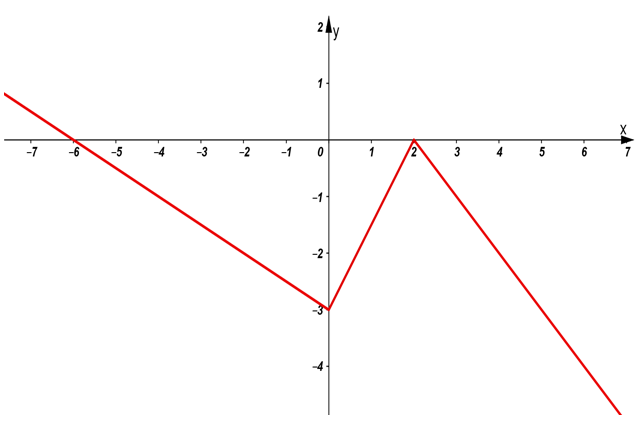
Phương trình f(x) = m có thể có tối đa bao nhiêu nghiệm?

A. 0    B. 1    C. 2    D. 3

Lời giải:

Đáp án: D

Bài 5: Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây:

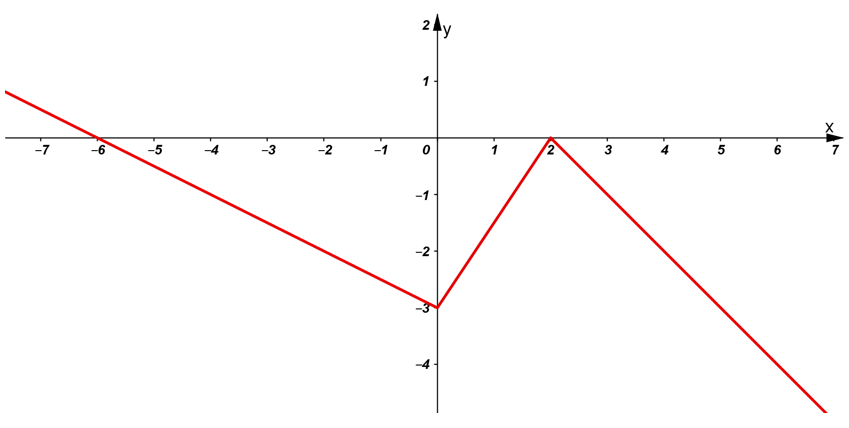
Có bao nhiêu giá trị của m để phương trình f(x) = m có hai nghiệm?

A. 0    B. 1    C. 2    D. 3

Lời giải:

Đáp án: C

Bài tập tự luận tự luyện

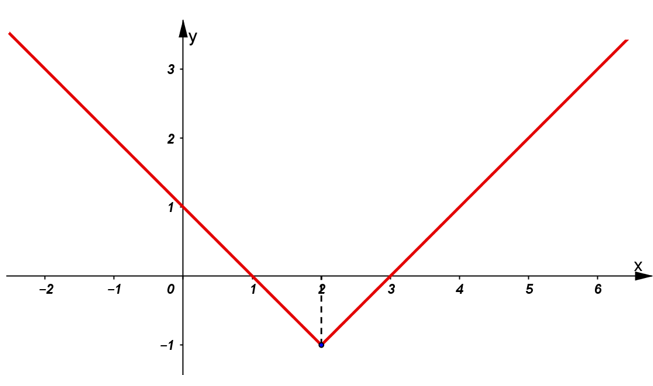
Bài 6: Vẽ đồ thị hàm số y = |x-2| - 1

Hướng dẫn giải:

Ta có:

Từ đó suy ra đồi thị hàm số gồm 2 phần:

+ Một phần đường thẳng y = x – 3 có hoành độ lớn hơn hoặc bằng 2.

+ Một phần đường thẳng y = 1 – x có hoành độ nhỏ hơn 2.

Ta có đồ thị hàm số như hình vẽ dưới:

Bài 7: Vẽ đồ thị hàm số

Xác định giá trị nhỏ nhất của hàm số trên.

Hướng dẫn giải:

Có thể nhận thấy, đồ thị hàm số 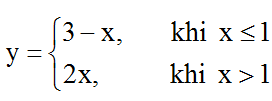gồm hai phần:

+ Phần đường thẳng y = 3 – x với các điểm có hoành độ nhỏ hơn hoặc bằng 1.

+ Phần đường thẳng y = 2x với các điểm có hoành độ lớn hơn 1.

Ta có đồ thị hàm số như hình vẽ dưới:

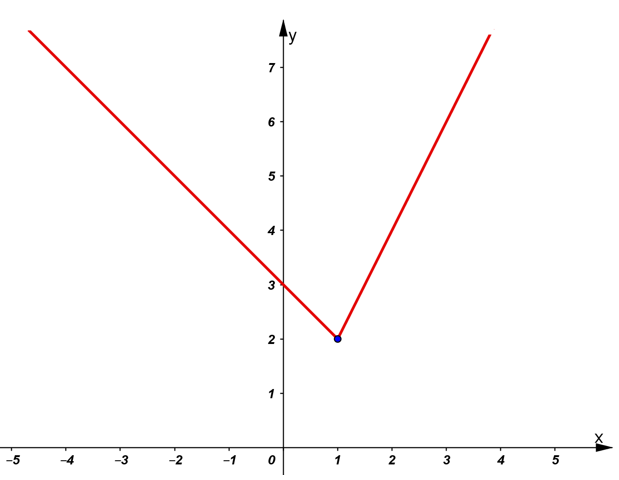
Dựa vào đồ thị hàm số thấy điểm có tung độ nhỏ nhất là (1; 2).

Vậy hàm số đạt giá trị nhỏ nhất bằng 2, khi x = 1.

Bài 8: Tìm m để phương trình |x – 4| - |2x + 3| - m = 0 có hai nghiệm phân biệt.

Hướng dẫn giải:

Xét hàm số y = |x – 4| - |2x + 3|.

Ta có bảng xét giá trị tuyệt đối dưới đây:

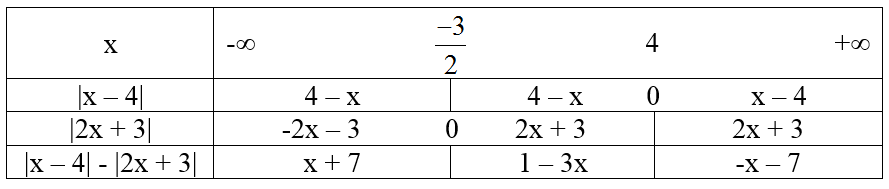
Suy ra:

Vậy đồ thị hàm số gồm ba phần:

+ Phần đường thẳng y = x + 7 lấy các điểm có hoành độ nhỏ hơn hoặc bằng -3/2 .

+ Phần đường thẳng y = 1 – 3x lấy các điểm có hoành độ từ -3/2 đến 4.

+ Phần đường thẳng y = -x – 7 lấy các điểm có hoành độ lớn hơn hoặc bằng 4.

Ta có đồ thị hàm số như hình vẽ dưới :

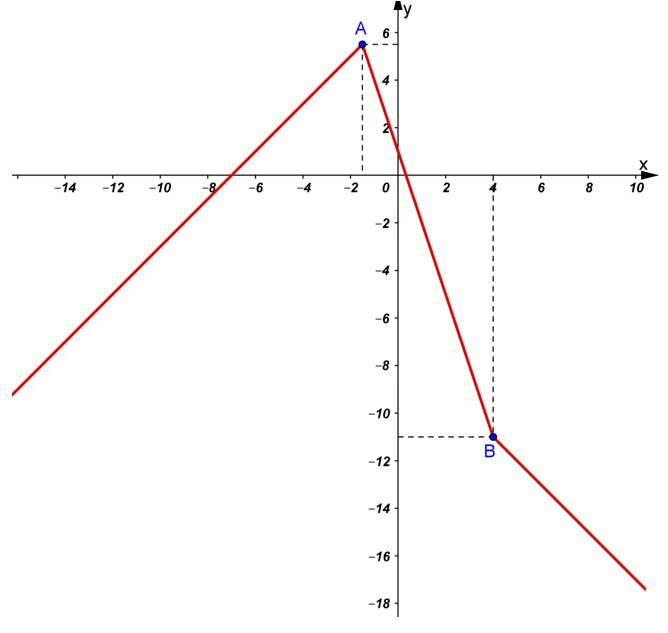
+ Phương trình |x – 4| - |2x + 3| - m = 0 có hai nghiệm phân biệt

⇔ |x – 4| - |2x + 3| = m có hai nghiệm pb

⇔ Đường thẳng y = m cắt đồ thị hàm số y = |x – 4| - |2x + 3| tại hai điểm phân biệt

⇔ m < 11/2 (tung độ điểm A).

Vậy với m < 11/2 thì phương trình |x – 4| - |2x + 3| - m = 0 có hai nghiệm phân biệt.

Bài 9: Bằng đồ thị, biện luận số nghiệm của phương trình |x| + |x-2| = m.

Hướng dẫn giải:

Xét hàm số y = |x| + |x – 2|

+ Xét x ≤ 0, hàm số trở thành y = -x + (2 – x) = 2 – 2x

+ Xét 0 < x < 2, hàm số trở thành y = x + (2 – x) = 2.

+ Xét x ≥ 2, hàm số trở thành y = x + x – 2 = 2x – 2.

Suy ra

Đồ thị hàm số trên gồm ba phần:

+ Phần đường thẳng y = 2 – 2x lấy các điểm có hoành độ nhỏ hơn hoặc bằng 0.

+ Phần đường thẳng y = 2 lấy các điểm có hoành độ từ 0 đến 2.

+ Phần đường thẳng y = 2x – 2, lấy các điểm có hoành độ lớn hơn hoặc bằng 2.

Ta có đồ thị như hình vẽ dưới (đường đồ thị màu đỏ):

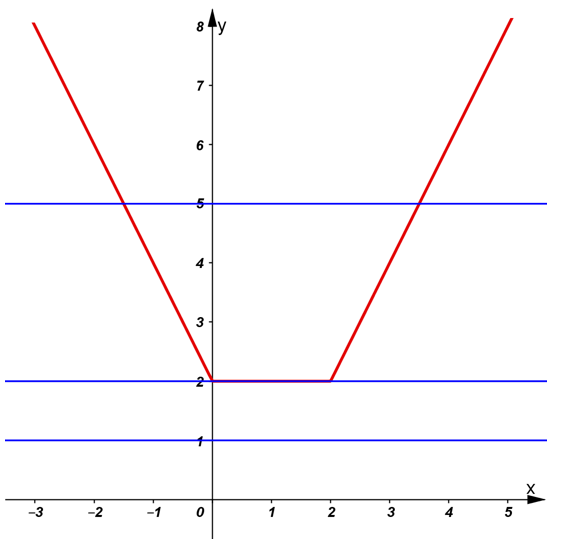
Số nghiệm phương trình phụ thuộc số giao điểm của đường thẳng y = m và đồ thị hàm số y = |x| + |x – 2|.

+ Nếu m < 2, số giao điểm là 0, phương trình vô nghiệm.

+ Nếu m = 2, số giao điểm là vô số, phương trình có vô số nghiệm.

+ Nếu m > 2, số giao điểm bằng 2, phương trình có hai nghiệm.

Kết luận: Với m < 2, phương trình vô nghiệm.

Với m = 2, phương trình có vô số nghiệm.

Với m > 2, phương trình có hai nghiệm.

Bài 10: Cho hàm số

a) Vẽ đồ thị hàm số trên.

b) Tìm giá trị nhỏ nhất của hàm số.

c) Biện luận theo m số nghiệm của phương trình: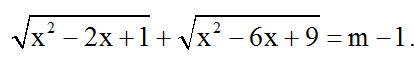

Hướng dẫn giải:

a) Ta có:

+ Xét x ≤ 1, y = (1 – x) + (3 – x) = 4 – 2x.

+ Xét 1 < x < 3, y = x – 1 + 3 – x = 2.

+ Xét x ≥ 3, y = x – 1 + x – 3 = 2x – 4.

⇒

Đồ thị hàm số gồm ba phần :

+ Phần đường thẳng y = 4 – 2x lấy các điểm có hoành độ nhỏ hơn hoặc bằng 1.

+ Phần đường thẳng y = 2 lấy các điểm có hoành độ từ 1 đến 3.

+ Phần đường thẳng y = 2x – 4 lấy các điểm có hoành độ lớn hơn hoặc bằng 3.

Ta có đồ thị hàm số như hình vẽ dưới :

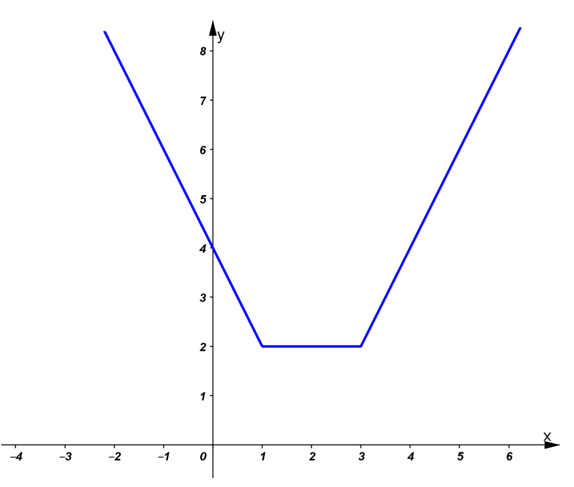
b) Quan sát đồ thị hàm số, nhận thấy điểm thuộc đồ thị hàm số có tung độ nhỏ nhất bằng 2.

Vậy hàm số đạt giá trị nhỏ nhất bằng 2 tại mọi x thỏa mãn 1 ≤ x ≤ 3.

c) Số nghiệm của phương trình 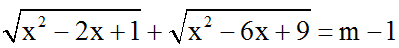là số giao điểm của đường thẳng y = m – 1 và đồ thị hàm số

+ Nếu m – 1 < 2 hay m < 3 ⇒ hai đồ thị không có giao điểm ⇒ phương trình vô nghiệm.

+ Nếu m – 1 = 2 hay m = 3 ⇒ có vô số giao điểm ⇒ phương trình có vô số nghiệm.

+ Nếu m – 1 > 2 hay m > 3 ⇒ có hai giao điểm ⇒ phương trình có hai nghiệm.

Kết luận: Với m < 3, phương trình vô nghiệm.

Với m = 3, phương trình có vô số nghiệm.

Với m > 3, phương trình có hai nghiệm.