Công thức nghiệm của phương trình ax+by=c - Toán lớp 9
Công thức nghiệm của phương trình ax+by=c
Với Công thức nghiệm của phương trình ax+by=c Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Công thức nghiệm của phương trình ax+by=c từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải
Tập nghiệm của phương trình bậc nhất hai ẩn
Phương trình bậc nhất hai ẩn ax + by = c luôn có vô số nghiệm.
Tập nghiệm của phương trình được biểu diễn bởi đường thẳng (d) ax + by = c.

B. Bài tập tự luận
Bài 1: Cho phương trình 3x - 2y = 1
a) Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm trên mặt phẳng tọa độ.
b) Tìm nghiệm của phương trình.
Hướng dẫn giải


Bài 2: Xác định phương trình bậc nhất hai ẩn có các nghiệm là (1;-3) và (-2;0). Viết công thức nghiệm tổng quát của phương trình đó.
Hướng dẫn giải
Xét phương trình bậc nhất hai ẩn có dạng tổng quát ax + by = c (a ≠ 0 hoặc b ≠ 0)
+ Thay x = 1; y = -3 và phương trình ta có: a – 3b = c (1)
+ Thay x = -2; y = 0 vào phương trình ta có: -2a = c (2)
Thay (2) vào (1) ta được a - 3b = -2a ⇔ 3a = 3b ⇔ a = b.
Khi đó phương trình có dạng ax + ay = -2a ⇔ x + y = -2 (do a ≠ 0).
Công thức nghiệm tổng quát của phương trình là x ∈ R và y= -x - 2 hoặc x= -y - 2 và y ∈ R
Bài 3: Viết công thức nghiệm của các phương trình sau và biểu diễn tập nghiệm trên mặt phẳng tọa độ.
a) 3x - y = 1/2
b) x + 5y = 0
Hướng dẫn giải
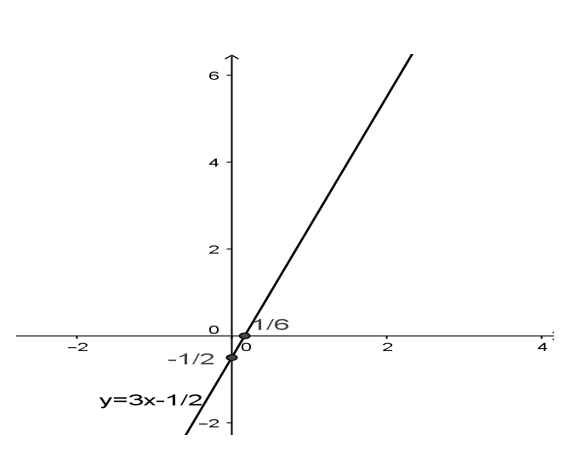
a) 3x - y = 1/2
Công thức nghiệm tổng quát của phương trình là:
x ∈ R; y = 3x - 1/2
Biểu diễn hình học:
| x | 0 | 1/6 |
| y | -1/2 | 0 |
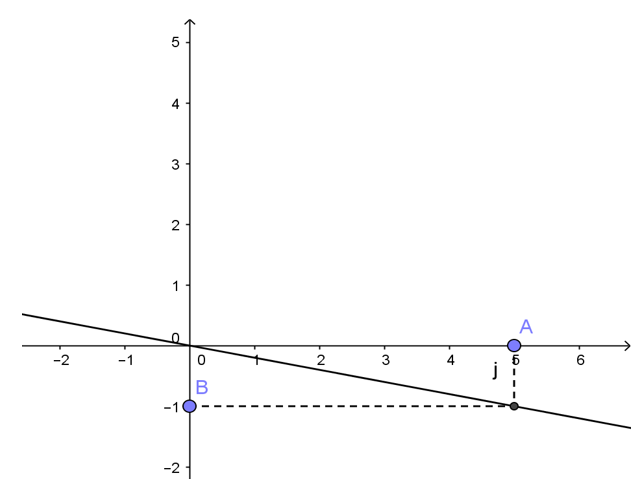
b) x + 5y = 0
Công thức nghiệm tổng quát của phương trình là:
x ∈ R; y = -x/5
Biểu diễn hình học
| x | 0 | 5 |
| y | 0 | -1 |
Bài 4: Tìm nghiệm nguyên của các phương trình sau:
a) x + 3y = 1
b) 4x - 5y = 24
Hướng dẫn giải



