Bài tập trắc nghiệm Giải phương trình, bất phương trình vô tỷ - Toán lớp 9

Bài tập trắc nghiệm Giải phương trình, bất phương trình vô tỷ

Với Bài tập trắc nghiệm Giải phương trình, bất phương trình vô tỷ Toán lớp 9 tổng hợp 10 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Giải phương trình, bất phương trình vô tỷ từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Phương trình 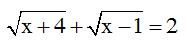có tập nghiệm là:

A. S= {1;-4}

B. S= {1}

C. S= ∅

D. S= {-4}

Câu 2: Câu nào sau đây đúng:

Câu 3: Nghiệm của phương trình 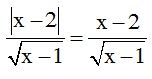thỏa mãn điều kiện nào sau đây:

A. x > 1

B. x ≥ 2

C. x < 2

D. Một điều kiện khác.

Câu 4:Phương trình 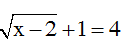có nghiệm x bằng:

A. 5    B. 11    C. 121    D. 25

Câu 5: Phương trình 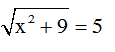có nghiệm x bằng

A. 4    B. -4    C.±4    D. 5

Câu 6: Nghiệm của bất phương trình 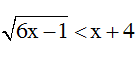là:

A. x > 1/6    B. x < 1/6    C. x ≥ 1/6    D. x ≤ 1/6

Hướng dẫn giải và đáp án

Câu 1: Thay x=1 vào phương trình, ta thấy không thỏa mãn. Suy ra x=1 không là nghiệm

Thay x=-4 vào phương trình, ta thấy không thỏa mãn. Suy ra x=-4 cũng không là nghiệm của phương trình.Vậy phương trình đã cho vô nghiệm

Vậy chọn đáp án: C

Câu 2: Chọn đáp án: D

Câu 3: Điều kiện: x - 1 > 0 ⇔ x > 1

Ta có:

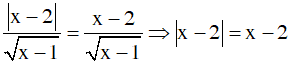
=> x - 2 ≥ 0 ⇔ x ≥ 2

Kết hợp với điều kiện ta được: x ≥ 2

Vậy chọn đáp án: B

Câu 4: Thử tất cả các đáp án, ta thấy khi thay x=11 vào phương trình ta được:

√(11-2) + 1 = 4 ( luôn đúng)

Vậy x=11 là nghiệm của phương trình.

Vậy chọn đáp án: B

Câu 5:Điều kiện: x² + 9 ≥ 0 (luôn đúng vì x² ≥ 0 )

Khi đó: x² + 9 = 25 ⇔ x² = 16 ⇔ x = ±4

Vậy x = ±4 .

Vậy chọn đáp án: C

Câu 6: Điều kiện:

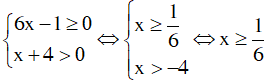
Khi đó:

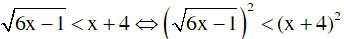
⇔ 6x - 1 < x² + 8x + 16

⇔ x² + 2x + 17 > 0

⇔ (x+1)² + 16 > 0 (luôn đúng)

Vậy chọn đáp án C