Chuyên đề Đường tròn - Toán lớp 9

---

Chuyên đề Đường tròn

Với Chuyên đề Đường tròn Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

• Đường tròn
• Liên hệ giữa dây và khoảng cách từ tâm đến dây
• Vị trí tương đối của đường thẳng với đường tròn. Tiếp tuyến của đường tròn
• Tính chất của hai tiếp tuyến cắt nhau
• Vị trí tương đối của 2 đường tròn
• Ôn tập chương 2

Đường tròn

A. Phương pháp giải

1, Định nghĩa đường tròn

Đường tròn là quỹ tích những điểm cách đều một điểm cố định trong mặt phẳng.

Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.

Chú ý:

- Không vẽ được đường tròn nào đi qua ba điểm thẳng hàng.

- Nếu hai đường tròn có 3 điểm chung thì chúng phải trùng nhau

- Để xác định một đường tròn ta xác định tâm và bán kính của nó hoặc 3 điểm phân biệt thuộc đường tròn.

- Để chứng minh nhiều điểm nằm trên một đường tròn ta chứng minh điểm ấy cách đều 1 điểm xác định.

2. Định lý

a, Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

b, Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

3. Tính chất đối xứng

-Tâm của đường tròn là tâm đối xứng của đường tròn đó.

- Bất kỳ đường kính nào của đường tròn cũng là trục đối xứng của đường tròn đó.

4. Các định lý liên quan đến dây cung và đường kính

1, Trong các dây cung của một đường tròn, dây cung lớn nhất là đường kính.

2, Trong một đường tròn, đường kính vuông góc với một dây cung thì đi qua trung điểm dây ấy. Ngược lại, đường kính đi qua trung điểm của một dây cung( không phải là đường kính) thì vuông góc với dây cung ấy.

B. Bài tập tự luận

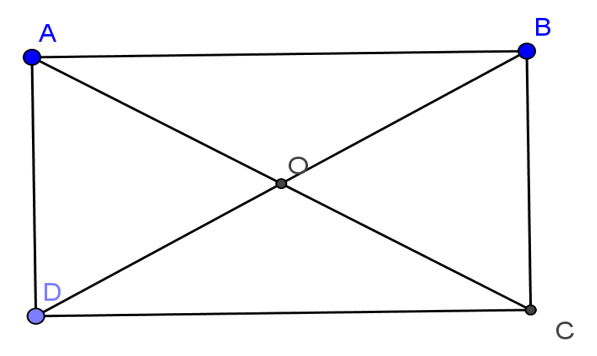
Bài 1: Cho hình chữ nhật ABCD có AD=12cm, CD=16cm. Chứng minh rằng 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Hướng dẫn giải

Gọi O là giao điểm của hai đường chéo AC và BD.

Ta có OA = OB = OC = OD nên bốn điểm A, B,C,D thuộc cùng một đường tròn( tâm O, bán kính OA).

AC² = AD² + DC² = 12² + 16² = 400

=> AC = 20

Bán kính của đường tròn bằng 10cm.

Bài 2: Trong các câu sau, câu nào đúng? Câu nào sai?

a, Hai đường tròn phân biệt có thể có hai điểm chung.

b, Hai đường tròn phân biệt có thể có ba điểm chung phân biệt

c, Tâm của đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác ấy.

Hướng dẫn giải

a. Đúng

b. Sai

c. Đúng

Bài 3: Cho tam giác ABC cân tại A, nội tiếp đường tròn(O). Đường cao AH cắt đường tròn ở D.

a, Vì sao AD là đường kính của đường tròn (O).

b, Tính số đo góc ACD

c, Cho BC=24cm,AC=20cm. Tính đường cao AH và bán kính đường tròn (O)

Hướng dẫn giải

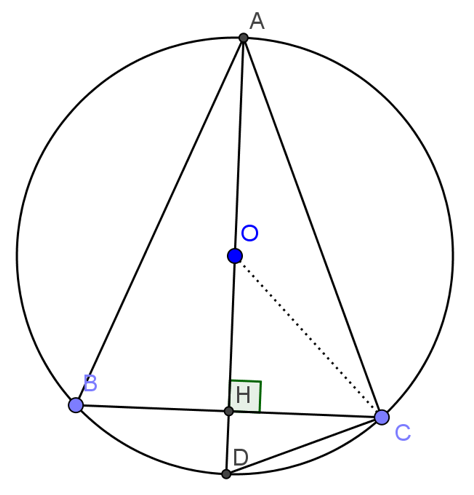
a, Tam giác ABC cân tại A nên AH là đường trung trực của BC. Do đó AD là đường trung trực của BC. Vì O nằm trên đường trung trực của BC nên O nằm trên AD. Vậy AD là đường kính của đường tròn (O).

b, Tam giác ACD nội tiếp đường tròn đường kính AD nên ∠ACD = 90^o

c, Ta có BH = HC = BC/2 = 12(cm)

Tam giác AHC vuông tại H nên AH² = AC² - HC² = 20² - 12² = 256

=> AH = 16(cm)

AC² = AD. AH

AD = AC²/AH = 25(cm)

Bán kính đường tròn(O) bằng 12,5cm.

Bài 4: Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng:

a, Bốn điểm B, C, H, K cùng thuộc một đường thẳng.

b, HK < BC

Hướng dẫn giải

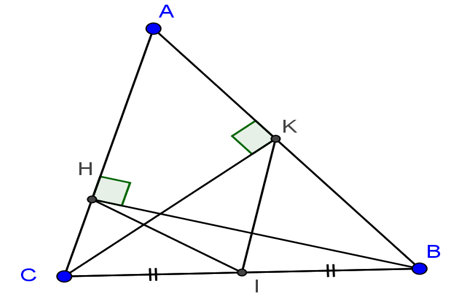
Gọi I là trung điểm của BC.

Áp dụng định lý” Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.”

Xét tam giác vuông CBH có HI là trung tuyến ứng với cạnh huyền BC => HI = 1/2 BC (1)

Xét tam giác vuông CBK có KI là trung tuyến ứng với cạnh huyền BC => KI = 1/2 BC (2)

Từ (1) và (2) ta suy ra HI=KI=IB=IC. Vậy bốn điểm B, K, H, C cùng thuộc đường tròn tâm I bán kính IB.

b, Trong đường tròn tâm (I) ở trên, HK là dây, BC là đường kính nên KH < BC.(Dây cung bao giờ cũng nhỏ hơn đường kính).

Liên hệ giữa dây và khoảng cách từ tâm đến dây

A. Phương pháp giải

Định lý: Trong một đường tròn:

- Hai dây cung bằng nhau thì cách đều tâm,

- Hai dây cung cách đều tâm thì bằng nhau.

- Dây cung nào lớn hơn thì gần tâm hơn.

- Dây cung gần tâm hơn thì lớn hơn.

B. Bài tập tự luận

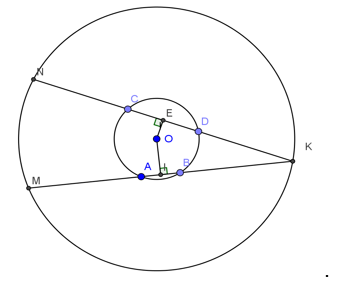
Bài 1: Cho hình vẽ sau, trong đó MN=PQ. Chứng minh rằng:

a, AE=AF

b, AN=AQ.

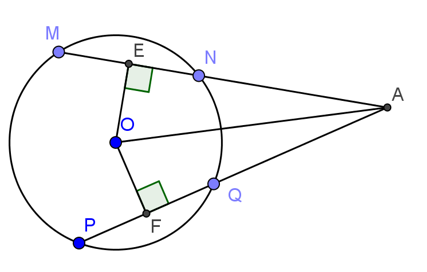
Hướng dẫn giải

Vì MN=PQ nên OE=OF( theo định lý liên hệ giữa dây và khoảng cách từ tâm đến dây)

Xét tam giác vuông AOE và tam giác vuông AOF có:

OE=OF ( chứng minh trên)

AO: chung

Suy ra ΔAOE = ΔAOF ( cạnh huyền-cạnh góc vuông)

Suy ra AE=AF( 2 cạnh tương ứng)(1)

Vì OE⊥MN nên ME=NE (tính chất đường kính và dây cung)

Vì OF⊥PQ nên PF=QF (tính chất đường kính và dây cung)

Mà MN=PQ

Suy ra ME=NE=PF=QF.(2)

Từ (1) và (2) suy ra AN=AQ.

Bài 2: Cho đường tròn(O), dây AB và dây CD, AB < CD. Giao điểm K của các đường thẳng AB, CD nằm ngoài đường tròn. Đường tròn (O;OK) cắt KA và KC tại M và N.

Chứng minh KM < KN.

Hướng dẫn giải

Kẻ OI ⊥AB, OE ⊥ CD.

Xét đường tròn (O;OA) có: AB và CD là dây cung, AB < CD. Suy ra OI > OE.

Xét đường tròn (O;OK) có KN và KM là dây cung và OI > OE. Suy ra KM < KN.

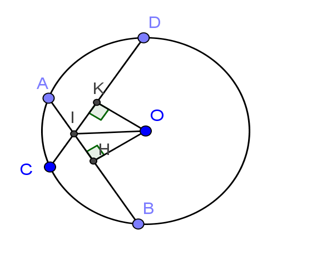
Bài 3: Cho đường tròn (O), hai dây AB, CD bằng nhau và cắt nhau tại điểm I nằm bên trong đường tròn. Chứng minh rằng:

a, IO là tia phân giác của một trong hai góc tạo bởi hai dây AB và CD.

b, Điểm I chia AB, CD thành các đoạn thẳng bằng nhau đôi một.

Hướng dẫn giải

a, Kẻ OH ⊥ AB; OK ⊥ CD.

Vì CD=AB nên OK=OH.

Xét tam giác vuông IKO và tam giac vuông IOH ta có:

OK=OH

IO: chung

Suy ra Δ IKO = ΔIOH ( cạnh huyền-cạnh góc vuông)

=> ∠KIO = ∠OIH ( 2 góc tương ứng)

Suy ra OI là tia phân giác của góc BID

b, Theo câu a, Δ IKO = ΔIOH ( cạnh huyền-cạnh góc vuông)

=> IH=IK.

Xét đường tròn tâm (O), ta có: OK ⊥ CD nên suy ra CK=KD( định lý về đường kính và dây) (1)

Xét đường tròn tâm (O), ta có: OH ⊥ AB nên suy ra AH=HB (định lý về đường kính và dây) (2)

Từ (1) và (2) ta có: CK=AH

Mặt khác, IH=IK

Suy ra AI=CI

Vì CD=AB, mà AI=CI(chứng minh trên) nên ta suy ra ID=IB.

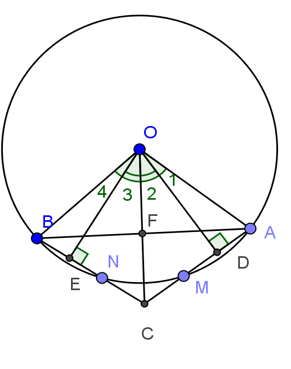
Bài 4: Cho đường tròn (O), các bán kính OA và OB. Trên cung nhỏ AB lấy các điểm M và N sao cho AM=BN. Gọi C là giao điểm của các đường thẳng AM và BN. Chứng minh rằng:

a, OC là tia phân giác của góc AOB.

b, OC vuông góc AB.

Hướng dẫn giải

Xét đường tròn tâm (O) có AM=BN

Từ đó ta suy ra OE=OD (tính chất quan hệ giữa đường kính và dây cung)

Xét tam giác vuông AOD và tam giác vuông BOE có:

OA=OB(cùng bằng bán kính)

OE=OD(chứng minh trên)

=> ΔAOD = ΔBOE (cạnh huyền-cạnh góc vuông)

=> ∠O₁ = ∠O₄ (2 góc tương ứng)(1)

Tương tự ta có: ∠O₂ = ∠O₃ (2)

Ta có: ∠AOC = ∠O₁ + ∠O₂

∠BOC = ∠O₃ + ∠O₄

Từ (1) và (2) ta suy ra ∠AOC= ∠BOC

Suy ra OC là tia phân giác của góc AOB.

Xét tam giác OBF và tam giác OAF có:

∠AOC = ∠BOC (chứng minh trên)

OA=OB

OF: chung

Suy ra ΔOBF = ΔOAF (c-g-c)

=> BF=AF( 2 cạnh tương ứng)

=> OC ⊥ AB

Vị trí tương đối của đường thẳng với đường tròn. Tiếp tuyến của đường tròn

A. Phương pháp giải

Vị trí tương đối của đường thẳng với đường tròn.

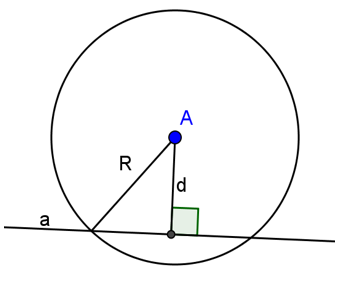
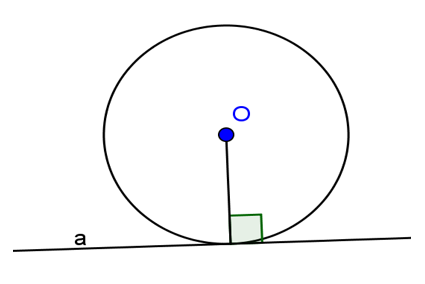
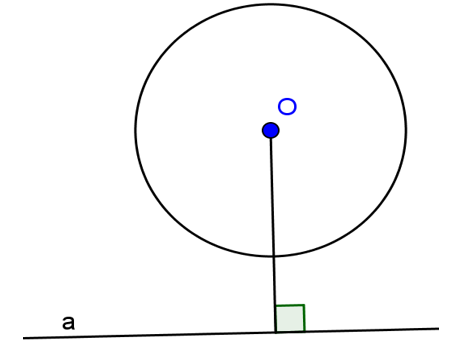
Gọi d là khoảng cách từ tâm O của đường tròn (O; R) đến đường thẳng a.

+ d < R: a cắt tại (O; R) tại 2 điểm

+ d = R: a cắt (O; R) tại 1 điểm. Trường hợp này a tiếp xúc với đường tròn hay a là tiếp tuyến của đường tròn.

+ d > R: a không căt đường tròn.

2, Tiếp tuyến với đường tròn tại 1 điểm thuộc đường tròn

a, Định nghĩa:

Một đuờng thẳng được gọi là tiếp tuyến với đường tròn nếu nó chỉ có một điểm chung với đường tròn.

b, Định lý:

- Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

- Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng đó là tiếp tuyến của đường tròn đó.

Chú ý: Để chứng minh một đường thẳng là tiếp tuyến của một đường tròn tại một điểm thuộc đương tròn, ta chứng minh đường thẳng vuông góc với bán kính qua điểm ấy của đường tròn.

B. Bài tập tự luận

Bài 1: Trong hệ tọa độ Oxy cho điểm A(4;3). Hãy xác định vị trí tương đối của đường tròn tâm A, bán kính R=3 với các trục tọa độ.

Hướng dẫn giải

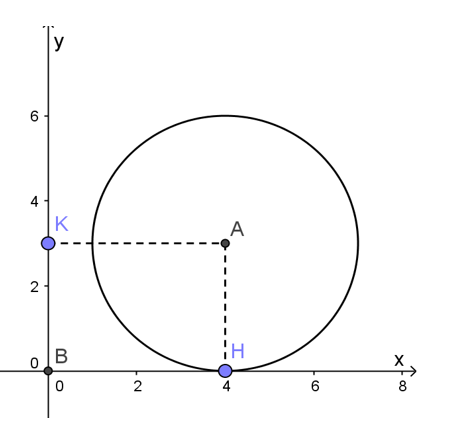
Khoảng cách từ A đến trục Ox là: d = AH = OK = 3.

Khoảng cách từ A đến trục Oy là d’ = AK = OH = 4.

Do đó đường tròn (A;3) tiếp xúc với trục Ox, vì d = R = 3; đường tròn (A;3) không cắt trục Oy vì d’= 4 > 3 = R.

Bài 2: Cho điểm A nằm trong đường tròn (O). Chứng minh rằng mọi đường thẳng d đi qua A đều cắt (O) ở hai điểm phân biệt.

Hướng dẫn giải

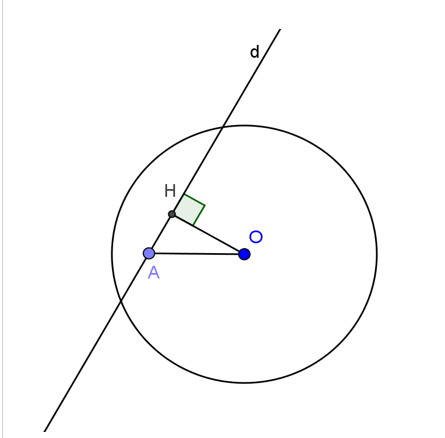
Vẽ OH ⊥ d tại H => OH ≤ OA (quan hệ đường xiên và đường vuông góc).

Vì A nằm trong (O) nên OA < R.

Suy ra OH < R đường thẳng d luôn cắt (O) tại 2 điểm phân biệt.

Bài 3: Từ điểm A cách O một khoảng d (d > R) vẽ tiếp tuyến AB với đường tròn (O;R) (B: là tiếp điểm). Tính độ dài đoạn AB.

Hướng dẫn giải

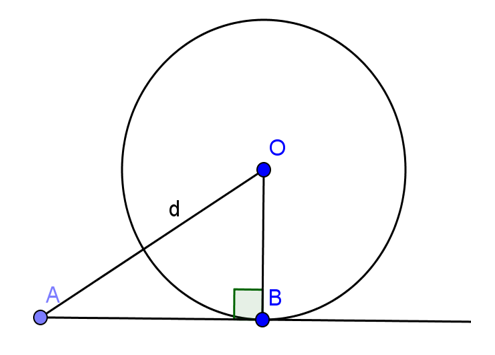Vì AB là tiếp tuyến của (O) tại B nên AB ⊥ OB tại B Áp dụng định lý Py-ta-go vào ΔAOB có:

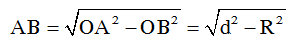
Bài 4: Cho đường tròn (O;5 cm) và dây AB=8cm. Một tiếp tuyến của (O) song song với AB cắt tia OA tại E, cắt tia OB tại F. Tính độ dài EF.

Hướng dẫn giải

Gọi C là tiếp điểm của tiếp tuyến EF với (O), H là giao điểm của OC với AB.

Ta có: OC ⊥ EF tại C mà AB//EF nên OC ⊥ AB tại H.

=> HA = HB = 1/2AB = 4(cm)

Áp dụng định lý Pi-ta-go vào tam giác OHA có:

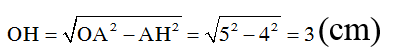
Ta có: AB//EF nên theo định lý Ta –lét ta có:

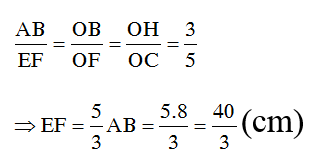
Vậy EF=40/3(cm)