Chuyên đề Phương trình bậc hai một ẩn số - Toán lớp 9

---

Chuyên đề Phương trình bậc hai một ẩn số

Với Chuyên đề Phương trình bậc hai một ẩn số Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình bậc hai một ẩn số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

• Hàm số y= ax² (a ≠ 0)
• Bài tập trắc nghiệm Hàm số y= ax² (a ≠ 0)
• Đồ thị hàm số y= ax²
• Giải và biện luận phương trình bậc hai
• Bài tập trắc nghiệm Giải phương trình bậc hai
• Hệ thức Vi-et và ứng dụng
• Bài tập trắc nghiệm Áp dụng định lí Vi-ét
• Phương trình quy về phương trình bậc hai
• Giải bài toán bằng cách lập phương trình
• Ôn tập chương 4

Hàm số y= ax^2 (a ≠ 0)

A. Phương pháp giải

Tính chất của hàm số y= ax²

- Nếu a > 0 thì hàm số y= ax² nghịch biến khi x < 0, đồng biến khi x > 0;

y > 0 với mọi x ≠ 0

y = 0 khi x = 0, y = 0 là giá trị nhỏ nhất của hàm số

- Nếu a < 0 : hàm số y= ax² nghịch biến khi x > 0, đồng biến khi x < 0;

y < 0 với mọi x ≠ 0

y = 0 khi x = 0, y = 0 là giá trị lớn nhất của hàm số

B. Bài tập tự luận

Bài 1: Cho hàm số y= (m² + 2m + 2)x²

a) Chứng tỏ rằng hàm số nghịch biến với mọi x < 0, đồng biến với mọi x > 0.

b) Biết rằng khi x= ±2 thì y = 8. Tìm m.

Hướng dẫn giải

a) Hàm số đã cho có dạng y=ax² trong đó a= m² + 2m + 2 =(m + 1)² + 1 > 0 với mọi m. Do đó:

+ Hàm số đã cho nghịch biến với mọi x < 0.

+ Hàm số đã cho đồng biến với mọi x > 0.

b) Thay x= ±2 thì y = 8

(m² + 2m + 2)(±2)² = 8 ⇔ (m² + 2m + 2).4 = 8

⇔ (m² + 2m + 2)= 2 ⇔ m² + 2m = 0 => m = 0 hoặc m = -2.

Vậy m = 0 hoặc m = -2.

Bài 2: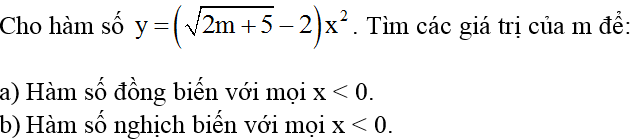

Hướng dẫn giải

Bài 3: : Chọn đáp án đúng.

Tại x = 4 hàm số y= -1/2 x² có giá trị bằng:

A. 8 B. -8 C. -4 D. 4

Hướng dẫn giải

Đáp án đúng B

Bài tập trắc nghiệm Hàm số y= ax^2 (a ≠ 0)

Câu 1: Chọn đáp án đúng.

Tại x = 4 hàm số y= -1/2 x² có giá trị bằng:

A. 8    B. -8    C. -4    D. 4

Câu 2: Hàm số y= (m - 1/2)x² đồng biến khi x > 0 nếu:

A. m < 1/2    B. m > 1/2    C. m > -1/2    D. m = 0

Câu 3: Hàm số y= -x² nghịch biến khi:

A. x ≠ R

B. x > 0

C. x = 0

D. x < 0

Câu 4: Cho hàm số y= ax² ( a ∈ 0) có đồ thị là parabol (P). Tìm a biết điểm A(-4; -1) thuộc P?

A. a = -16

B. a = 1/16

C. a = -1/16

D. Kết quả khác.

Câu 5: Đồ thị hàm số y= 2x và y= -x²/2 cắt nhau tại các điểm

A. (0; 0)

B. (-4; -8)

C. (0; -4)

D. (0; 0) và (-4; -8)

Câu 6: Đồ thị hàm số y=ax² đi qua điểm A(1; 1). Khi đó hệ số a bằng:

A. -1    B. 1   C. ±1    D. 0

Câu 7: Đường thẳng (d): y=-x+6 và Parabol (P): y = x²

A. Tiếp xúc nhau

B. Cắt nhau tại 2 điểm A(-3; 9) và B(2;4)

C. Không cắt nhau

D. Kết quả khác

Câu 8: Tọa độ giao điểm của đường thẳng (d): y=x-2 và Parabol (P): y= -x² là:

A. (1;1) và (-2;4)

B. (1; -1) và (-2; -4)

C. (-1; -1) và (2; -4)

D. (1;-1)

Câu 9: Đồ thị hàm số y = 2x và y= -x²/2 cắt nhau tại các điểm:

A (0; 0)

B (-4; -8)

C (0;-4)

D (0; 0) và (-4; -8)

Câu 10: Điểm M(-2; 1) thuộc đồ thị hàm số nào:

A. y= 1/5 x²

B. y= x²

C. y= 5x²

D. y=2x+5

Câu 11: Biết hàm số y=ax² (a ∈ 0) đi qua điểm có tọa độ (1; -2) , khi đó hệ số a bằng:

A. a=-2    B. a=2    C. a=-3    D. a=5

Câu 12: Điểm M(-1; -2) thuộc đồ thị hàm số y= mx² khi giá trị của m bằng:

A.-4    B.-2    C. 2    D.4

Câu 13: Đường thẳng nào không cắt Parabol(P) y= x²

A. y=2x+5

B. y=-3x-6

C. y=-3x+5

D. y=-3x-1

Câu 14: Giữa (P): y= -x²/2 và đường thẳng (d): y=x+1 có các vị trí tương đối sau:

A.(d) tiếp xúc (P)

B.(d) cắt (P)

C.(d) vuông góc với (P)

D. Không cắt nhau

Hướng dẫn giải và đáp án

Câu 1: Thay x = 4 vào hàm số y= -1/2 x² ta được: y=-4² / 2 = -8

Vậy chọn đáp án: B

Câu 2: Hàm số y= ax² đồng biến khi a > 0. Vì vậy, hàm số y = (m -1/2)x² đồng biến khi (m-1/2) > 0. Suy ra m > 1/2.

Vậy chọn đáp án: B

Câu 3: Đáp án: A

Câu 4: Thay x=-4; y=-1 vào hàm số y= ax² ta được: -1=a.(-4)². Từ đó, ta suy ra a = -1/16

Vậy chọn đáp án: C

Câu 5: Giải phương trình hoành độ: 2x = -x²/2

Suy ra x= 0 hoặc x= -4

Với x= 0 ta được y= 0. Suy ra A(0; 0)

Với x= -4 ta được y= -8. Suy ra B(-4; -8)

Câu 6: Chọn đáp án:B

Câu 7: Giải phương trình hoành độ: -x+6=x².Suy ra x= 2 hoặc x= -3

Với x= 2, ta được y= 4

Với x= -3, ta được y= 9

Vậy chọn đáp án B

Câu 8: Chọn đáp án: B

Câu 9: Chọn đáp án: D

Câu 10: Chọn đáp án: D

Câu 11: Chọn đáp án A

Câu 12: Thay x= -1; y= -2 vào đồ thị hàm số ta được: -2 = m.

Vậy chọn đáp án: B

Câu 13: Chọn đáp án: B

Câu 14: Xét phương trình hoành độ: -x²/2 = x + 1

⇔ x² + 2x + 2 = 0. Phương trình này có Δ' = -1 < 0 nên phương trình đã cho vô nghiệm

Vậy chọn đáp án D

Đồ thị hàm số y= ax^2

A. Phương pháp giải

Đồ thị hàm số y= ax² (a ≠ 0) là một parabol đi qua gốc tọa đọ O, nhận trục tọa độ Oy làm trục đối xứng; O là đỉnh của parabol

- Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị.

- Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị.

B. Bài tập tự luận

Bài 1: Chọn đáp án đúng

Điểm P(-1; -2) thuộc đồ thị hàm số y= -mx² khi m bằng:

A. -2    B. 2    C. -4    D. 4

Hướng dẫn giải

Đáp án B

Bài 2: Điểm thuộc đồ thị hàm số y= -1/3x² là:

A. M(1;1/3)    B. N(1/3;1)    C. P(1;-1/3)    D. Q(-1/3;1)

Hướng dẫn giải

Đáp án C

Bài 3: Điểm thuộc đồ thị hàm số y= -1/3x² là:

A. M(2;-4/3)    B. N(-2; -4/3)    C. P(1;1/3)    D. Q(1;-1/3)

Hướng dẫn giải

Đáp án C

Bài 4: a) Xác định hệ số của hàm số y=ax² biết rằng đồ thị của nó đi qua điểm A(1; -1). Vẽ đồ thị của hàm số với a vừa tìm được.

b) Tìm điểm thuộc parabol nói trên có hoành độ bằng 3.

c) Tìm diểm thuộc parabol có tung độ bằng 3.

d) Tìm điểm thuộc parabol có tung độ gấp đôi hoành độ.

Hướng dẫn giải