Bài tập trắc nghiệm Góc với đường tròn - Toán lớp 9

---

Bài tập trắc nghiệm Góc với đường tròn

Với Bài tập trắc nghiệm Góc với đường tròn Toán lớp 9 tổng hợp 31 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Góc với đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Tâm đường tròn ngoại tiếp tam giác là:

A. Giao điểm 3 đường phân giác của tam giác

B. Giao điểm 3 đường cao của tam giác

C. Giao điểm 3 đường trung tuyến của tam giác

D. Giao điểm 3 đường trung trực của tam giác

Câu 2: Đường tròn tâm A có bán kính 3cm là tập hợp các điểm:

A. Có khoảng cách đến điểm A nhỏ hơn hoặc bằng 3cm

B. Có khoảng cách đến A bằng 3cm

C. Cách đều A

D. Có hai câu đúng

Câu 3: Cho tam giác ABC nội tiếp đường tròn tâm O. Biết ∠A = 50^o , ∠B = 65^o. Kẻ OH ⊥ AB; OI ⊥ AC; OK ⊥ BC. So sánh OH, OI, OK ta có:

A. OH = OI = OK

B. OH = OI > OK

C. OH = OI < OK

D. Một kết quả khác

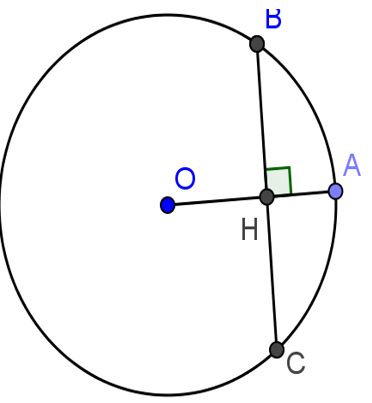
Câu 4: Trong hình bên, biết BC=8cm, OB=5cm.Độ dài AB bằng:

A. 20cm

B. √6cm

C. 2√5cm

D. Một kết quả khác

Câu 5: Cho đường tròn(O; R) và dây AB = R√3, Ax là tia tiếp tuyến tại A của đường tròn (O). Số đo của ∠xAB là:

A. 90^o

B. 120^o

C. 60^o

D. B và C đúng

Câu 6: Cho đường tròn (O; R) và điểm A bên ngoài đường tròn. Từ A xẽ tiếp tuyến AB( B là tiếp điểm) và cát tuyến AMN đến (O). Trong các kết luận sau , kết luận nào đúng?

A. AM.AN = 2R²

B. AB²= AM.MN

C. AO²= AM.AN

D. AM.AN = AO² - R²

Câu 7: Cho tứ giác ABCD nội tiếp đường tròn(O). Biết ∠BOD = 124^o thì số đo ∠BAD là:

A. 56^o

B. 118^o

C. 124^o

D. 62^o

Hướng dẫn giải và đáp án

Câu 1: Chọn D

Câu 2: Chọn đáp án: B

Câu 3: Xét tam giác ABC ta tính được ∠C = 180^o - 50^o - 65^o = 65^o (vì tổng 3 góc trong một tam giác bằng 180)

Từ đó suy ra AB= AC > BC(trong một tam giác, góc đối diện với cạnh lớn hơn thì lớn hơn)

Suy ra OH = OI < OK.

Chọn đáp án: C

Câu 4: Ta có: OA ⊥ BC nên ta suy ra BH = HC = 8 : 2 = 4cm( vì đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy)

Xét tam giác vuông OBH có: OH²= OB² - HB² = 25 - 16 = 9cm

Suy ra OH=3cm. Suy ra HA=5-3=2cm.

Xét tam giác vuông HAB có: AB²= HA² + HB²

Thay số ta được: AB² = 4 + 16 = 20cm

=>AB = √20cm = 2√5cm

Vậy chọn đáp án:C

Câu 5: Xét tam giác AOB . Theo đinh lý cosin ta có:

AB² = AO² + OB² - 2OA.OB.cos ∠AOB

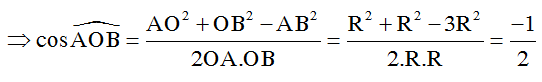
=> ∠AOB = 120^o

=> ∠xAB = 60^o (vì góc tạo bởi tia tiếp tuyên và dây cung bằng một nửa góc ở tâm)

Vậy chọn đáp án: C

Câu 6: Ta có: ∠ABM = 1/2 sdBM (góc tạo bởi tia tiếp tuyến và dây cung)

∠MNB = 1/2 sdBM( góc nội tiếp chắn cung BM)

=> ∠ABM = ∠MNB

Xét tam giác ABM và tam giác ANB có:

∠A :chung

∠ABM = ∠MNB

Suy ra ΔABM ∼ ΔANB (g-g)

=> AB/AN = AM/AB => AB² = AN.AM

Chọn B

Câu 7: Ta có: ∠BOD = 124^o => sdBD = 62^o => ∠BAD = 62^o (góc nội tiếp chắn nửa đường tròn bằng một nửa số đo của cung đó)

Vậy chọn đáp án: D

Câu 8: Cho 2 đường tròn (O;4cm) và (O; 3cm) có O O’=5cm. Hai đường tròn trên cắt nhau tại A và B. Độ dài AB bằng:

A. 2,4 cm B. 4,8cm C. 5/12 cm D. 5cm

Câu 9: Cho đường tròn (O; 2cm). Từ điểm A sao cho OA=4cm. Vẽ tiếp tuyến AB, AC đến đường tròn (O) (B, C là tiếp điểm). Chu vi tam giác ABC là:

A. 6√3

B. 5√3

C. 4√3

D. 2√3

Câu 10: Cho đường tròn (O) và góc nội tiếp ∠BAD = 130^o. Số đo của góc ∠BOD là:

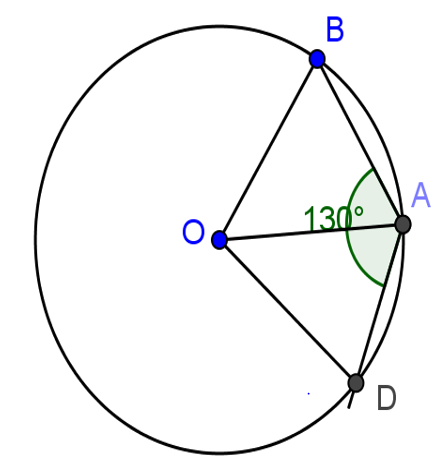
A. 130^o

B. 100^o

C. 260^o

D. 50^o

Câu 11: Cho đường tròn (O; R). Nếu bán kính R tăng 1,2 lần thì diện tích hình tròn (O; R) tăng mấy lần:

A. 1,2

B. 2,4

C. 1,44

D. Một kết quả khác

Câu 12: Cho tam giác ABC vuông cân tại A và AC=8. Bán kính đường tròn ngoại tiếp tam giác ABC là:

A. 4 B. 8√2 C. 16 D. 4√2

Câu 13: Trong các mệnh đề sau, mệnh đề nào đúng:

A. Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

B. Nếu một đường thẳng vuông góc với bán kính của một đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.

C. Trong hai dây cung của một đường tròn, dây nhỏ hơn thì gần tâm hơn.

D. A, B, C đều đúng

Câu 14: Trong một tam giác, tồn tại đường tròn đi qua các điểm nào sau đây:

A. Ba chân đường cao

B. Ba chân đường phân giác

C. Ba đỉnh của tam giác

D. Không câu nào đúng

Câu 15: Cho đường tròn tâm (O), ngoại tiếp tam giác ABC cân tại A. Gọi D và E lần lượt là trung điểm của AC và AB, còn G là trọng tâm của tam giác ABC. Tìm câu đúng:

A. E, G, D thẳng hàng

B. OG ⊥ BD

C. O là trực tâm tam giác BDG

D. A, B, C đều sai

Câu 16: Cho tam giác ABC vuông cân tại A có trọng tâm G. câu nào sau đây đúng:

A. Đường tròn đường kính BC đi qua O

B. AG = AB√2/6

C. BG qua trung điểm của AC

D. Không câu nào đúng

Câu 17: Cho nửa đường tròn đường kính AB trên đó có điểm C. Đường thẳng d vuông góc với OC tại C, Cắt AB tại E.Gọi D là hình chiếu của C lên AB. Tìm câu đúng:

A. EC² = ED.DO

B. CD² = OE.ED

C. OB² = OD.OE

D. CA = 1/2EO

Hướng dẫn giải và đáp án

Câu 8: Xét tam giác OAO’ ta thấy : OO’²=OA²+O’A²

Suy ra tam giác OAO’ vuông tại A.Gọi giao điểm của OO’ và AB là I.Xét tam giác vuông OAO’.

Theo hệ thức lượng ta có: AI.O O’= AO.AO’.Thay số ta tính được: AI=2,4cm

Vậy chọn đáp án A

Câu 9: Gọi I là giao điểm của OA và BC.Xét tam giác vuông OBA có: OA²=AB²+OB²

Thay số vào ta tình được AB= 2√3cm.

Câu 10:∠BAD = 130^o => sdBD = 2.130 = 260^o (góc nội tiếp đường tròn)

=> sdBAD = 360^o - 260^o = 100^o

=> ∠BOD = 100^o (góc ở tâm)

Chọn B

Câu 11: Diên tích hình tròn là S = πR²

Vì vậy Khi bán kính tăng 1,2 lần thì diện tích tăng 1,2² lần, tức là tăng 1,44 lần.

Câu 12: Xét tam giác vuông cân ABC.

Theo định lý Py-ta-go ta có: BC²=AB²+AC². Thay số ta tính được BC = 8√2

Vì tam giác ABC vuông tại A nên tam giác ABC nội tiếp đường tròn đường kính là BC nên bán kính BC : 2 = 4√2cm

Vậy chọn đáp án :D

Câu 13: Chọn đáp án :D

Câu 14: Đáp án: C

Câu 15: Đáp án: D

Câu 16: Đáp án: C

Câu 17: Xét tam giác vuông OCE có CD là đường cao hạ từ C.Theo hệ thức lượng ta có:

OC² = OD.OE

Mà OB = OC nên ta được: OB² = OD.OE

Vậy chọn C

Câu 18: Tứ giác MNPQ nội tiếp đường tròn, biết ∠P = 3∠M. Số đo góc P và góc M là:

A. ∠M = 45^o và ∠P = 135^o

B. ∠M = 60^o và ∠P = 120^o

C. ∠M = 30^o và ∠P = 90^o

D. ∠M = 45^o và ∠P = 90^o

Câu 19: Trong hình vẽ bên có: Tam giác ABC cân tại A và nội tiếp đường tròn tâm O, số đo góc BAC bằng 120. Khi đó số đo góc ACO bằng;

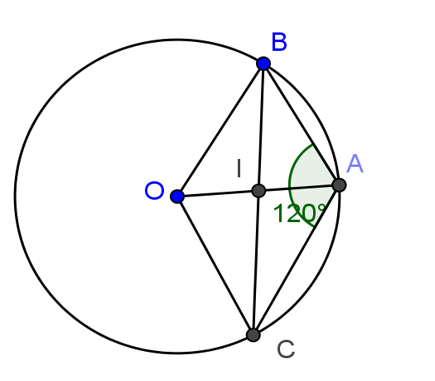
A. 120^o    B. 60^o     C. 45^o     D. 30^o

Câu 20: Cho tam giác ABC có diện tích bằng 1. Gọi M, N, P tương ứng là trung điểm của các cạnh AB, BC, CA và X, Y, Z tương ứng là trưng điểm của các cạnh PM, MN, NP. Khi đó diện tích tam giác XYZ là:

A. 1/4    B. 1/16    C. 1/32     D. 1/8

Câu 21: Tam giác đều có cạnh 8cm thì bán kính đường tròn nội tiếp tam giác là:

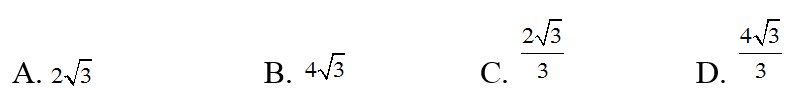
Câu 22: Trong tam giác ABC cân tại A, có ∠BAC = 30^o nội tiếp trong đường tròn (O). Số đo AB là;

A. 150^o     B. 165^o     C. 135^o     D. 160^o

Hướng dẫn giải và đáp án

Câu 18: Vì tứ giác MNPQ nội tiếp đường tròn nên ∠P + ∠M = 180^o mà ∠P = 3∠M

Suy ra ∠M = 45^o và ∠P = 135^o

Vậy chọn A

Câu 19: Ta có: ∠BAC = 120^o => sdBC = 240^o

Suy ra cung nhỏ BC = 360 - 240 = 120^o

Ta có tam giác ABC cân tại A với góc BAC = 120. Suy ra ∠ABI = ∠ACI = 30^o

Câu 20: Khi M,N,P là trung điểm của AB, BC, CA thì M, N, P chia tam giác ABC thành 4 tam giác bằng nhau

Suy ra diện tích của 4 tam giác này là bằng nhau và bằng 1/4. Khi X. Y, Z là trung điểm của 4 cạnh MP, MN, NP thì tam giác MNP chia thành 4 tam giác bằng nhau . Suy ra diện tích của tam giác XYZ bằng 1/4 diện tích tam giác MNP. Suy ra diện tích tam giác XYZ bằng 1/16 diện tích tam giác ABC.

Vậy chọn đáp án: B

Câu 21: Tâm đường tròn nội tiếp tam giác là trọng tâm G tam giác ABC.

Kẻ GI ⊥ AC. Khi đó CI = AC : 2 = 8 : 2 = 4cm.

Gọi D là trung điểm của AB.

CG = 2/3 CD = 2/3. 4√3 = 8√3/3 cm.

Xét tam giác vuông CGI . theo định lý py-ta-go ta có:

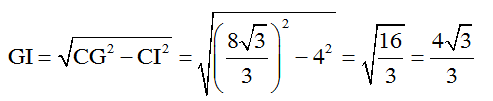
Vậy chọn đáp án: D

Câu 22: Vì tam giác ABC cân tại A có ∠BAC = 30^o=> ∠B = ∠C = 75^o

=> sdAB = 2∠C = 150^o (góc nội tiếp chắn nửa đường tròn bằng nửa đường tròn)

Câu 23: Trên đường tròn (O;R) lấy 3 điểm A, B sao cho AB=BC=R, M, N là trung điểm của 2 cung nhỏ AB và BC thì số đo góc ∠MBN là:

A. 120^o    B. 150^o    C. 240^o    D. 105^o

Câu 24: Tam giác ABC nội tiếp đường tròn(O) biết ∠C = 45^o và AB=a. Bán kính đường tròn (O) là:

A. a√2

B. a√3

C. a√2/2

D. a√3/3

Câu 25: Góc nội tiếp chắn nửa đường tròn là:

A. Góc vuông

B. Góc nhọn

C. Góc tù

D. Góc bẹt

Câu 26: Diện tích hình tròn là 64π thì chu vi của đường tròn là:

A. 64π    B. 8π    C. 32π    D. 16π

Câu 27: Chu vi của một đường tròn là 10π (cm) thì diện tích của hình tròn đó là:

A. 10π    B. 100π    C. 25π²;    D. 25π

Câu 28: Hai bán kính OA, OB của đường tròn (O) tạo thành góc AOB bằng 35^o. Số đo của góc tù tạo bởi hai tiếp tuyến tại A và B của (O) là:

A. 35^o    B. 55^o    C. 325^o    D. 145^o

Câu 29: Hai tiếp tuyến tại hai điểm A, B của đường tròn (O) cắt nhau tại M, tạo thành góc AMB bằng 50^o .Số đo của góc ở tâm chắn cung AB là:

A. 50^o    B. 40^o    C. 130^o    D. 310^o

Câu 30: Hình nào sau đây không nội tiếp đường tròn?

A. Hình vuông

B. Hình chữ nhật

C. Hình thoi

D. Hình thang cân

Câu 31: Hình vuông có diện tích 16(cm²) thì diện tích hình tròn nội tiếp hình vuông có diện tích là:

A. 4π (cm²)

B. 16π (cm²)

C. 8π (cm²)

D. 2π (cm²)

Hướng dẫn giải và đáp án

Câu 23: Vì AB = BC nên

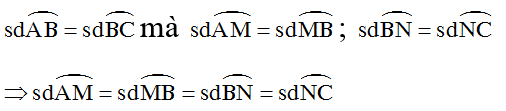
Ta có:

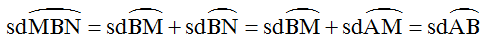
Vì tam giác ABC đều( vì AO=AB=OB) nên ∠AOB = 60^o

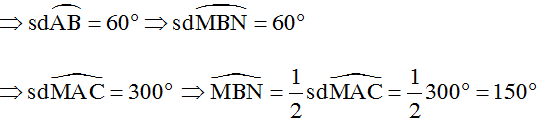
Vậy chọn đáp án: B

Câu 24: Vì ∠C = 45^o nên số đo cung nhỏ AB là 2 ∠C = 90^o.Suy ra ∠AOB = 90^o . Suy ra tam giác AOB vuông tại cân tai O. Áp dụng định lý py-ta go ta có vào tam giác AOB ta tính được: AO = a√2/2

Vậy chọn đáp án: C

Câu 25: Chọn đáp án: A

Câu 26: Chọn đáp án: D

Câu 27: Bán kính đường tròn là: R = 5

Diện tích đường tròn là: S = πR² = 25π

Câu 28: Đáp án: D vì 180^o - 35^o = 145^o

Câu 29: Ta có tứ giác AMBO nội tiếp đường tròn (vì có góc A + góc B= 180).

Suy ra ∠M + ∠O = 180^o => ∠O = 180^o - 50^o = 130^o

Vậy đáp án: C

Câu 30: Đáp án: D vì tổng 2 góc đối của hình thang cân không bằng 180.

Câu 31: Gọi (O;r) là đường tròn nội tiếp hình vuông

Gọi (O;R) là đường tròn ngoại tiếp hình vuông. Khi đó , ta có mối quan hệ giữa r và R là: r= R√2/2 và bán kính hình vuông là 2r.

Vì hình vuông có diện tích là 16(cm²) nên bán kính hình vuông là 4cm. Suy ra bán kính hình tròn nội tiếp hình vuông là: 4:2=2(cm).

Vậy diện tích hình tròn nội tiếp hình vuông là: (πR² = 4πcm²)

Chọn đáp án:A