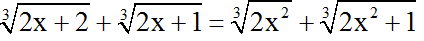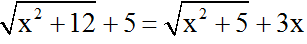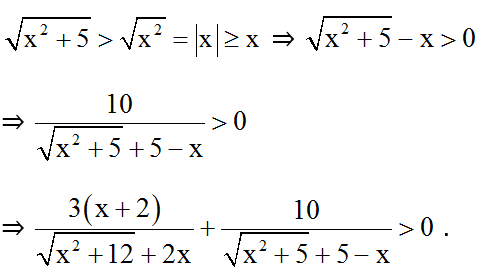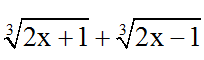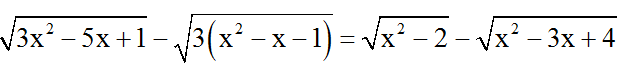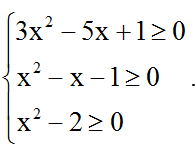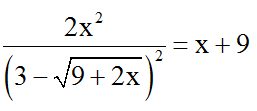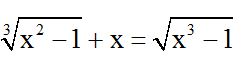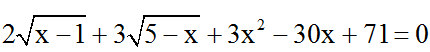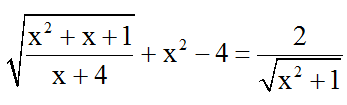Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay - Toán lớp 9
Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay
Với Cách giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình vô tỉ bằng phương pháp sử dụng biểu thức liên hợp từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
Phương pháp giải
Bước 1: Tìm đkxđ.
Bước 2: Nhẩm nghiệm (thường là nghiệm nguyên). Giả sử phương trình có nghiệm x = a
Bước 3: Tách, thêm bớt rồi nhân liên hợp sao cho xuất hiện nhân tử chung (x – a).
Các biểu thức liên hợp thường dùng:
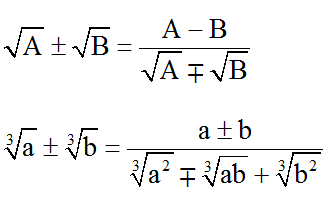
Bước 4. Chứng minh biểu thức còn lại luôn âm hoặc dương
Bước 5. Đối chiếu điều kiện, kết luận nghiệm.
Ví dụ minh họa
Ví dụ 1: Giải phương trình: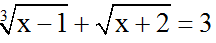 
Hướng dẫn giải:
Phân tích: Để ý thấy x = 2 là nghiệm của phương trình, do đó ta có thể liên hợp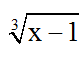 
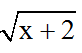
và 1; 
và 2.
Đkxđ: x ≥ -2 .
Ta có:
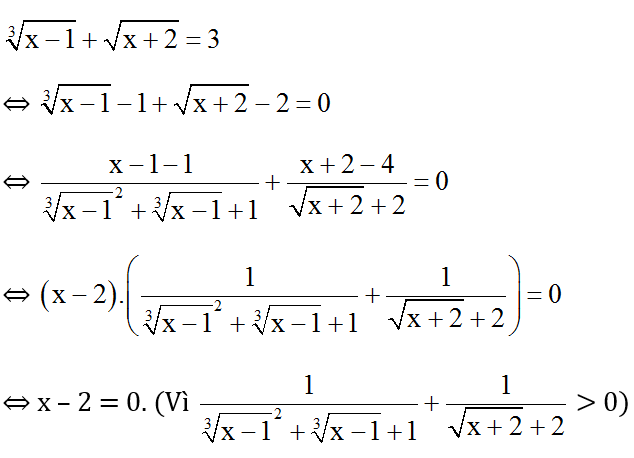
⇔ x = 2 (t.m đkxđ)
Vậy phương trình có nghiệm x = 2.
Ví dụ 2: Giải phương trình: 
Hướng dẫn giải:
Đkxđ: ∀ x ∈ R
Ta có:
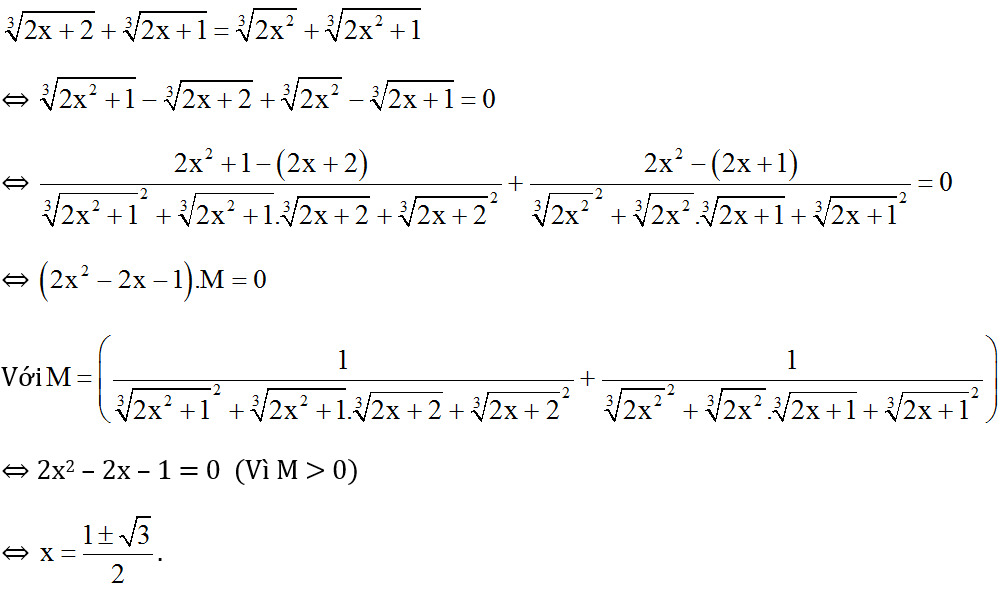
Vậy phương trình có hai nghiệm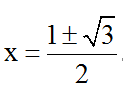 
.
Ví dụ 3: Giải phương trình 
Hướng dẫn giải:
Gợi ý: Nhẩm được phương trình có nghiệm x = 2 nên ta tách các biểu thức để liên hợp sao cho xuất hiện nhân tử (x – 2).
Đkxđ: ∀ x ∈ R
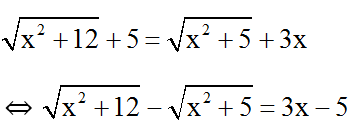
Vì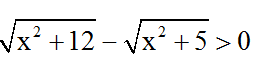 
nên phương trình có nghiệm ⇔ 3x - 5 > 0 ⇔ x > 5/3 .
Khi đó:
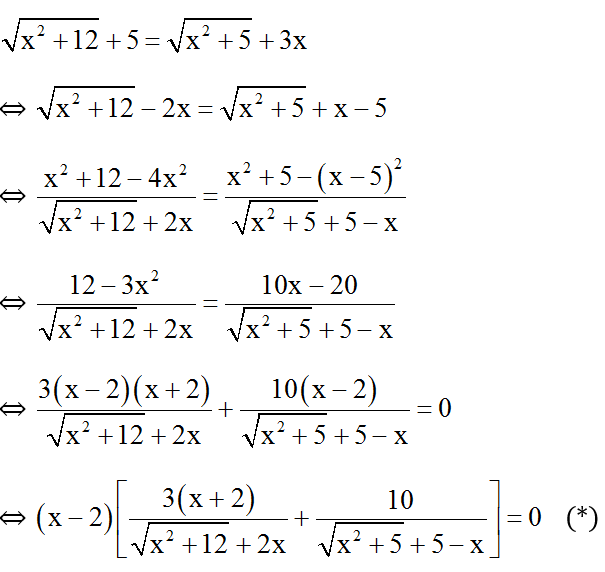
Với x > 5/3 > 0 thì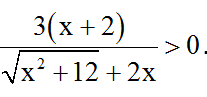 
.
Lại có 
(*) ⇔ x – 2 = 0 ⇔ x = 2.
Vậy phương trình có nghiệm x = 2.
Bài tập trắc nghiệm tự luyện
Bài 1: Biểu thức liên hợp của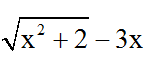 
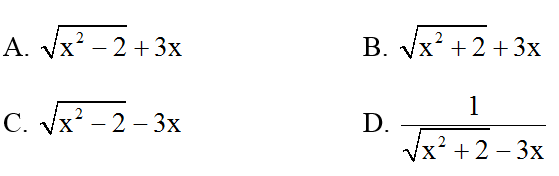
là:
Lời giải:
Đáp án: B
Bài 2: Biểu thức liên hợp của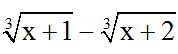 
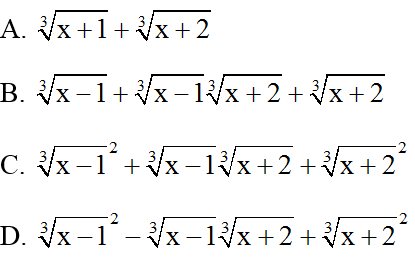
là:
Lời giải:
Đáp án: C
Bài 3: Biểu thức nào dưới đây bằng với biểu thức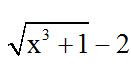 
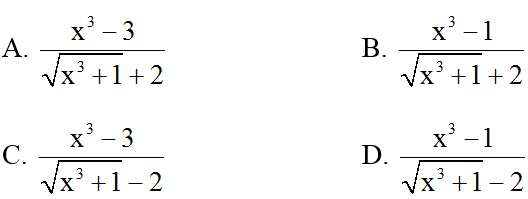
Lời giải:
Đáp án: A
Bài 4: Biểu thức nào dưới đây bằng với biểu thức 
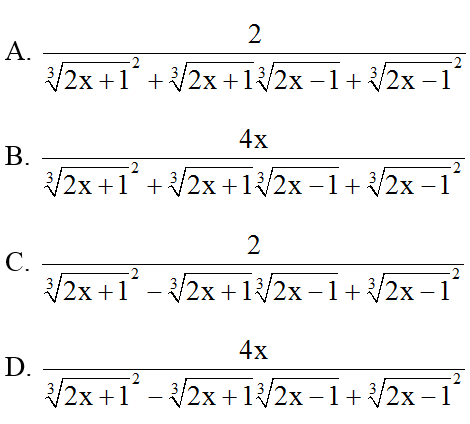
Lời giải:
Đáp án: D
Bài 5: Nghiệm của phương trình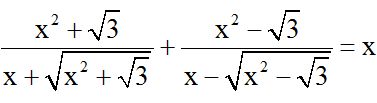 
có nghiệm là:
A. x = √2 B. x = -√2
C. x = √3 D. x = -√3
Lời giải:
Đáp án: A
Bài 6: Giải phương trình 
Hướng dẫn giải:
Đkxđ: 
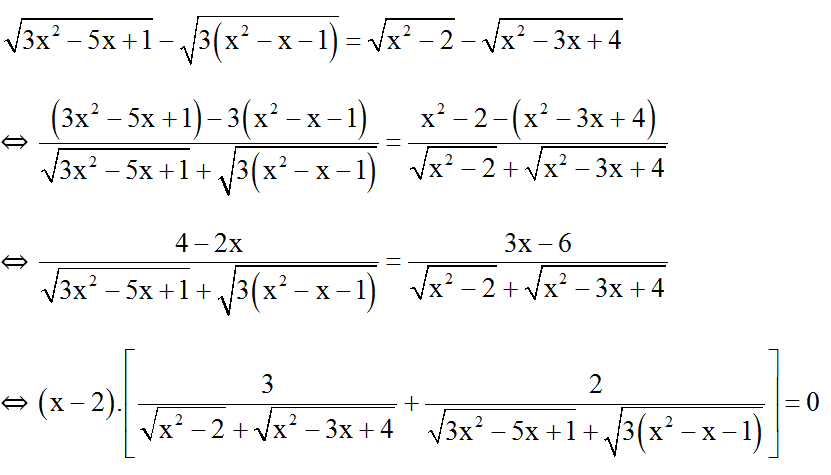
⇔ x – 2 = 0 (Vì biểu thức trong [...] luôn dương)
⇔ x = 2 (t.m đkxđ).
Vậy phương trình có nghiệm x = 2.
Bài 7: Giải phương trình 
Hướng dẫn giải:
Đkxđ: x ≥ -9/2; x ≠ 0 .
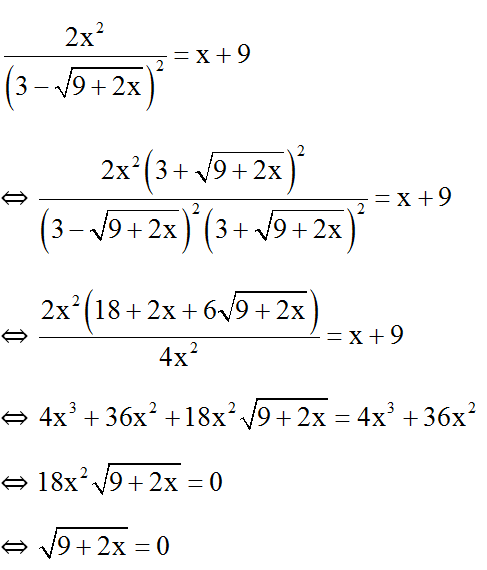
⇔ x = -9/2 (t.m đkxđ).
Vậy phương trình có nghiệm x = -9/2 .
Bài 8: Giải phương trình 
Hướng dẫn giải:
Đkxđ: x ≥ 1.
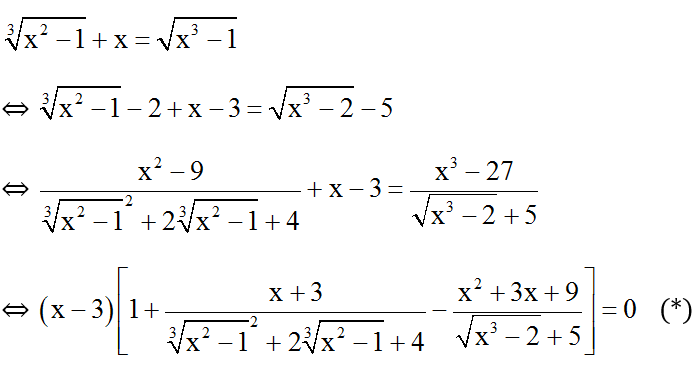
Ta chứng minh được:
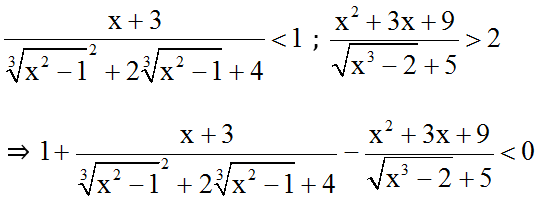
Khi đó (*) ⇔ x – 3 = 0 ⇔ x = 3 (t.m đk xđ).
Vậy phương trình có nghiệm x = 3.
Bài 9: Giải phương trình: 
Hướng dẫn giải:
Đkxđ: 1 ≤ x ≤ 5 .
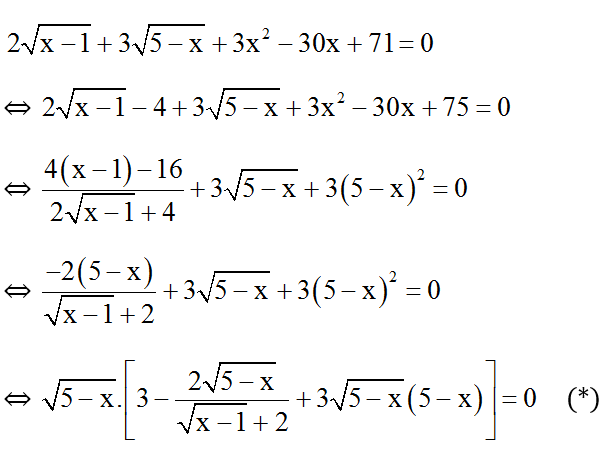
Ta thấy: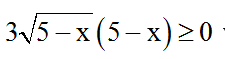 
với 1 ≤ x ≤ 5 .
Ta chứng minh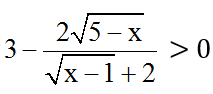 
Thật vậy: Với 1 ≤ x ≤ x thì: 
(*) ⇔ 
⇔ x = 5 (t.m đkxđ).
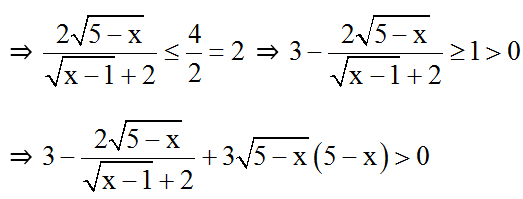
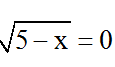
Vậy phương trình có nghiệm x = 5.
Bài 10: Giải phương trình: 
Hướng dẫn giải:
Đkxđ: x > -4.
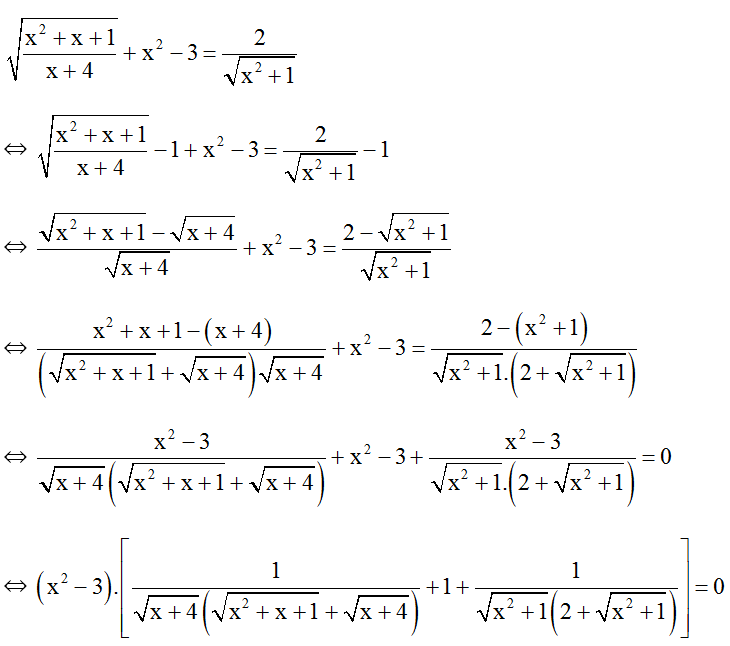
⇔ x2 - 3 = 0(Vì biểu thức trong [ ] luôn dương)
⇔ x2 = 3
⇔ x = ±√3(t.m đkxđ).
Vậy phương trình có hai nghiệm x = ±√3 .
