Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C
Câu hỏi:
Cho đường tròn (O; R) đường kính AB. Điểm C thuộc đường tròn sao cho AC > CB, C khác A và B. Kẻ CH vuông góc với AB tại H; kẻ OI vuông góc với AC tại I. Gọi giao điểm BM với CH là K. Chứng minh tam giác AMO đồng dạng với tam giác HCB và KC = KH.
Trả lời:
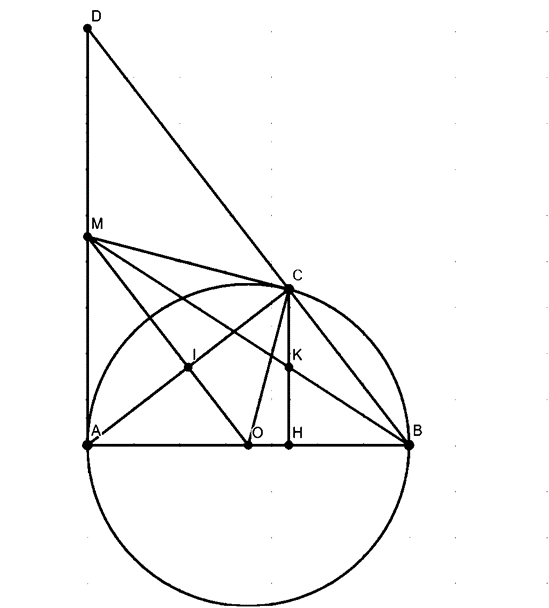
Gọi BC giao AM tại D
Ta có: OI ⊥ AC nên OI // CB (CB ⊥ AC vì \(\widehat {ACB} = 90^\circ \)là góc nội tiếp chắn nửa đường tròn)
Suy ra: OM // BD
Mà O là trung điểm AB nên OM là đường trung bình của tam giác ABD
Suy ra: M là trung điểm AD hay MA = MD
Có: OM // BD nên \(\widehat {MOA} = \widehat {CBH}\)(2 góc đồng vị)
Xét ∆AMO và ∆HCB có:
\(\widehat {MAO} = \widehat {CHB} = 90^\circ \)(Vì AD là tiếp tuyến nên AM ⊥ AO)
\(\widehat {MOA} = \widehat {CBH}\)
Suy ra: ∆AMO ∽ ∆HCB (g.g.)
Lại có: AD là tiếp tuyến của (O) nên: AD ⊥ AB
Mà CH ⊥ AB
Suy ra: AD // CH
Áp dụng định lý Ta–lét trong tam giác DBM có CK // DM:
\(\frac{{CK}}{{DM}} = \frac{{BK}}{{BM}}\)(1)
Áp dụng định lý Ta–lét trong tam giác BMA có HK// MA:
\(\frac{{HK}}{{MA}} = \frac{{BK}}{{BM}}\)(2)
Từ (1) và (2) suy ra: \(\frac{{CK}}{{DM}} = \frac{{HK}}{{MA}}\)
Mà DM = DA nên KC = KH.

