70 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 65)
Haylamdo biên soạn và sưu tầm 70 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
70 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 65)
Câu 1:
Câu 2:
Khẳng định nào sau đây sai?
Câu 3:
Câu nào trong các câu sau không phải là mệnh đề?
Câu 4:
Cho hình thang ABCD vuông góc tại A và B, có AD = 2a, AB = BC = a. Trên tia Ax vuông góc với mặt phẳng (ABCD) lấy một điểm S. Gọi C’, D’ lần lượt là hình chiếu vuông góc của A trên SC và SD. Chứng minh rằng .
Câu 5:
Cho hình thang ABCD vuông tại A và B với . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
Câu 6:
Cho hàm số (1). Viết phương trình tiếp tuyến của đồ thị hàm số (1), biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt A, B và tam giác OAB cân tại gốc tọa độ 0.
Câu 7:
Trong không gian Oxyz, cho điểm P(a;b;c). Tính khoảng cách từ điểm P đến trục tọa độ Oy.
Câu 11:
Với các chữ số 0; 1; 2; 3; 4; 5 ta lập được bao nhiêu số có 8 chữ số mà trong đó chữ số 1 có mặt 3 lần, các chữ số còn lại có mặt đúng 1 lần?
Câu 12:
Từ các chữ số 0; 1; 2; 3; 4 có thể lập được bao nhiêu số:Có 8 chữ số trong đó chữ số 1có mặt 3 lần, chữ số 4 xuất hiện 2 lần; các chữ số còn lại có mặt đúng một lần.
Câu 14:
Cho (O) đường kính AB. Lấy C thuộc (O), gọi E là trung điểm BC. Tiếp tuyến tại C của (O) cắt OE ở D. Chứng minh: ΔACB vuông và OE ⊥ BC.
Câu 15:
Cho đường tròn tâm O có đường kính AB và C là một điểm thuộc đường tròn tâm O (C khác A, B). Lấy điểm D thuộc dây cung BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F. Chứng minh tứ giác FCDE nội tiếp.
Câu 20:
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số: f(x) = 2x3 + 3x2 − 1trên đoạn . Tính P = M − m.
Câu 21:
Cho hình phẳng (H) giới hạn bởi đường parabol (P): y = x2 − x + 2 và tiếp tuyến của đồ thị hàm số y = x2 + 1 tại điểm có tọa độ (1; 2). Tính diện tích của hình (H).
Câu 26:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy. Biết thể tích khối chóp S.ABCD bằng . Gọi α là góc giữa SC và mặt đáy. Tính tan α.
Câu 27:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh , cạnh bên SA vuông góc với mặt đáy. Mặt phẳng (α) qua A và vuông góc với SC cắt các cạn SB, SC, SD lần lượt tại các điểm M, N, P. Tính thể tích V của khối cầu ngoại tiếp tứ diện CMNP.
Câu 28:
Cho hình nón có thiết diện qua trục là tam giác đều. Gọi V1 , V2 lần lượt là thể tích của khối cầu nội tiếp và nội tiếp hình nón đã cho. Tính .
Câu 30:
Tìm giá trị nhỏ nhất của hàm số y = x4 − 4x3 − x2 + 10x – 3 trên đoạn [−1; 4].
Câu 31:
Cho điểm M thuộc nửa đường tròn (O ;R), đường kính AB (M khác A và B). Gọi E và F lần lượt là trung điểm của MA và MB. Chứng minh rằng tứ giác MEOF là hình chữ nhật.
Câu 32:
Cho nửa đường tròn tâm O bán kính R đường kính AB. Gọi Ax By là các tia tiếp tuyến của nửa đường tròn và thuộc cùng 1 nửa mặt phẳng có chứa nửa đường tròn. Qua M thuộc nửa đường tròn vẽ tiếp tuyến với nửa đường tròn cắt Ax, By lần lượt tại C, D. Chứng minh rằng AC. BD = R2.
Câu 33:
Một chiếc bút chì có dạng khối lăng trụ lục giác đều có cạnh đáy 3 mm và chiều cao bằng 200 mm. Thân bút chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng khối trụ có chiều cao bằng chiều dài của bút và đáy là hình tròn có bán kính 1 mm. Giả định 1 m3 gỗ có giá a triệu đồng, 1 m3 than chì có giá 6a triệu đồng. Tính giá nguyên vật liệu làm một chiếc bút chì như trên.
Câu 34:
Một túi chứa 6 viên bi trắng và 5 viên bi xanh. Lấy ra 4 viên bi từ túi đó, có bao nhiêu cách lấy được 4 viên bi cùng màu?
Câu 35:
Một hộp đựng 15 viên bi khác nhau gồm 4 bi đỏ, 5 bi trắng và 6 bi vàng. Tính số cách chọn 4 viên bi từ hộp đó sao cho không có đủ 3 màu.
Câu 41:
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Góc giữa CA’ và mặt (AA’B’B) bằng 30o. Tính thể tích khối lăng trụ ABC.A’B’C’.
Câu 42:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V.
Câu 43:
Cho hình nón N1 có chiều cao bằng 40 cm. Người ta cắt hình nón N1 bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ N2 có thể tích bằng 18 thể tích N1. Tính chiều cao của hình nón N2.
Câu 44:
Cho hàm số y = f(x) có đạo hàm f'(x) = x2(x − 1)(x + 2)2(x − 2). Tìm số điểm cực trị của hàm số đã cho.
Câu 47:
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình vẽ bên. Xác định dấu của a, b và c.
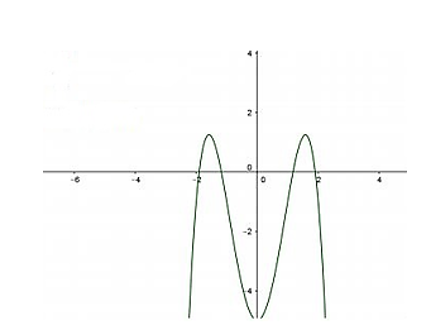
Câu 48:
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Gọi I, J lần lượt là trung điểm hai cạnh AA′ và BB′. Tính thể tích của khối đa diện ABCIJC′.
Câu 49:
Cho khối lăng trụ tam giác ABC.A′B′C′ có thể tích là V. Tính thể tích khối chóp A.BCC’B’.
Câu 52:
Từ các số: 5; 2; 6; 8; 0.
a) Có thể viết được bao nhiêu số có ba chữ số?
b) Có thể viết được bao nhiêu số chẵn có ba chữ số?
Câu 53:
Cho các chữ số 2; 4; 1; 6; 9. Hỏi:
a) Có bao nhiêu số có 3 chữ số được lập từ các chữ số trên?
b) Có bao nhiêu số có 3 chữ số khác nhau được lập từ các chữ số trên?
Câu 55:
Cho hàm số: y = x−4. Tìm khẳng định sai.
B. Đồ thị hàm số đi qua điểm (1; 1)
Câu 56:
Biết rằng y = f(x) là một hàm số lẻ trên tập xác định D. Khẳng định nào sai?
Câu 57:
Cho một đa giác (H) có 60 đỉnh nội tiếp một đường tròn (O). Người ta lập một tứ giác tùy ý có bốn đỉnh là các đỉnh của (H). Tính xác suất để lập được một tứ giác có bốn cạnh đều là đường chéo của (H).
Câu 60:
Trong mặt phẳng với hệ trục tọa độ Oxy cho đường tròn (C1): x2 + y2 − 2x − 2y – 2 = 0 và (C2): x2 + y2 + 12x − 16y = 0. Phép đồng dạng F tỉ số k biến (C1) thành (C2). Tìm k.
Câu 61:
Với các chữ số 0, 2, 3, 5, 6, 7, 9. Lập được bao nhiêu số có 10 chữ số mà trong mỗi số chữ số 5 có mặt đúng 3 lần, chữ số 6 có mặt đúng 2 lần và các chữ số khác, mỗi chữ số có mặt đúng 1 lần?
Câu 62:
Cho hình bình hành ABCD. Lấy các điểm M, N, P thỏa mãn . Đặt . Biểu diễn vectơ theo
Câu 63:
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
Câu 64:
Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Tìm P là giao điểm của SC và (ADN).
Câu 65:
Cho khối lăng trụ ABC.A’B’C’, khoảng cách từ c đến BB′ là , khoảng cách từ A đến BB’ và CC′ lần lượt là 1; 2. Hình chiếu vuông góc của A lên mặt phẳng (A’B’C’) là trung điểm M của B’C’, . Tính thể tích của khối lăng trụ đã cho.
Câu 70:
Cho tứ diện ABCD, có AB = CD = 5, khoảng cách giữa AB và CD bằng 12, góc giữa hai đường thẳng AB và CD bằng 30°. Tính thể tích khối tứ diện ABCD.

