101 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 72)

Cho hai tập hợp X = {1; 2; 3; 4}; Y = {1;2}. Tập hợp C_XY là tập hợp nào sau đây?

A. {3; 4}.

B. {1; 2; 3; 4}.

C. {1; 2}.

D. ∅.

Nghiệm của phương trình cos x + sin x = 0 là:

A. \(x = - \frac{\pi }{4} + k\pi .\)

B. \(x = \frac{\pi }{6} + k\pi .\)

C. \(x = k\pi .\)

D. \(x = \frac{\pi }{4} + k\pi .\)

Giá trị của biểu thức A=tan1°tan2°tan3°...tan88°tan89° là:

A. 3.

B. 0.

C. \[\frac{{\sqrt 2 }}{2}.\]

D. 1.

Giá trị của tan 45° + cot 135° bằng bao nhiêu?

A. 2.

B. 0.

C. \[\sqrt 3 .\]

D. 1.

Số cực trị của hàm số \[y = \frac{{ax + b}}{{cx + d}}\] là:

A. 0

B. 1

C. 2

D. 3

Cho hàm số y = x⁴ − 2x² + 2m + 1 (C_m).

Tìm m để (C_m)  cắt trục Ox tại 4 điểm phân biệt có hoành độ lập thành cấp số cộng.

Với giá trị nào của tham số m thì phương trình \[{\left( {2 + \sqrt 3 } \right)^x} + {\left( {2 - \sqrt 3 } \right)^x} = m\] vô nghiệm.

Có bao nhiêu phép tịnh tiến biến hình vuông thành chính nó?

A. 0.

B. 1.

C. 2.

D. 3.

Tìm x biết: (2x + 1)³ ‒ 1 = ‒344

Cho biết 3cosα − sinα = 1, 0 < α < 90°. Giá trị của tanα bằng:

A. \[\tan \alpha = \frac{4}{3}.\]

B. \[\tan \alpha = \frac{3}{4}.\]

C. \[\tan \alpha = \frac{4}{5}.\]

D. \[\tan \alpha = \frac{5}{4}.\]

Trong mặt phẳng tọa độ Oxy cho đường tròn (C'): x² + y² ‒ 10x ‒ 2y + 23 = 0 và đường thẳng d: x ‒ y + 2 = 0, phương trình đường tròn (C') là ảnh của đường tròn (C) qua phép đối xứng trục d là:

A. (C′): x² + y² + 4x − 12y + 26 = 0

B. (C′): x² + y2 + 2x − 14y + 47 = 0

C. (C′): x² + y² + 8x − 6y + 53 = 0

D. (C′): x² + y² + 2x − 6y + 12 = 0

Tìm giao điểm 2 đường tròn x² + y² = 5 và C2: x² + y² − 4x − 8y + 15 = 0

A. (1; 2) và \(\left( {\sqrt 2 ;\sqrt 3 } \right)\).

B. (1; 2).

C. (1; 2) và \(\left( {\sqrt 3 ;\sqrt 2 } \right)\).

D. (1; 2) và (2; 1).

Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây sai?

A. \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OE} = 0.\)

B. \(\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AD} \).

C. \(\overrightarrow {OA} + \overrightarrow {OC} + \overrightarrow {OB} = \overrightarrow {EB} .\)

D. \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EF} = 0.\)

Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.

+ Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu;

+ Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.

Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

A. 5 lít nước cam và 4 lít nước táo.

B. 6 lít nước cam và 5 lít nước táo.

C. 4 lít nước cam và 5 lít nước táo.

D. 4 lít nước cam và 6 lít nước táo.

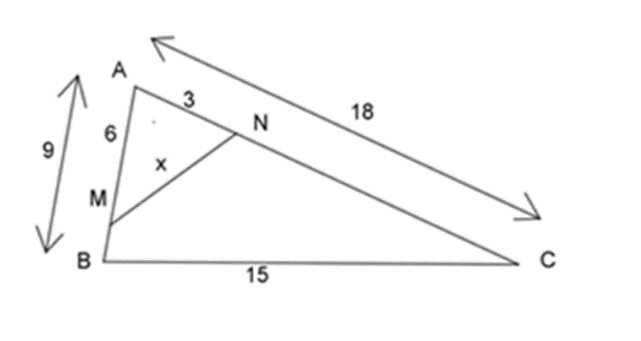
Cho tam giác ABC có trọng tâm G và hai trung tuyến AM, BN. Biết AM=15, BN = 12 và tam giác CMN có diện tích là \[15\sqrt 3 \]. Tính độ dài đoạn thẳng MN

Cho tứ diện ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. Tính thể tích V của khối chóp A.GBC

A. V = 3.

B. V = 4.

C. V = 5.

D. V = 6.

Cho hai tập hợp E = {x ∈ ℝ: f(x) = 0}; F = { x ∈ ℝ: g(x) = 0}; H = {x ∈ ℝ: f(x).g(x) = 0}. Trong các mệnh đề sau, mệnh đề đúng là:

A. H = E ∪ F.

B. H = E ∩ F

C. H = E \ F.

Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I . Đường thẳng qua I và vuông góc với IA cắt OB tại K. Chọn khẳng định đúng.

A. OI = OK = KI.

B. KI = KO.

C. OI = OK.

D. IO = IK.

Hai tiếp tuyến tại A và B của đường tròn (O;R) cắt nhau tại M. Nếu \[MA = R\sqrt 3 \] thì góc góc (AOB) bằng:

A. 120°.

B. 90°.

C. 60°.

D. 45°.

Phép vị tự nào sau đây biến đường tròn (C): (x ‒ 3)² + (y ‒ 1)² = 4 thành đường tròn (C’): (x ‒ 5)² + (y ‒ 3)² = 4

A. V_{(I; ‒1)} với I (4; 2).

B. V_{(I; 1)} với I (1; 1).

C. V_{(I; ‒1)} với I (1; 1).

D. V_{(I; 1)} với I (4; 2).

Tập nghiệm của phương trình \[2x + \frac{3}{{x - 1}} = \frac{{3x}}{{x - 1}}\] là:

A. \[S = \left\{ {1;\frac{3}{2}} \right\}.\]

B. S = {1}.

C. \[S = \left\{ {\frac{3}{2}} \right\}.\]

D. ∅.

Tìm các giá trị của m để hàm số y = ‒x³ + (m + 3)x² ‒ (m² + 2m)x ‒ 2 đạt cực đại tại x = 2.

Cho tứ giác ABCD. Trên cạnh AB; CD lấy lần lượt các điểm M, N sao cho \(3\overrightarrow {AM} = 2\overrightarrow {AB} \) và \(3\overrightarrow {DN} = 2\overrightarrow {DC} \). Tính vectơ \(\overrightarrow {MN} \) theo hai vectơ \(\overrightarrow {AD} ,\overrightarrow {BC} \).

A. \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {BC} \)

B. \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AD} - \frac{2}{3}\overrightarrow {BC} \).

C. \(\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BC} \)

D. \(\overrightarrow {MN} = \frac{2}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {BC} \)

Cho tứ giác ABCD gọi M,N là hai điểm di động trên AB,CD sao cho \[\frac{{MA}}{{MB}} = \frac{{ND}}{{NC}}\] và I, J lần lượt là trung điểm của AD, BC.

a, Tính vecto IJ theo vecto AB, DC.

b, Chứng minh trung điểm P của MN nằm trên đường thẳng IJ.

Cho hai đường thẳng d và d’ song song có bao nhiêu phép tịnh tiến biến đường thẳng d thành đường thẳng d’:

A. Không có phép tịnh tiến nào.

B. Có duy nhất 1 phép tịnh tiến.

C. Có 2 phép tịnh tiến.

D. Có vô số phép tịnh tiến.

Đường tròn nội tiếp hình vuông cạnh a có bán kính là:

A. \[a\sqrt 2 .\]

B. \[\frac{{a\sqrt 2 }}{2}.\]

C. \[\frac{a}{2}.\]

D. \[\frac{{a\sqrt 3 }}{2}.\]

Mặt cầu tâm I(0; 0; 1) bán kính \[R = \sqrt 2 \] có phương trình:

A. \[{x^2} + {\rm{ }}{y^2} + {\rm{ }}{\left( {z - 1} \right)^2} = \sqrt 2 .\]

B. \[{x^2} + {\rm{ }}{y^2} + {\rm{ }}{\left( {z + 1} \right)^2} = \sqrt 2 .\]

C. x² + y² + (z ‒ 1)² = 2.

D. x² + y² + (z + 1)² = 2.

Hàm số \(y = \sqrt[5]{{{{\left( {{x^2} + 1} \right)}^2}}}\) có đạo hàm là:

A. \(y' = \frac{4}{{\sqrt[5]{{{{\left( {{x^2} + 1} \right)}^2}}}}}.\)

B. \(y' = 2x\sqrt {{x^2} + 1} .\)

C. \(y' = 4x\sqrt[5]{{{x^2} + 1}}.\)

D. \(y' = \frac{{4x}}{{5\sqrt[5]{{{{\left( {{x^2} + 1} \right)}^3}}}}}.\)

Cho các tập hợp khác rỗng A = (‒∞; m) ) và B = [2m ‒ 2; 2m + 2]. Tìm m ∈ ℝ để C_ℝA ∩ B ≠ ∅.

A. m ≥ 2.

B. m < ‒2.

C. m ≥ ‒2.

D. m < 2.

Cho hai tập khác rỗng A = (m ‒ 1; 4) ]; B = (‒2; 2m + 2) ,m ∈ ℝ. Tìm m để A ∩ B ≠ ∅.

A. ‒2 < m < 5.

B. m > ‒3.

C. ‒1< m < 5.

D. 1 < m < 5.

Cho đường tròn (C) có phương trình (x − 2)² + (y − 2)² = 4, thực hiện lần lượt phép vị tự tâm O tỉ số k = 2 và phép quay tâm O góc (90°) biến đường tròn (C) thành đường tròn nào ?

A. (x + 2)² + (y ‒ 1)² = 16.

B. (x ‒ 1)² + (y ‒ 1)² = 16.

C. (x + 4)² + (y ‒ 4)² = 16.

D. (x ‒ 2)² + (y ‒ 2)² = 16.

Cho các số dương x, y, z thỏa mãn xyz = 1. Khi đó giá trị nhỏ nhất của biểu thức \(P = \frac{{\sqrt {1 + {x^3} + {y^3}} }}{{xy}} + \frac{{\sqrt {1 + {y^3} + {z^3}} }}{{yz}} + \frac{{\sqrt {1 + {z^3} + {x^3}} }}{{zx}}\) là:

A. \(3\sqrt[3]{3}\).

B. \(3\sqrt 3 \).

C. \(\frac{{3\sqrt[3]{3}}}{2}\).

D. \(\frac{{3\sqrt 3 }}{2}\).

Gọi B_n là tập hợp bội số của n trong tập Z các số nguyên. Sự liên hệ giữa m và n sao cho B_n ∩ B_m = B_mn là:

A. m là bội số của n,

B. n là bội số của m.

C. m, n nguyên tố cùng nhau.

D. m, n đều là số nguyên tố.

Cho hình chữ nhật tâm O. Hỏi có bao nhiêu phép quay tâm O góc α với 0 ≤ α < 2π, biến hình chữ nhật trên thành chính nó?

A. 0.

B. 2.

C. 3.

D. 4.

Cho hình chữ nhật tâm O. Hỏi có bao nhiêu phép quay tâm O góc α với 0 < α < 2π, biến hình chữ nhật trên thành chính nó?

A. 0.

B. 1.

C. 2.

D. vô số.

Có 6 học sinh và 3thầy giáo A, B, C ngồi trên một hàng ngang có 9 ghế. Số cách xếp chỗ ngồi cho 9 người đó sao cho mỗi thầy giáo ngồi giữa hai học sinh là:

A. 43 200.

B. 94 536.

C. 55 012.

D. 35 684.

Cho hàm số f(x) = x³ + (m² + 1)x + m² ‒ 2 với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 2] bằng 7.

Cho hàm số \[f\left( x \right) = \frac{{x - {m^2} + m}}{{x + 1}}\] với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có giá trị nhỏ nhất trên đoạn [0; 1] bằng ‒2.

Tìm m để phương trình cos2x ‒ (2m − 1)cosx ‒ m + 1 = 0 có đúng 2 nghiệm \[x \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right].\]

A. ‒1 < m ≤ 0.

B. 0 ≤ m < 1.

C. 0 ≤ m ≤ 1.

D. ‒1 < m < 1.

Định m để phương trình mcos²x− 4sinxcosx + m − 2 = 0 có nghiệm trong khoảng \[x \in \left( {0;\frac{\pi }{4}} \right)\]

A. \[1 < m < \frac{8}{3}.\]

B. 0 ≤ m ≤ 3.

C. 0 < m < 1.

D. m ∈ (‒∞; 0] ∪ [1; +∞) \{2}.

Tìm nguyên hàm của hàm số f(x) = sin²x

A. \(\int {f\left( x \right)dx = \frac{1}{2}x + \frac{1}{4}{\rm{sin}}2x + C} \)

B. \(\int {f\left( x \right)dx = - \frac{1}{2}x + \frac{1}{4}{\rm{sin}}2x + C} \)

C. \(\int {f\left( x \right)dx = - \frac{1}{2}x - \frac{1}{4}{\rm{sin}}2x + C} \)

D. \(\int {f\left( x \right)dx = \frac{1}{2}x - \frac{1}{4}{\rm{sin}}2x + C} \)

Số nghiệm của phương trình \[\sin 5x + \sqrt 3 cos5x = 2\sin 7x\] trên khoảng \[\left( {0;\frac{\pi }{2}} \right)\] là:

A. 4.

B. 1.

C. 3.

D. 2.

Biết n là số nguyên dương thỏa mãn \[3C_{n + 1}^3 - 3A_n^2 = 52\left( {n - 1} \right).\] Giá trị của n bằng:

A. 13.

B. 16.

C. 15.

D. 14.

Giải phương trình sinxcosx + 2(sinx + cosx) = 2

A. \(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k\pi }\\{x = k\pi }\end{array},k \in \mathbb{Z}} \right.\).

B. \(\left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k2\pi }\\{x = k2\pi }\end{array},k \in \mathbb{Z}} \right.\).

C. \(\left[ {\begin{array}{*{20}{l}}{x = - \frac{\pi }{2} + k2\pi }\\{x = k2\pi }\end{array},k \in \mathbb{Z}} \right.\).

D. \(\left[ {\begin{array}{*{20}{l}}{x = - \frac{\pi }{2} + k2\pi }\\{x = k\pi }\end{array},k \in \mathbb{Z}} \right.\).

Trong hình vẽ bên có đồ thị các hàm số y = a^x; y = b^x; y = log_cx. Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?

A. a < c < b

B. c < a < b

C. a < b = c

D. b < c < a

Cho hàm số y = f(x) có đạo hàm f'(x) = (x ‒ 1)(x² ‒ 2)(x⁴ ‒ 4). Số điểm cực trị của hàm số y = f(x) là:

A. 3

B. 2

C. 4

D. 1

Cho hàm số f(x) có đạo hàm là f′(x)=x(x + 1)²(x − 2)⁴ với mọi x ∈ ℝ. Số điểm cực trị của hàm số f(x) là:

A. 0

B. 3

C. 2

D. 1

Hình vẽ bên là đồ thị của hàm số \[y = \frac{{ax + b}}{{cx + d}}\]

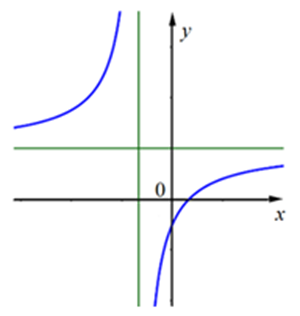
Mệnh đề nào đúng?

A. ad > 0 và bd > 0.

B. ad > 0 và ab < 0.

C. bd < 0 và ab > 0.

D. ad < 0 và ab < 0.

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt bên SAB là tam giác đều cạnh \[\sqrt 3 a\],ABC là tam giác vuông tại A có cạnh AC = a, góc giữa AD và (SAB) bằng 30°. Thể tích khối chóp S.ABCD  bằng: 

A. \({a^3}\)

B. \(\frac{{\sqrt 3 {a^3}}}{6}\)

C. \(\frac{{\sqrt 3 {a^3}}}{2}\)

D. \(\frac{{\sqrt 3 {a^3}}}{4}\)

A. \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 2 }}{2}.\)

B. \({S_{\Delta ABC}} = {a^2}\sqrt 2 .\)

C.\({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 2 }}{4}.\)

D. \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 2 }}{6}.\)

Trong mặt phẳng Oxy cho đường thẳng ∆ : x − y + 4 = 0. Trong bốn đường thẳng cho bởi các phương trình sau đường thẳng có thể biến thành ∆ qua một phép đối xứng tâm là:

A. 2x + y ‒ 4 = 0

B. 2x + 2y ‒ 3 = 0

C. 2x ‒ 2y + 1 = 0

D. x + y ‒ 1 = 0

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x³ ‒ 3x² ‒ 9x + 35 trên đoạn [‒4; 4]. Giá trị của M và m lần lượt là

A. M = 40; m = 8.

B. M = 40; m = ‒41.

C. M = 15; m = ‒41.

D. M = 40; m = ‒8.

Giá trị nhỏ nhất Fmin của biểu thức F(x; y) = y − x trên miền xác định

\[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\] là

A. F_min = 1 khi x = 2, y = 3.

B. F_min = 2 khi x = 0, y = 2.

C. F_min = 3 khi x = 1, y = 4.

D. F_min = 4 khi x = 0, y = 0.

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, cạnh AC = 2, \[\widehat {BAC} = 30^\circ ,\] SA vuông góc với đáy và SA = A. Tính thể tích khối chóp S.ABC và tính khoảng cách giữa hai đường thẳng SB với AC.

Xác định tính đúng sai của mệnh đề đảo của các mệnh đề sau:

Nếu x > y thì x³ > y³.

Gọi S là tổng tất cả các nghiệm thuộc [0; 30π] của phương trình 2cos²x + sin x ‒ 1 = 0. Khi đó, giá trị của S bằng:

A. \(S = \frac{{1365}}{2}\pi \).

B. \(S = \frac{{1215}}{2}\pi \).

C. S = 622π.

D. \(S = \frac{{1335}}{2}\pi \).

Cho A = [1; 4], B = (2; 6), C = (1; 2). Tìm A ∩ B ∩ C.

A. [0; 4].

B. [5; +∞).

C. (‒∞; 1).

D. ∅

Đạo hàm của hàm số \[y = \frac{1}{{{x^2}}}\] là:

A. \[ - \frac{1}{{{x^3}}}.\]

B. \[ - \frac{1}{x}.\]

C. \[ - \frac{2}{{{x^3}}}.\]

D. \[ - \frac{1}{{{x^4}}}.\]

Cho hai đa thức f(x) và g(x) . Xét các tập hợp:

\(A = \left\{ {x \in \mathbb{R}\mid f\left( x \right) = 0} \right\}\)

\(B = \left\{ {x \in \mathbb{R}\mid g\left( x \right) = 0} \right\}\)

\(C = \left\{ {x \in \mathbb{R}\mid \frac{{f\left( x \right)}}{{g\left( x \right)}} = 0} \right\}\)

Trong các mệnh đề sau, mệnh đề nào đúng?

A. C = A ∪ B.

B. C = A.

C. C = A ∖ B.

D. C = B ∖ A.

Tập xác định của hàm số \(y = \frac{{{\rm{cot}}x}}{{{\rm{sin}}x - 1}}\) là:

A. \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{3} + k2\pi \mid {\rm{k}} \in \mathbb{Z}} \right\}\)

B. \(D = \mathbb{R}\backslash \left\{ {\frac{{{\rm{k}}\pi }}{2}\mid {\rm{k}} \in \mathbb{Z}} \right\}\)

C. \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi ;{\rm{k}}\pi \mid {\rm{k}} \in \mathbb{Z}} \right\}\)

D. \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k2\pi \mid {\rm{k}} \in \mathbb{Z}} \right\}\)

Có bao nhiêu giá trị của tham số m để giá trị lớn nhất của hàm số\[y = \frac{{x - {m^2} - 2}}{{x - m}}\] trên đoạn [0; 4] bằng ‒1?

A. 3.

B. 2.

C. 1.

D. 0.

A. \(\forall M,\overrightarrow {MA} = \overrightarrow {MB} .\)

B. \(\exists M,\overrightarrow {MA} = \overrightarrow {MB} = \overrightarrow {MC} .\)

C. \(\forall M,\overrightarrow {MA} \ne \overrightarrow {MB} \ne \overrightarrow {MC} .\)

D. \(\exists M,\overrightarrow {MA} = \overrightarrow {MB} .\)

Cho hình lăng trụ ABC. A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) trùng với trọng tâm tam giác ABC. Biết khoảng cách giữa hai đường thẳng AA' và BC bằng \[a\sqrt {34} \]. Tính theo a thể tích V của khối lăng trụ ABC. A'B'C'.

A. \(\frac{{{a^3}\sqrt 3 }}{6}.\)

B. \(\frac{{{a^3}\sqrt 3 }}{{12}}.\)

C. \(\frac{{{a^3}\sqrt 3 }}{3}.\)

D. \(\frac{{{a^3}\sqrt 3 }}{{24}}.\)

Có bao nhiêu số nguyên x thỏa mãn (x ‒ 7)(x + 5) < 0 ?

A. 4.

B. 11.

C. 5.

D. Không tồn tại x.

Phương trình \(\sqrt 3 {\rm{sin}}2x - {\rm{cos}}2x + 1 = 0\) có nghiệm là:

A.\(\left[ {\begin{array}{*{20}{l}}{x = k\pi }\\{x = \frac{\pi }{3} + k\pi }\end{array}{\rm{\;}}\left( {k \in \mathbb{Z}} \right)} \right.\)

B. \(\left[ {\begin{array}{*{20}{l}}{x = k\pi }\\{x = \frac{{2\pi }}{3} + k2\pi }\end{array}{\rm{\;}}\left( {k \in \mathbb{Z}} \right)} \right.\)

C. \(\left[ {\begin{array}{*{20}{l}}{x = k2\pi }\\{x = \frac{{2\pi }}{3} + k2\pi }\end{array}{\rm{\;}}\left( {k \in \mathbb{Z}} \right)} \right.\)

D. \(\left[ {\begin{array}{*{20}{l}}{x = k\pi }\\{x = \frac{{2\pi }}{3} + k\pi }\end{array}{\rm{\;}}\left( {k \in \mathbb{Z}} \right)} \right.\)

A. Đồng biến.

B. Nghịch biến.

C. Không đổi.

D. Không kết luận được.

Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipid trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipid. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipid. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 250 nghìn đồng; 1kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Trong các mệnh đề sau, mệnh đề nào không phải định lý?

B. Điều kiện đủ để diện tích tam giác bằng nhau là hai tam giác ấy bằng nhau

C. Điều kiện đủ để hai đường chéo của một tứ giác vuông góc với nhau là tứ giác ấy là hình thoi.

D. Điều kiện đủ để một số nguyên dương a  có tận cùng bằng 5  là số đó chia hết cho 5.

Trong các mệnh đề sau, mệnh đề nào là định lý?

A. ∀x ∈ ℝ, x > −2 ⇒ x² > 4.

B. ∀x ∈ ℝ, x > 2 ⇒ x² > 4.

C. ∀x ∈ ℝ, x² > 4⇒ x > 2.

D. ∀x ∈ ℝ, x² > 4 ⇒ x > −2.

Hàm số y = sinx có tập xác định là:

A. ℝ ∖ {kπ, k ∈ ℤ}

B. \[\mathbb{R} \setminus \left\{ {\frac{{k\pi }}{2},k \in \mathbb{Z}} \right\}\]

C. \[\mathbb{R} \setminus \left\{ {\frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\]

D. ℝ.

Tiếp tuyến tại điểm cực tiểu của đồ thị hàm số  \[y = \frac{1}{3}{x^3} - 2{x^2} + 3x - 5\] là đường thẳng:

A. Song song với đường thẳng x = 1.

B. Song song với trục hoành.

C. Có hệ số góc dương.

D. Có hệ số góc bằng ‒1.

Có bao nhiêu giá trị nguyên của tham số m để hàm số\[y = \sqrt {5 - m\sin x - \left( {m + 1} \right)\cos x} \] xác định trên ℝ?

A. 6

B. 8

C. 7

D. 5

Tam giác ABC có BC = 10 và góc A = 30⁰. Tính bán kính của đường tròn ngoại tiếp tam giác ABC.

A. 4

B. 5

C. 8

D. 10

Cho hình lăng trụ ABC.A'B'C có đáy là tam giác đều cạnh a. Mặt bên BB'C'C' là hình thoi và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa CC' và mặt phẳng (ABB'A) bằng \[\frac{{a\sqrt {12} }}{5}.\] Thể tích khối lăng trụ ABC.A'B'C bằng:

A. \(\frac{{{a^3}}}{6}.\)

B. \(\frac{{{a^3}\sqrt {21} }}{{14}}.\)

C. \(\frac{{3{a^3}}}{8}.\)

D. \(\frac{{{a^3}\sqrt {21} }}{7}.\)

Điều kiện để hàm số bậc ba không có cực trị là phương trình y’ = 0 có:

A. nghiệm kép.

B. vô nghiệm.      

C. hai nghiệm phân biệt.

D. Cả A và B đúng.

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và mặt bên hợp với đáy một góc 60°. Thể tích khối chóp S.ABC là:

A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)

B. \(\frac{{{a^3}\sqrt 2 }}{{24}}\)

C. \(\frac{{{a^3}\sqrt 3 }}{{24}}\)

D. \(\frac{{{a^3}}}{{24}}\)

Cho hình chóp đều S.ABCD có cạnh đáy bằng a và cạnh bên tạo với mặt đáy một góc 60°. Tính thể tích của khối chóp S.ABCD ?

A. \(\frac{{{a^3}\sqrt 3 }}{2}\).

B. \(\frac{{{a^3}\sqrt 6 }}{2}\).

C. \(\frac{{{a^3}\sqrt 3 }}{6}\).

D. \(\frac{{{a^3}\sqrt 6 }}{6}\).

Cho hai đồ thị hàm số y = x³ + 2x² ‒ x + 1 và đồ thị hàm số y = x² ‒ x + 3 có tất cả bao nhiêu điểm chung?

A. 0

B . 3

C. 2

D. 1

Cho hàm số x³ ‒ (2m + 1)x² + (m² ‒3m + 2)x + 4. Tìm m để hàm số có cực đại và cực tiểu nằm về hai phía với trục tung.

Cho hàm số y = −x⁴ + 2(m − 2)x² + 3m. Với giá trị nào của m thì hàm số đã cho có 3 cực trị.

A. m ≤ 2.

B. m > 2.

C. m ≥ 2.

D. m < 2.

Cho hàm số y = f(x) có đồ thị hàm số như hình dưới đây:

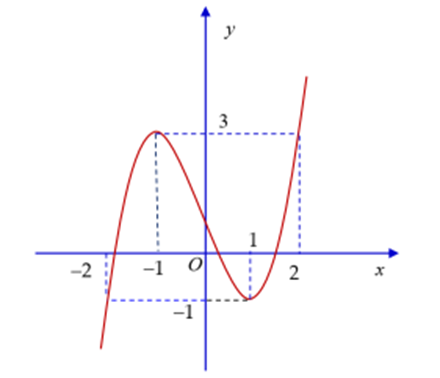
Có tất cả bao nhiêu giá trị nguyên của m để phương trình f(x³ + 3x² − m) − 3= 0 có nghiệm thuộc đoạn [−1;2]?

A. 23

B. 22

C. 19

D. 24

Cho hình vuông ABCD cạnh a. Tính \[\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cdot \left( {\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} } \right).\]

A. \[P = 2\sqrt 2 a.\]

B. P = 2a².

C. P = a².

D. P = ‒2a².

‒9 có thuộc tập hợp ℚ không?

Rút gọn phân số \[\frac{{36}}{{63}}\] ta được phân số tối giản là:

A. \[\frac{3}{4}\]

B. \[\frac{3}{7}\]

C. \[\frac{4}{7}\]

D. \[\frac{5}{9}\]

Cho hai điểm A, B phân biệt. Xác định điểm M biết \[2\overrightarrow {MA} - 3\overrightarrow {MB} = \overrightarrow 0 \]

A. M nằm trên tia AB và AM = 4AB;

B. M nằm trên tia AB và AM = AB;

C. M nằm trên tia AB và AM = 3AB;

D. M nằm trên tia AB và AM = 2AB.

Cho tam giác ABC. Tìm điểm M thỏa mãn \[\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \]

A. M là trung điểm của cạnh IC, với I là trung điểm của AB.

B. M trùng với đỉnh C của ∆ABC.

C. M là trọng tâm của ∆ABC.

D. M là đỉnh của hình bình hành MCAB.

Bác Bình tham gia chương trình bảo hiểm An sinh xã hội của công ty bảo hiểm với thể lệ như sau: Cứ đến tháng 9 hàng năm bác Bình đóng vào công ty 20 triệu đồng với lãi suất hàng năm không đổi \(6{\rm{\% }}/\) năm. Hỏi sau it nhất bao nhiêu năm bác Bình thu về tổng tất cả số tiền lớn hơn 400 triệu đồng?

A. 14 năm.

B. 12 năm.

C. 11 năm.

D. 13 năm.

Cho góc nhọn α thỏa mãn \[\cos \sin \alpha = \frac{1}{3}\,.\] Giá trị của sinα.cosα là:

A. \[\frac{2}{3}\]

B. \[\frac{3}{2}\]

C. \[\frac{4}{9}\]

D. \[\frac{9}{4}\]

Cho hai điểm cố định A; B. gọi I là trung điểm của AB. Tập hợp các điểm M thoả mãn: \[\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} - \overrightarrow {MB} } \right|\]

A. Đường tròn đường kính AB.

B. Trung trực của AB.

C. Đường tròn tâm I, bán kính AB.

D. Nửa đường tròn đường kính AB.

Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn AB. Gọi M là một điểm trên cạnh CD; (α) là mặt phẳng qua M và song song với SA và BC. Thiết diện của mp(α) với hình chóp là:

A. Hình tam giác.

B. Hình thang.

C. Hình bình hành.

D. Hình chữ nhật.

Cho hình vuông ABCD cạnh a. Gọi E là điểm đối xứng của D qua C. Tính \[\overrightarrow {AE} \cdot \overrightarrow {AB} \]

A. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = 2{a^2}.\]

B. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = \sqrt 3 {a^2}.\]

C. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = \sqrt 5 {a^2}.\]

D. \[\overrightarrow {AE} \cdot \overrightarrow {AB} = 5{a^2}.\]

Chọn ngẫu nhiên một số tự nhiên A có bốn chữ số. Gọi N là số thỏa mãn 3^N = A. Xác suất để N là số tự nhiên bằng:

A. \[\frac{1}{{4500}}.\]

B. 0

C. \[\frac{1}{{2500}}.\]

D. \[\frac{1}{{3000}}.\]

Có hai cơ sở khoan giếng A và B. Cơ sở A giá mét khoan đầu tiên là 8000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét sau tăng thêm 500 (đồng) so với giá của mét khoan ngay trước đó. Cơ sở B: Giá của mét khoan đầu tiên là 6000 (đồng) và kể từ mét khoan thứ hai, giá của mỗi mét khoan sau tăng thêm 7% giá của mét khoan ngay trước đó. Một công ty giống cây trồng muốn thuê khoan hai giếng với độ sâu lần lượt là 20 m và 25 m để phục vụ sản xuất. Giả thiết chất lượng và thời gian khoan giếng của hai cơ sở là như nhau. Công ty ấy nên chọn cơ sở nào để tiết kiệm chi phí nhất?

A. Luôn chọn A.

B. Luôn chọn B.

C. Giếng 20m chọn A còn giếng 25m chọn B.

D. Giếng 20 m chọn B còn giếng 25 m chọn A.

Giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{2}{{{x^2} - 5x + 9}}\) bằng

A. \(\frac{{11}}{4}\).

B. \(\frac{4}{{11}}\).

C. \(\frac{{11}}{8}\).

D. \(\frac{8}{{11}}\).

Đồ thị hàm số y = x³ ‒ (3m + 1)x² + (m² + 3m + 2)x + 3 có điểm cực tiểu và điểm cực đại nằm về hai phía của trục tung khi:

A. 1< m < 2.

B. ‒2 < m < ‒1.

C. 2 < m < 3.

D. ‒3 < m < ‒2.

Có bao nhiêu giá trị nguyên của tham số m để hàm số y = −x⁴ + 6x² + mx có ba điểm cực trị?

A. 17

B. 15

C. 3

D. 7

Người ta dự định xây dựng một tòa tháp 11 tầng tại một ngôi chùa nọ theo cấu trúc, diện tích của mặt sàn tầng trên bằng nửa diện tích mặt sàn tầng dưới, biết diện tích mặt đáy tháp là 15 m². Yêu cầu là nền tháp lát gạch hoa kích thước 30x30 (cm). Tính số lượng gạch hoa cần mua để lát sàn tháp.

A. 333 viên gạch

B. 334 viên gạch

C. 332 viên gạch

D. 335 viên gạch

Số tam giác xác định bởi các đỉnh của một đa giác đều 10 cạnh là:

A. 35

B. 120

C. 240

D. 720

Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương, anh A đều phải cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A mua được ô tô giá 500 triệu, biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe?

A.11

B. 12

C. 13

D. 10

A. \[2\sqrt {17} .\]

B. \[12\]

C. \[4\sqrt {13} .\]

D. 9