44 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 36)
Haylamdo biên soạn và sưu tầm 44 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
44 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 36)
Câu 1:
Biết rằng \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x} = 1\). Tìm giá trị thực của tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{1 + \cos x}}{{{{\left( {x - \pi } \right)}^2}}},\,\,\,\,\,\,x \ne \pi \\m,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = \pi \end{array} \right.\) liên tục tại x = π.
A. \(m = \frac{\pi }{2}\).
B. \(m = - \frac{\pi }{2}\).
C. \(m = \frac{1}{2}\).
D. \(m = - \frac{1}{2}\).
Xem lời giải »
Câu 2:
Có bao nhiêu số tự nhiên nhỏ hơn 100 chia hết cho 2 và 3.
Xem lời giải »
Câu 3:
Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có sin2α + cos2α = 1.
Xem lời giải »
Câu 5:
Trong lớp 10C có 16 học sinh giỏi Toán, 15 học sinh giỏi Lí, 11 học sinh giỏi Hóa. Biết rằng có 9 học sinh vừa giỏi Toán và Lí, 6 học sinh vừa giỏi Lí và Hóa, 8 học sinh vừa giỏi Hóa và Toán, trong đó có 11 học sinh giỏi đúng 2 môn. Hỏi có bao nhiêu học sinh trong lớp:
a) Giỏi cả ba môn.
b) Giỏi đúng 1 môn.
Xem lời giải »
Câu 6:
Có bao nhiêu số tự nhiên có 9 chữ số mà các chữ số của nó viết theo thứ tự giảm dần?
A. 5.
B. 15.
C. 55.
D. 10.
Xem lời giải »
Câu 7:
Tập giá trị T của hàm số y = sin2x là
A. T = [–1; 1].
B. T = [0; 1].
C. T = (–1; 1).
D. T = [–2; 2].
Xem lời giải »
Câu 8:
Cho tam giác ABC. Gọi I là điểm trên cạnh BC sao cho 2CI = 3BI và J là điểm trên BC kéo dài sao cho 5JB = 2JC. Gọi G là trọng tâm tam giác.
a) Biểu diễn \(\overrightarrow {AB} ,\overrightarrow {AC} \) theo hai vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \) và biểu diễn \(\overrightarrow {AJ} \) qua \(\overrightarrow {AB} ,\overrightarrow {AC} \).
b) Biểu diễn \(\overrightarrow {AG} \) theo hai vectơ \(\overrightarrow {AI} ,\overrightarrow {AJ} \).
Xem lời giải »
Câu 9:
Cho tam giác ABC có AB = 2, AC = 3, \[\widehat {BAC} = 60^\circ \]. Gọi M là trung điểm của đoạn thẳng BC. Điểm D thỏa mãn \(\overrightarrow {AD} = \frac{7}{{12}}\overrightarrow {AC} \).
a) Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
b) Biểu diễn \(\overrightarrow {AM} ,\,\overrightarrow {BD} \) theo \(\overrightarrow {AB} ,\overrightarrow {AC} \).
c) Chứng minh AM ⊥ BD.
Xem lời giải »
Câu 10:
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
A. 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II.
B. 10 tấn nguyên liệu loại I và 2 tấn nguyên liệu loại II.
C. 10 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.
D. 4 tấn nguyên liệu loại I và 5 tấn nguyên liệu loại II.
Xem lời giải »
Câu 11:
Giải phương trình sin2x – cos2x + 3sinx – cosx – 1 = 0.
Xem lời giải »
Câu 12:
Cho A = (2m – 1; m + 3) và B = (–4; 5). Tìm m sao cho:
a) A là tập hợp con của B.
b) B là tập con của A.
c) A ∩ B = ∅.
d) A ∪ B là một khoảng.
Xem lời giải »
Câu 14:
Cho tam giác ABC, lấy các điểm M, N, P sao cho \(\overrightarrow {MB} = 3\overrightarrow {MC} \); \(\overrightarrow {NA} + 3\overrightarrow {NC} = \vec 0\) và \(\overrightarrow {PA} + \overrightarrow {PB} = \vec 0\).
a) Tính \(\overrightarrow {PM} ,\,\,\overrightarrow {PN} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Chứng minh rằng: M, N, P thẳng hàng.
Xem lời giải »
Câu 15:
Cho tam giác ABC, lấy các điểm M, N, P thỏa mãn \(\overrightarrow {MA} + \overrightarrow {MB} = \vec 0\); \(3\overrightarrow {AN} - 2\overrightarrow {AC} = \vec 0\); \(\overrightarrow {PB} = 2\overrightarrow {PC} \). Ba điểm nào sau đây thẳng hàng?
A. M, N, P;
B. A, M, B;
C. A, N, C;
D. M, N, B.
Xem lời giải »
Câu 16:
Bác Năm dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích 8 ha. Nếu trồng 1 ha ngô thì cần 20 ngày công và thu được 40 triệu đồng. Nếu trồng 1 ha đậu xanh thì cần 30 ngày công và thu được 50 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng không quá 180 ngày công cho việc trồng ngô và đậu xanh.
Xem lời giải »
Câu 17:
Lớp 10B có 45 học sinh. Trong kì thi học kì I có 20 em đạt loại giỏi môn Toán; 18 em đạt loại giỏi môn Tiếng Anh; 17 em đạt loại giỏi môn Ngữ văn; 5 em đạt loại giỏi cả ba môn học trên và 7 em không đạt loại giỏi môn nào trong ba môn học trên. Số học sinh chỉ đạt loại giỏi một trong ba môn học trên là:
A. 40.
B. 26.
C. 21.
D. 17.
Xem lời giải »
Câu 18:
Trong lớp 10B có 45 học sinh, 25 học sinh thích môn Văn, 20 học sinh thích môn Toán, 18 học sinh thích môn Sử, 6 học sinh không thích môn nào, 5 học sinh thích cả 3 môn. Hỏi số học sinh chỉ thích một trong 3 môn trên?
Xem lời giải »
Câu 19:
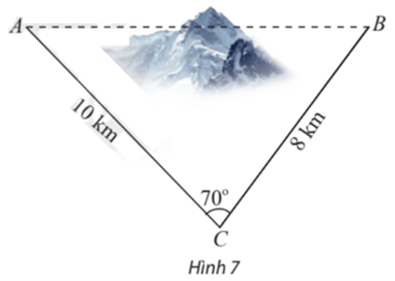
Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8 km. Góc tạo bởi hai đoạn dây AC và CB là 70°. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
Xem lời giải »
Câu 20:
Cho tứ diện đều ABCD, cạnh a. Gọi I, J lần lượt là trung điểm của AC, BC. Gọi K là một điểm trên cạnh BD sao cho KB = 2KD.
a) Xác định thiết diện của tứ diện với mặt phẳng (IJK). Chứng minh thiết diện là hình thang cân.
b) Tính diện tích thiết diện đó.
Xem lời giải »
Câu 21:
Phương là gì, chiều là gì, hướng là gì trong toán học?
Xem lời giải »
Câu 22:
Có 30 tấm thẻ đánh số từ 1 đến 30. Lấy ngẫu nhiên 3 tấm thẻ rồi nhân các số trên 3 thẻ. Tìm xác suất để kết quả đạt được là một số chia hết cho 6.
A. \(\frac{{115}}{{406}}\).
B. \(\frac{{512}}{{812}}\).
C. \(\frac{{517}}{{812}}\).
D. \(\frac{{495}}{{812}}\).
Xem lời giải »
Câu 23:
Cho tam giác ABC đều cạnh a. Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\) bằng:
A. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \).
B. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \frac{{a\sqrt 3 }}{2}\).
C. \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a\).
D. Một đáp án khác.
Xem lời giải »
Câu 24:
Cho tam giác ABC đều cạnh a. Tính độ dài các vectơ \(\overrightarrow {AB} - \overrightarrow {AC} ;\overrightarrow {AB} + \overrightarrow {AC} \).
Xem lời giải »
Câu 25:
Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng (SAB) bằng \(\frac{{a\sqrt 3 }}{3}\) và \(\widehat {SAO} = 30^\circ ,\,\,\widehat {SAB} = 60^\circ \). Độ dài đường sinh của hình nón theo a bằng
A. \(a\sqrt 2 \).
B. \(a\sqrt 3 \).
C. \(2a\sqrt 3 \).
D. \(a\sqrt 5 \).
Xem lời giải »
Câu 27:
Viết số thích hợp vào chỗ chấm: \(\frac{1}{5}\) tấn = ... kg.
Xem lời giải »
Câu 28:
Cho nửa đường tròn (O; R) đường kính AB, vẽ hai tiếp tuyến Ax, By với nửa đường tròn. Trên tia Ax lấy điểm E (E khác A, AE < R), trên nửa đường tròn lấy điểm M sao cho EM = EA, đường thẳng EM cắt tia By tại F.
a) Chứng minh EF là tiếp tuyến của đường tròn (O).
b) Chứng minh tam giác EOF là tam giác vuông.
c) Chứng minh AM.OE + BM.OF = AB.EF.
d) Tìm vị trí điểm E trên tia Ax sao cho \({S_{\Delta AMB}} = \frac{3}{4}{S_{\Delta EOF}}\).
Xem lời giải »
Câu 29:
Lấy một điểm M tùy ý. Chứng minh rằng: G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
Xem lời giải »
Câu 30:
Ba bạn Hồng, Hoa, Lan có tất cả 134 cái bưu ảnh. Biết rằng số bưu ảnh của Hoa nhiều hơn Hồng 14 chiếc song lại kém Lan 16 chiếc. Tính số bưu ảnh của mỗi bạn.
Xem lời giải »
Câu 32:
Tìm \(\overline {abcd} \), biết \(\overline {abc} = 5 \times \overline {dad} \).
Xem lời giải »
Câu 33:
Chọn ngẫu nhiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để số được chọn có tổng các chữ số là chẵn bằng:
A. \(\frac{{41}}{{81}}\).
B. \(\frac{4}{9}\).
C. \(\frac{1}{2}\).
D. \(\frac{{16}}{{81}}\).
Xem lời giải »
Câu 34:
Tính bằng cách thuận tiện: (–525) – [(475 + 245) – 45].
Xem lời giải »
Câu 35:
Họ nguyên hàm của hàm số \(f\left( x \right) = \frac{{\ln x}}{x}\) là:
A. ln2x + C.
B. lnx + C.
C. \(\frac{{{{\ln }^2}x}}{2} + C\).
D. \(\frac{{\ln x}}{2} + C\).
Xem lời giải »
Câu 36:
Ông và bà An cùng có 6 đứa con đang lên máy bay theo một hàng dọc. Có bao nhiêu cách xếp hàng khác nhau nếu ông hay bà An đứng ở đầu hoặc cuối hàng.
A. 720;
B. 1440;
C. 18 720;
D. 40 320.
Xem lời giải »
Câu 37:
Cho đường tròn (O; R) có đường kính BC. Lấy A thuộc (O) sao cho AB < AC, vẽ đường cao AH của tam giác ABC.
a) Chứng minh: AH.BC = AB.AC.
b) Tiếp tuyến tại A của (O) cắt đường thẳng BC tại M. Chứng minh rằng: MA2 = MB.MC.
c) Kẻ HE vuông góc với AB (E thuộc AB) và HF vuông góc với AC (F thuộc AC). Chứng minh AM // EF.
Xem lời giải »
Câu 38:
Một tấm vải dài 36m. Lần đầu người ta cắt ra 16 mảnh vải, mỗi mảnh vải dài \(1\frac{1}{5}\) m. Lần thứ hai người ta cắt được 6 mảnh vải dài như nhau thì vừa hết tấm vải. Hỏi mỗi mảnh vải cắt ra ở lần thứ hai dài bao nhiêu mét?
Xem lời giải »
Câu 39:
Cho hai đường tròn (O) và (O’) tiếp xúc trong tại A. Qua A vẽ dây AB, AC của đường tròn (O), chúng cắt (O’) theo thứ tự tại D và E. Chứng minh BC // DE.
Xem lời giải »
Câu 41:
Trước nửa đêm là bao nhiêu phút nếu trước đó 32 phút thời gian này gấp 3 lần số phút sau 22 giờ?
Xem lời giải »
Câu 42:
Một cửa hàng bán trái cây nhập khẩu 500 kg cam với giá 40 000 đồng/kg. Phí vận chuyển của chuyến hàng là 4 000 000 đồng. Giả sử rằng 10% số kg cam trên bị hư trong quá trình vận chuyển và số kg cam còn lại được bán hết. Hỏi giá bán của mỗi kg cam là bao nhiêu để công ty có lợi nhuận 20% so với tiền vốn ban đầu?
Xem lời giải »
Câu 43:
Cho tam giác ABC vuông tại A, có AH là đường cao, AM là đường trung tuyến. Qua B kẻ đường thẳng vuông góc với AM tại I cắt AC tại E.
a) Chứng minh BI.BE = 2BH.BM.
b) Chứng minh \(\frac{1}{{A{B^2}}} = \frac{1}{{B{E^2}}} + \frac{1}{{B{C^2}}}\).
Xem lời giải »
Câu 44:
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = x2 – 2(m + 1)x – 3 đồng biến trên khoảng (4; 2018)?
Xem lời giải »