91 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 55)
Haylamdo biên soạn và sưu tầm 91 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
91 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 55)
Câu 1:
Cho a, b, c là các số thực dương thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức \(P = \frac{1}{{a + 2b + 3}} + \frac{1}{{b + 2c + 3}} + \frac{1}{{c + 2a + 3}}\).
Câu 2:
Cho các số thực dương thỏa mãn a + b + c = 1. Tìm giá trị lớn nhất của biểu thức: \(P = \frac{a}{{\sqrt {a + bc} }} + \frac{b}{{\sqrt {b + ca} }} + \frac{c}{{\sqrt {c + ab} }}\).
Câu 3:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích của khối lăng trụ đã cho.
Câu 4:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy và cạnh bên cùng bằng a. Tính thể tích của khối lăng trụ đó.
Câu 5:
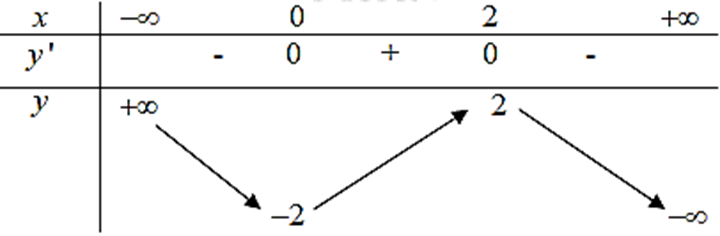
Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số f(x) = |e2x − 4ex + m| trên đoạn [0; ln 4] bằng 6?
Câu 6:
Tìm nguyên hàm F (x) của hàm số f (x) = 6x + sin 3x, biết \(F\left( 0 \right) = \frac{2}{3}\).
Câu 7:
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; −7); B(2; −8). Tính y (−1).
Câu 8:
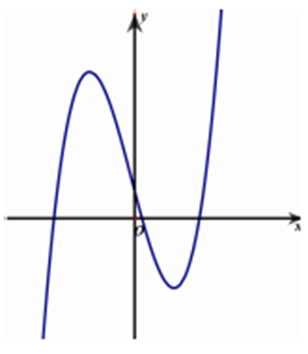
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ) có đồ thị như hình vẽ bên. Tìm số điểm cực trị của hàm số đã cho.
Câu 9:
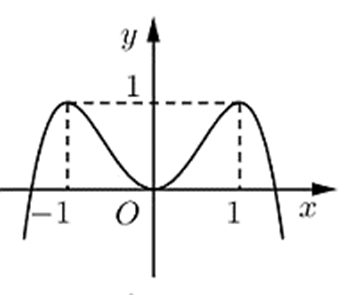
Cho hàm số f (x) = ax4 + bx2 + c (a, b, c Î ℝ). Đồ thị của hàm số y = f (x) như hình vẽ bên. Số nghiệm thực của phương trình 4f (x) − 3 = 0 là:
Câu 10:
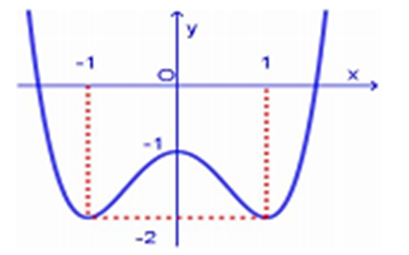
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị như hình vẽ dưới đây. Hỏi phương trình 2f (x) = −1 có bao nhiêu nghiệm?
Câu 11:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Tính khoảng cách từ C đến mặt phẳng (SBD).
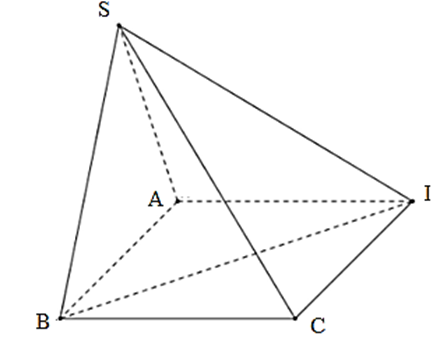
Câu 12:
Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ A đến (SCD).
Câu 13:
Cho x, y là hai số không âm thỏa mãn x + y = 2. Giá trị nhỏ nhất của biểu thức \(P = \frac{1}{3}{x^3} + {x^2} + {y^2} - x + 1\).
Câu 14:
Cho x, y là các số thực không âm thỏa mãn: x2 − 2xy + x − 2y ≤ 0. Tìm GTLN của M = x2 − 5y2 + 3x.
Câu 18:
Với giá trị nào của m thì ba đường thẳng d1: y = x; d2: y = 4 − 3x và d3: y = mx − 3 đồng quy?
Câu 19:
Tam giác đều cạnh a nội tiếp trong đường tròn bán kính R. Khi đó bán kính R bằng bao nhiêu?
Câu 20:
Giải phương trình: \(\tan x - 3\cot x = 4\left( {\sin x + \sqrt 3 \cos x} \right)\).
Câu 23:
Tìm hệ số của số hạng chứa x10 trong khai triển của biểu thức \({\left( {3{x^3} - \frac{2}{{{x^2}}}} \right)^5}\)
Câu 24:
Tìm hệ số của số hạng chứa x10 trong khai triển \(f\left( x \right) = {\left( {\frac{1}{4}{x^2} + x + 1} \right)^2}{\left( {x + 2} \right)^{3n}}\) với n là số tự nhiên thỏa mãn hệ thức \(A_n^3 + C_n^{n - 2} = 14n\)
Câu 25:
Tìm tất cả các giá trị thực của tham số m sao cho hàm số \(y = \frac{{m{x^3}}}{3} + 7m{x^2} + 14x - m + 2\) nghịch biến trên [1; +∞).
Câu 26:
Có bao nhiêu giá trị nguyên của tham số m để hàm số \(y = \sqrt {5 - m\sin x - \left( {m + 1} \right)\cos x} \) xác định trên ℝ?
Câu 27:
Gọi x0 là nghiệm dương của phương trình \({4^{{x^2} - 2x}} = {\left( {\sqrt 2 } \right)^{x + 1}}\). Mệnh đề nào dưới đây đúng?
A. x0 Î (1; 2);
B. x0 Î (0; 1);
C. \({x_0} \in \left( {2;\;\frac{5}{2}} \right)\);
D. \({x_0} \in \left( {0;\;\frac{2}{5}} \right)\).
Câu 28:
Tính tổng các nghiệm thuộc khoảng \(\left( { - \frac{\pi }{2};\;\frac{\pi }{2}} \right)\) của phương trình
4sin2 2x − 1 = 0.
Câu 29:
Giải phương trình sau: \({7^x}\,.\,{27^{\left( {1\, - \,\frac{1}{x}} \right)}} = 3087\).
Câu 31:
Với giá trị lớn nhất của a bằng bao nhiêu để phương trình asin2 x + 2sin 2x + 3acos2 x = 2 có nghiệm?
Câu 32:
Cho hàm số f (x) đồng biến trên khoảng (a; b). Mệnh đề nào sau đây sai?
A. Hàm số y = f (x + 1) đồng biến trên khoảng (a; b);
B. Hàm số y = −f (x) + 1 nghịch biến trên khoảng (a; b);
C. Hàm số y = f (x) + 1 đồng biến trên khoảng (a; b);
D. Hàm số y = −f (x) − 1 nghịch biến trên khoảng (a; b).
Câu 33:
Cho hàm số y = f (x) có đạo hàm trên khoảng (a; b). Mệnh đề nào sau đây sai?
A Nếu f ¢(x) > 0, "x Î (a; b) thì hàm số y = f (x) đồng biến trên (a; b);
B. Nếu f ¢(x) = 0, "x Î (a; b) thì hàm số y = f (x) không đổi trên (a; b);
C. Nếu hàm số y = f (x) nghịch biến trên (a; b) thì f ¢(x) ≤ 0 với mọi x Î (a; b);
D. Nếu hàm số y = f (x) đồng biến trên (a; b) thì f ¢(x) > 0 với mọi x Î (a; b);
Câu 34:
Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của SA, SB, SC, SD. Tính tỉ số thể tích của khối chóp S.MNPQ và khối chóp S.ABCD.
Câu 35:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, M và N theo thứ tự là trung điểm của SA và SB. Tính tỉ số thể tích \(\frac{{{V_{S.CDMN}}}}{{{V_{S.CDAB}}}}\).
Câu 36:
Cho tứ diện ABCD có thể tích bằng V, hai điểm M và P lần lượt là trung điểm AB, CD điểm N thuộc AD sao cho AD = 3AN. Tính thể tích tứ diện BMNP.
Câu 37:
Cho tứ diện ABCD có M, N lần lượt là trung điểm của AB, CD và P là một điểm thuộc cạnh BC (P không trùng trung điểm cạnh BC). Tìm thiết diện của tứ diện cắt bởi mặt phẳng (MNP).
Câu 38:
Câu 39:
Có bao nhiêu giá trị m nguyên thuộc khoảng (−10; 10) để đồ thị hàm số \(y = \frac{{\sqrt {x\left( {x - m} \right)} - 1}}{{x + 2}}\) có đúng ba đường tiệm cận?
Câu 40:
Từ các chữ số 1, 2, 3 có thể lập được bao nhiêu số khác nhau có những chữ số khác nhau.
Câu 41:
Từ các chữ số: 1; 2; 3; 4; 5; 6. Có thể lập được bao nhiêu số có ba chữ số khác nhau và tổng của ba số đó chia hết cho 3.
Câu 42:
Ông A dự định sử dụng hết 5m2 kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Câu 43:
Cho phương trình 3x + m = log3 (x − m) với m là tham số. Có bao nhiêu giá trị nguyên của mÎ (−15; 15) để phương trình đã cho có nghiệm?
Câu 44:
Phương trình log (x2 + mx) = log (x + m − 1) có nghiệm duy nhất khi giá trị của m là bao nhiêu?
Câu 45:
Gọi x0 là nghiệm dương nhỏ nhất của phương trình 3sin2 x + 2sin xcos x − cos2 x = 0. Chọn khẳng định đúng.
A. \({x_0} \in \left( {\frac{\pi }{2};\;\pi } \right)\);
B. \({x_0} \in \left( {\frac{{3\pi }}{2};\;2\pi } \right)\);
C. \({x_0} \in \left( {0;\;\frac{\pi }{2}} \right)\);
D. \({x_0} \in \left( {\pi ;\;\frac{{3\pi }}{2}} \right)\).
Câu 46:
Cho x thỏa mãn \(2\sin 2x - 3\sqrt 6 \left| {\sin x + \cos x} \right| + 8 = 0\). Tính sin 2x.
Câu 47:
Phương trình \(2\sin 2x - 3\sqrt 6 \left| {\sin x + \cos x} \right| + 8 = 0\) có nghiệm là:
Câu 48:
Cho hàm số y = −x3 + 3x2 + 9x − 2 đạt cực trị tại x1, x2. Tính giá trị của biểu thức S = x12 + x22.
Câu 49:
Cho hàm số y = −x3 + 3x2 + 6x. Hàm số đạt cực trị tại hai điểm x1, x2. Khi đó giá trị của biểu thức S = x12 + x22 bằng:
Câu 50:
Cho hàm số y = (m − 1)x3 + (m − 1)x2 − 2x + 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)?
Câu 51:
Tìm tất cả các giá trị của m để hàm số y = (m − 1)x3 − 3(m − 1)x2 + 3x + 2 đồng biến biến trên ℝ.
Câu 52:
Có bao nhiêu cách sắp xếp 8 viên bi đỏ khác nhau và 8 viên bi đen khác nhau thành một dãy sao cho hai viên bi cùng màu không được ở cạnh nhau?
Câu 54:
Có bao nhiêu số tự nhiên có 2 chữ số, điều kiện là hai số này phải khác nhau hoàn toàn?
Câu 55:
Khẳng định nào sau đây là đúng?
A. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) thì hàm số f (x) + g (x) đồng biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) và đều nhận giá trị dương trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
C. Nếu các hàm số f (x), g (x) đồng biến trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
D. Nếu các hàm số f (x), g(x) nghịch biến trên (a; b) và đều nhận giá trị âm trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b).
Câu 56:
Khẳng định nào sau đây là đúng?
A. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) thì hàm số f (x) + g (x) đồng biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) và đều nhận giá trị dương trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
C. Nếu các hàm số f (x), g (x) đồng biến trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
D. Nếu các hàm số f (x), g(x) nghịch biến trên (a; b) và đều nhận giá trị âm trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b).
Câu 57:
A. Hàm số y = f (x) đạt cực trị tại x0 thì f ¢(x0) = 0;
B. Nếu hàm số đạt cực trị tại x0 thì hàm số không có đạo hàm tại x0 hoặc f ¢(x0) = 0;
C. Hàm số y = f (x) đạt cực trị tại x0 thì nó không có đạo hàm tại x0;
D. Hàm số y = f (x) đạt cực trị tại x0 thì f ¢¢(x0) > 0 hoặc f ¢¢(x0) < 0.
Câu 58:
A. Nếu hàm số f (x) đồng biến trên (a; b) thì hàm số −f (x) nghịch biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b) thì hàm số \(\frac{1}{{f\left( x \right)}}\) nghịch biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b) thì hàm số \(\frac{1}{{f\left( x \right)}}\) nghịch biến trên (a; b);
D. Nếu hàm số f (x) đồng biến trên (a; b) thì hàm số −f (x) − 2016 nghịch biến trên (a; b).
Câu 59:
A. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) thì hàm số f (x) + g (x) đồng biến trên (a; b);
B. Nếu hàm số f (x) đồng biến trên (a; b), hàm số g (x) nghịch biến trên (a; b) và đều nhận giá trị dương trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
C. Nếu các hàm số f (x), g (x) đồng biến trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b);
D. Nếu các hàm số f (x), g(x) nghịch biến trên (a; b) và đều nhận giá trị âm trên (a; b) thì hàm số f (x).g (x) đồng biến trên (a; b).
Câu 61:
Nếu hàm số y = f (x) đồng biến trên khoảng (0; 2) thì hàm số y = f (2x) đồng biến trên khoảng nào?
Câu 63:
A. 4t2 – t – 1 = 0.
B. 2t2 – t – 1 = 0.
C. 2t2 – t – 2 = 0.
C. 2t2 – t – 2 = 0.
Câu 66:
Cho hàm số y = f (x) có đạo hàm f ¢(x) = (x − 1)(x2 − 2)(x4 − 4). Tìm số điểm cực trị của hàm số y = f (x).
Câu 67:
Cho hàm số y = f (x) có đạo hàm f ¢(x) = (x + 1)2(x − 2)3(2x + 3), "x Î ℝ. Tìm số điểm cực trị của hàm số đã cho.
Câu 68:
Cho phương trình \(3\sqrt 2 \left( {\sin x + \cos x} \right) + 2\sin 2x + 4 = 0\). Đặt t = sin x + cos x, ta được phương trình nào dưới đây?
A. \(2{t^2} + 3\sqrt 2 t + 2 = 0\);
B. \(4{t^2} + 3\sqrt 2 t + 4 = 0\);
C. \(2{t^2} + 3\sqrt 2 t - 2 = 0\);
D. \(4{t^2} + 3\sqrt 2 t - 4 = 0\).
Câu 70:
Ông A dự định sử dụng hết 5m2 kính để làm bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có thể tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Câu 71:
Người ta làm một cái hộp không có nắp bằng bìa cứng dạng hình lập phương có cạnh 2,5 dm. Tính diện tích bìa cần dùng để làm hộp không tính mép dán.
Câu 72:
Cho khối trụ có chiều cao h = 8, bán kính đường tròn đáy bằng 6, cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 4. Tính diện tích thiết diện tạo thành.
Câu 73:
Cho khối trụ có hai đáy là (O) và (O'). AB, CD lần lượt là hai đường kính của (O) và (O'), góc giữa AB và CD bằng 30°, AB = 6 và thể tích khối tứ diện ABCD bằng 30. Thể tích khối trụ đã cho bằng:
Câu 74:
Tìm m để phương trình cos 2x − (2m − 1)cos x − 2m = 0 có nghiệm \(x \in \left( { - \frac{\pi }{2};\;\frac{\pi }{2}} \right)\).
Câu 75:
Tìm tất cả giá trị thực của tham số m để phương trình cos 2x − (2m + 1)cos x + m + 1 = 0 có nghiệm trên khoảng \(\left( {\frac{\pi }{2};\;\frac{{3\pi }}{2}} \right)\).
Câu 76:
Câu 78:
Cho a, b, c là các số thực dương thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức \(P = \frac{1}{{a + 2b + 3}} + \frac{1}{{b + 2c + 3}} + \frac{1}{{c + 2a + 3}}\).
Câu 79:
Cho các số thực dương thỏa mãn a + b + c = 1. Tìm giá trị lớn nhất của biểu thức: \(P = \frac{a}{{\sqrt {a + bc} }} + \frac{b}{{\sqrt {b + ca} }} + \frac{c}{{\sqrt {c + ab} }}\).
Câu 80:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích của khối lăng trụ đã cho.
Câu 81:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy và cạnh bên cùng bằng a. Tính thể tích của khối lăng trụ đó.
Câu 82:
Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số f (x) =
|e2x − 4ex + m| trên đoạn [0; ln 4] bằng 6?
Câu 83:
A. f (x) = 3x − 4e2x + 10;
B. f (x) = 3x − 4e2x + 14;
C. f (x) = 3x − 2e2x + 12;
D. f (x) = 3x − 2 e2x + 10.
Câu 84:
Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị là A(1; −7); B(2; −8). Tính y (−1).
Câu 85:
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d Î ℝ) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:
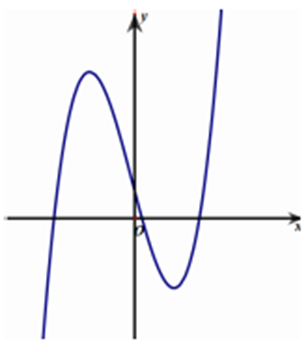
Câu 86:
Cho hàm số f (x) = ax4 + bx2 + c (a, b, c Î ℝ). Đồ thị của hàm số y = f (x) như hình vẽ bên. Số nghiệm thực của phương trình 4f (x) − 3 = 0 là:
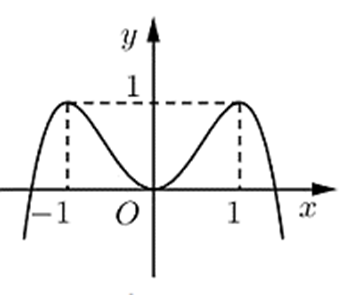
Câu 87:
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị như hình vẽ dưới đây. Hỏi phương trình 2f (x) = −1 có bao nhiêu nghiệm?
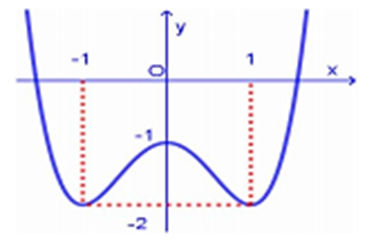
Câu 88:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ C đến mặt phẳng (SBD) bằng
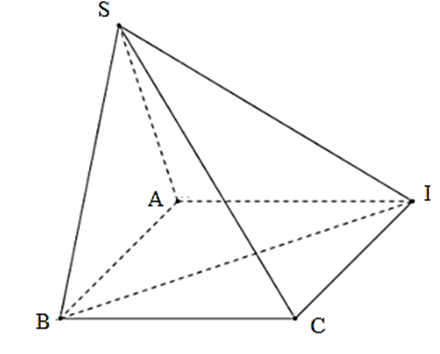
Câu 89:
Cho hình chóp S ABCD, có đáy ABCD là hình vuông cạnh bằng 1. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy (ABCD). Tính khoảng cách từ A đến (SCD).
Câu 90:
Cho x, y là hai số không âm thỏa mãn x + y = 2. Giá trị nhỏ nhất của biểu thức \(P = \frac{1}{3}{x^3} + {x^2} + {y^2} - x + 1\)
Câu 91:
Cho x, y là các số thực không âm thỏa mãn: x2 − 2xy + x − 2y ≤ 0.
Tìm GTLN của M = x2 − 5y2 + 3x.