174 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 44)
Haylamdo biên soạn và sưu tầm 174 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
174 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 44)
Câu 1:
Cho A, B, C nằm trên đường thẳng xy theo thứ tự đó. Vẽ đường tròn (O) đi qua B và C. Từ điểm A, vẽ hai tiếp tuyến AM; AN. Gọi E và F lần lượt là trung điểm của BC và MN.
a) Chứng minh AM2 = AN2 = AB.AC.
b) ME cắt (O) tại I. Chứng minh IN // AB.
c) Chứng minh tâm đường tròn ngoại tiếp tam giác OEF nằm trên 1 đường thẳng cố định khi (O) thay đổi nhưng luôn đi qua B và C.
Câu 3:
Bạn An nghĩ ra một số có 3 chữ số biết rằng số đó chia hết cho 18 và các chữ số của nó tỉ lệ với 1, 2, 3 và chữ số tận cùng là số chẵn.
Câu 5:
Cho hai tập hợp A = [m – 4; 1], B = (–3; m]. Tính tổng tất cả các giá trị nguyên của m để A ∪ B = B.
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD, AB = 2CD). M là 1 điểm nằm trên SC sao cho MS = MC.
a) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Xác định giao điểm K của AM với (SBD), tính \(\frac{{AK}}{{AM}}\).
Câu 7:
Cho hình chữ nhật ABCD có AB bằng 6 cm BC = 4 cm quay hình chữ nhật đó quanh AB. Diện tích xung quanh và diện tích toàn phần của hình trụ là S1, S2. Tính S1, S2?
Câu 8:
Hình thang vuông ABCD có \(\widehat A = \widehat D = 90^\circ \), AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.
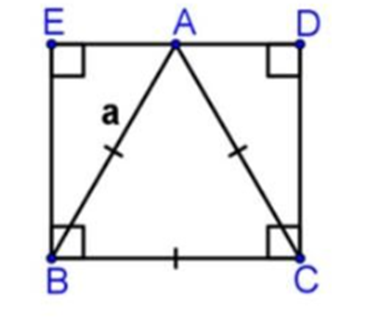
Câu 9:
cho tam giác ABC cân tại A. Vẽ đường tròn tâm O, đường kính BC. Đường tròn (O) cắt AB và AC lần lượt tại M và N.
a) Chứng minh các cung nhỏ BM và CN có số đo bằng nhau.
b) Tính \(\widehat {MON}\) biết \(\widehat {BAC} = 40^\circ \).
Câu 10:
Cho tam giác ABC có BC = 3cm và đường cao AH = 4 cm, khi đó diện tích tam giác ABC là?
Câu 11:
Cho tam giác ABC Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm của DF và BC. Chứng minh \(\frac{{DM}}{{MF}} = \frac{{AC}}{{AB}}\).
Câu 12:
Có bao nhiêu số tự nhiên có 5 chữ số dạng \(\overline {abcde} \) thỏa mãn a ≤ b ≤ c ≤ d ≤ e?
Câu 13:
Cho ∆ABC vuông tại A (AB < AC). Kẻ BD là phân giác của \(\widehat {ABD}\) (D thuộc AC), trên cạnh BC lấy điểm E sao cho AB = BE.
a) Chứng minh ∆ABD = ∆EBD.
b) So sánh AD và DC.
c) Đường thẳng ED cắt đường thẳng AB tại F, gọi S là trung điểm của FC. Chứng minh ba điểm B, D, S thẳng hàng.
Câu 14:
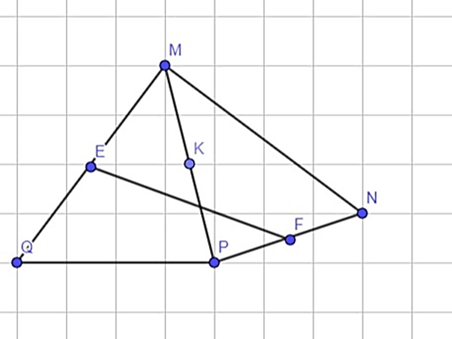
Cho tứ giác MNPQ ( hình bên ) . Ba điểm E, F, K lần lượt là trung điểm của MQ, NP và MP. Kết luận nào sau đây đúng?
A. \(EF = \frac{{MN + PQ}}{2}\).
B. \(EF \le \frac{{MN + PQ}}{2}\).
C. \(EF < \frac{{MN + PQ}}{2}\).
D. \(\frac{{MN + PQ}}{2} > 2\).
Câu 15:
Hai đội công nhân giao thông cùng sửa 1 đoạn đường. Nếu đội 1 làm nửa quãng đường đó rồi để đội 2 làm tiếp cho đến lúc xong thì thời gian tổng cộng là 8 giờ. Nếu cả 2 cũng làm chung thì đoạn đường được sửa xong trong 3 giờ. Hỏi mỗi đội làm 1 mình thì hết bao nhiêu thời gian để sửa xong quãng đường, biết rằng năng suất lao động của mỗi đội là như nhau.
Câu 16:
Cho \(\left| {x - 2} \right| + \left| {y - 1} \right| + {\left( {x + y - z - 2} \right)^{2022}} = 0\). Tính giá trị biểu thức
A = 5x2y2020z2021.
Câu 17:
Một đàn gà có 16 con gà trống và 34 con gà mái. Tỉ số phần trăm của số gà trống và số gà của đàn?
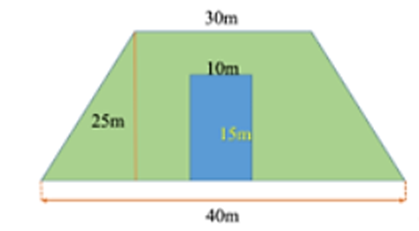
Câu 18:
Nếu một túi hạt giống cỏ gieo vừa đủ trên 25m2 đất, thì cần bao nhiêu túi hạt giống để gieo hết bãi cỏ?
Câu 19:
Rút gọn biểu thức P = \(\frac{{x + 2}}{{x\sqrt x - 1}} + \frac{{\sqrt x + 1}}{{x + \sqrt x + 1}} - \frac{1}{{\sqrt x + 1}}\), với x ≥ 0; x ≠ 1.
Câu 20:
Giải phương trình:
\(\frac{{x - 10}}{{1994}} + \frac{{x - 8}}{{1996}} + \frac{{x - 6}}{{1998}} + \frac{{x - 4}}{{2000}} + \frac{{x - 2}}{{2002}} = \frac{{x - 2002}}{2} + \frac{{x - 2000}}{4} + \frac{{x - 1998}}{6} + \frac{{x - 1996}}{8} + \frac{{x - 1994}}{{10}}\)
Câu 22:
Cho hình thang vuông ABCD, biết \(\widehat A = \widehat D = 90^\circ \), lấy điểm M thuộc cạnh DC, ∆BMC là tam giác đều. Số đo \(\widehat {ABC}\) là:
Câu 23:
Cho hình vuông ABCD. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính SMNPQ theo SABCD?
Câu 24:
Cho tam giác ABC vuông tại A(AB < AC), gọi O là trung điểm của đoạn thẳng BC. Trên tia đối của tia OA lấy điểm K sao cho OA = OK. Vẽ AH vuông góc BC tại H, trên tia HC lấy HD = HA. Đường thẳng vuông góc với BC tại D cắt AC tại E.
a) Chứng minh tam giác ABC bằng tam giác CKA.
b) Chứng minh AB = AE.
c) Gọi M là trung điểm của đoạn thẳng BE. Tính số đo góc CHM.
d) Chứng minh: \[\frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{A{H^2}}}\].
Câu 26:
Có 4 cặp vợ chồng được xếp ngồi trên 1 chiếc ghế dài có 8 chỗ. Biết rằng mỗi người vợ chỉ ngồi cạnh chồng mình hoặc ngồi cạnh 1 người phụ nữ khác. Hỏi có bao nhiêu cách sắp xếp chỗ ngồi thỏa mãn?
Câu 27:
Giá hoa tháng năm tăng 10 % so với giá hoa tháng bốn. Giá hoa tháng sáu tăng 10 % so với giá hoa tháng năm hỏi giá hoa tháng sáu tăng bao nhiêu phần trăm so với sáu tháng bốn?
Câu 30:
Cho hàm số y = \(\frac{{3x - 5m + 6}}{{x + m - 1}}\). Tìm tất cả các giá trị của m để hàm số xác định trên (0; +∞).
Câu 31:
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến tại A của (O), lấy điểm C. Gọi E là giao điểm của CB với (O). từ O kẻ đường thẳng song song với AE cắt BC tại M.
a) Chứng minh CA2 = CE. CB
b) Chứng minh bốn điểm A; C; O; M cùng thuộc 1 đường tròn
Câu 32:
Cho tam giác ABC với trọng tâm G. Chứng minh rằng với điểm M bất kì ta có
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \).
Câu 33:
Cho tứ giác ABCD có 2 góc đối bù nhau. Gọi O là giao điểm 2 đường chéo AC và BD. E là giao điểm 2 đường thẳng AD và BC. Chứng minh AE.CD = CE.AB và\(\widehat {ABD}\)= \(\widehat {DCA}\).
Câu 34:
Một hình thang có đáy nhỏ dài 7cm, đáy lớn dài 17cm được chia thành hai hình thang có đáy chung dài 13cm. Hãy so sánh diện tích hai hình thang có đáy chung nói trên.
Câu 35:
Có 10 người ngồi xung quanh bàn tròn, mỗi người cầm một đồng xu như nhau. Tất cả 10 người cùng tung đồng xu của họ, người có đồng xu ngửa thì đứng, người có đồng xu úp thì ngồi. Tính xác suất để có đúng 4 người cùng đứng ,trong đó có đúng hai người đứng liền kề?
Câu 36:
Một nhà sản xuất quyết định giảm giá 8% cho một dòng máy tính bảng hỏi giá của máy tính bảng sau khi giảm giá là bao nhiêu biết rằng giá gốc của máy tính là 5 triệu đồng.
Câu 37:
Cho hai đại lượng x và y tỉ lệ nghịch với nhau và khi x = 2 thì y = 4.
a) Tìm hệ số tỉ lệ a;
b) Hãy biểu diễn x theo y;
c) Tính giá trị của x khi y = –1 ; y = 2.
Câu 38:
Cho tam giác ABC nội tiếp đường tròn (O); phân giác AD. Vẽ đường tròn (O') đi qua A, D và tiếp xúc với (O). Gọi M, N là giao của AB, AC với (O'). Chứng minh rằng:
a) MN song song với BC.
b) BC là tiếp tuyến của (O').
Câu 39:
Cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D. Gọi K là giao điểm của EB với đường tròn (O) và H là giao điểm của BD và AK.
a) ΔABE là tam giác gì?
b) Chứng minh rằng EH vuông góc với AB.
c) Chứng minh rằng OD vuông góc với AK.
Câu 40:
Cho parabol (P): y = x2 và đường thẳng (d): y = 2mx – 2m + 3
a. Khi m = \(\frac{1}{2}\). Xác định tọa độ giao điểm của (d) và (P)
b. Gọi A(x1,y1) và B(x2,y2) là các giao điểm của (d) và (P). Tìm các giá trị của m để y1 + y2 < 9
Câu 41:
Cho tam giác ABC vuông tại B. Gọi E, F lần lượt là trung điểm của AC,BC. Kẻ Ex song song với BC cắt AB tại M
a) Chứng minh BMEF là hình chữ nhật
b) Gọi K đối xứng với B qua E. Tứ giác BAKC là hình gì? Vì sao?
c) Gọi G đối xứng với E qua F. Tứ giác BGCE là hình gì? Vì sao?
d) Tam giác ABC cần thêm điều kiện gì để tứ giác BGCE là hình vuông?
Câu 42:
Cho tam giác ABC. Các điểm M và N được xác định bởi hệ thức \(\overrightarrow {BM} = \overrightarrow {BC} - 2\overrightarrow {AB} \) và \(\overrightarrow {CN} = x\overrightarrow {AC} - \overrightarrow {BC} \). Xác định giá trị của x để A, M, N thẳng hàng.
Câu 45:
Có bao nhiêu giá trị của x thỏa mãn 60 < x < 95 và x vừa chia hết cho 5, vừa chia hết cho 3.
Câu 48:
Tuổi của Đức 4 năm trước đây bằng một nửa tuổi của Đức 5 năm sau này. Tính tuổi Đức hiện nay?
Câu 49:
Tính \(\lim \frac{{n\sqrt {1 + 3 + 5 + ... + \left( {2n - 1} \right)} }}{{2{n^2} + 1}}\).
Câu 50:
Hai công nhân phải làm một số dụng cụ bằng nhau trong cùng 1 thời gian. Người thứ nhất mỗi giờ làm tăng 2 dụng cụ thì hoàn thành công việc trước thời hạn 2 giờ. Người thứ 2 mỗi giờ làm tăng 4 dụng cụ nên không những hoàn thành công việc trước thời hạn 3 giờ mà còn làm thêm 6 chiếc nữa. Tính số dụng cụ mỗi người được giao.
Câu 51:
Bác Ba cần lát gạch cho một nền nhà hình chữ nhật có chiều dài là 20m và chiều rộng bằng một phần tư chiều dài. Bác Ba muốn lót gạch hình vuông cạnh 4dm lên nền nhà đó nên đã mua gạch bông với giá một viên gạch là 80000 dồng. Hỏi số tiền mà bác Ba phải trả để mua gạch?
Câu 52:
Cho 2 đa thức A(x) = 2x3 – x2 – x + 1 và B(x) = x – 2.
a) Tìm thương và số dư của phép chia đa thức A(x) cho đa thức B(x).
b) Tìm số nguyên x để A(x) chia hết cho B(x).
Câu 53:
Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D.
a) Chứng minh tứ giác AEBM là hình thoi.
b) Gọi I là trung điểm của AM . Chứng minh E, I, C thẳng hàng.
c) Tam giác ABC có thêm điều kiện gì thì AEBM là hình vuông.
Câu 56:
Một con cá có đuôi nặng 250 g, đầu nặng bằng đuôi và nửa thân, thân nặng bằng đầu và đuôi. Hỏi con cá nặng bao nhiêu ki – lô – gam ?
Câu 61:
Xếp ngẫu nhiên 3 quyển sách lý khác nhau, 2 quyển sách toán khác nhau và 4 quyển sách hóa khác nhau thành 1 hàng ngang trên kệ sách. Tính xác suất các sách cùng môn luôn đứng cạnh nhau.
Câu 62:
Cho đường tròn (O) có các dây cung AB, BC, CA. Gọi M là điểm chính giữa của cung nhỏ AB. Vẽ dây MN song song với BC và gọi s là giao điểm của MN và AC. Chứng minh SM = SC và SN = SA.
Câu 63:
Một công ty điện tử sản suất hai loại máy tính trên hai dây chuyền độc lập (loại một và loại hai). Máy tính loại một sản xuất trên dây chuyền một với công suất tối đa 45 máy tính một ngày; máy tính loại hai sản xuất trên dây chuyền hai với công suất tối đa 80 máy tính một ngày. Để sản xuất một chiếc máy tính loại một cần 12 linh kiện và cần 9 linh kiện để sản xuất một máy tính loại hai. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900 linh kiện và tiền lãi bán một chiếc máy loại một là 250.000 đồng; tiền lãi khi bán một chiếc máy loại hai là 180.000 đồng. Hỏi cần sản xuất mỗi loại bao nhiêu máy tính để tiền lãi thu được trong một ngày là nhiều nhất. (Giả thiết rằng tất cả các máy tính sản xuất ra trong ngày đều bán hết).
Câu 64:
Số các số tự nhiên chẵn, có 4 chữ số khác nhau từng đôi một không tận cùng bằng 0 là?
Câu 65:
Có bao nhiêu số tự nhiên gồm 5 chữ số phân biệt sao cho 1, 2, 3 luôn đứng cạnh nhau?
Câu 66:
Cho hình thang cân ABCD có CD = 2AB = 2a,(a > 0), \(\widehat {DAB}\) = 120°, AH vuông góc CD tại H. Tính \(\overrightarrow {AH} \left( {\overrightarrow {CD} - 4\overrightarrow {AD} } \right),\overrightarrow {AC} .\overrightarrow {BH} \).
Câu 67:
Cho đường tròn (O;R) và dây cung MN = \(R\sqrt 3 \). Kẻ OK vuông góc MN tại K.
a) Tính OK theo r.
b) Tính góc \(\widehat {MOK}\) và góc \(\widehat {MON}\).
c) Tính số đo cung nhỏ, cung lớn MN.
Câu 68:
Cho đường tròn (O) đường kính AB. Trên nửa đường tròn đó lấy hai điểm C, D. Kẻ CH vuông góc với AB cắt đường tròn tại điểm thứ hai E. Kẻ AK vuông góc với CD, cắt đường tròn tại điểm thứ hai F. Chứng minh rằng:
a) Hai cung nhỏ CF và DB bằng nhau.
b) DE = BF.
Câu 70:
Một cửa hàng có 28000l xăng. Tuần thứ nhất, cửa hàng bán được 48% số xăng đó. Số xăng trong tuần thứ nhất gấp đôi số xăng bán được tuần thứ hai. Hỏi sau 2 tuần, cửa hàng còn lại bao nhiêu lít xăng?
Câu 72:
Một tổ sản xuất theo kế hoạch phải làm 2400 sản phẩm trong một thời gian quy định, nhưng thực tế nhờ năng xuất lao động tăng nên mỗi ngày tổ đã làm thêm được 6 sản phẩm so với kế hoạch,cho nên chẳng những đã hoàn thành kế hoạch trước 3 ngày mà còn làm thêm được 120 sản phẩm so với kế hoạch. Tìm số sản phẩm mà tổ sản xuất phải làm trong một ngày theo kế hoạch.
Câu 73:
Cho 2 đường thẳng a và b cắt nhau tại điểm O trên đường thẳng a lấy 8 điểm khác nhau không tính điểm O trên đường thẳng b lấy 10 điểm ko tính điểm O. Tính số tam giác có 3 đỉnh là các điểm tính luôn điểm O nằm trên đường thẳng a hay đường thẳng b đã cho.
Câu 74:
Cho đường thẳng d1: y = mx + 2m – 1 ( với m là tham số) và d2: y = x + 1.
a) Với m = 2. Hãy vẽ các đường thẳng d1 và d2 trên cùng 1 mặt phẳng tọa độ . Tìm tọa độ giao điểm của 2 đường thẳng d1 và d2.
b) Tìm giá trị của m để đường thẳng d1 cắt trục hoành tại điểm có hoành độ bằng –3
c) Chứng minh rằng đường thẳng d1 luôn đi qua một điểm cố định với mọi giá trị của m.
Câu 75:
Cho đường tròn (O) và điểm I không nằm trên đường tròn. Qua điểm I kẻ 2 dây cung AB và CD (A nằm giữa I và B, C nằm giữa I và D.
a) So sánh các cặp góc \(\widehat {ACI}\) và \(\widehat {ABD}\), \(\widehat {CAI}\) và \(\widehat {CDB\;}\).
b) Chứng minh các tam giác IAC và IDB đồng dạng.
c) Chứng minh IA.IB = IC. ID.
Câu 76:
Cuối năm 2005, số dân của 1 xã là 7500 người. Nếu tỉ lệ tăng dân số hàng năm là 1,6% thì cuối năm 2006 xã đó có bao nhiêu người?
Câu 77:
Cho tam giác ABC và điểm M thỏa mãn \(3\overrightarrow {MA} - 2\overrightarrow {MB} + \overrightarrow {MC} = \left| {\overrightarrow {MB} - \overrightarrow {MA} } \right|\). Tìm tập hợp M?
Câu 78:
Gọi G là trọng tâm của tam giac ABC. Từ G kẻ các đường thẳng song song với hai cạnh AB và AC, cắt BC lần lượt tại D và E. So sánh ba đoạn thẳng BD, DE, EC.
Câu 81:
Một khu vườn hình chữ nhật có diện tích là 300m2, 2 cạnh tỉ lệ với 4 và 3. Tính chiều dài chiều rộng khu vườn.
Câu 82:
Một trường trung học phổ thông có 4 học sinh giỏi khối 12, có 5 học sinh giỏi khối 11, có 6 học sinh giỏi khối 10. Hỏi có bao nhiêu cách sắp xếp 15 học sinh trên thành một hàng ngang để đón đoàn đại biểu, nếu các học sinh ở cùng một khối thì xếp gần nhau.
Câu 83:
Rút gọn biểu thức P = 1 + \(\frac{{\tan \left( {180^\circ - x} \right)}}{{\sin x.\sin \left( {90^\circ - x} \right)}}\) với x ∈ (0°; 90°).
Câu 86:
Có bao nhiêu cách trao 18 cuốn sách bao gồm 7 cuốn sách toán,6 cuốn sách lý và 5 cuốn sách hóa (các cuốn sách cùng loại thì giống nhau) để làm phần thưởng cho 9 bạn học sinh mỗi bạn nhận được 2 cuốn sách khác thể loại (không tính thứ tự các cuốn sách).
Câu 87:
Diện tích của mạnh đất hình chữ nhật là 2782 m2. Nếu gấp chiều rộng lên hai lần và chiều dài lên ba lần thì diện tích mới là bao nhiêu?
Câu 88:
Biết 48 lít dầu nặng 36 kg. Một can chứa dầu nặng 30 kg. Biết cân nặng của can khi rỗng là 1,5 kg, số lít dầu chứa trong can đó là ?
Câu 89:
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau AB = 6a, AC = 7a, AD = 4a. Gọi M, N, P tương ứng là trung điểm các cạnh BC, CD, DB. Tính thể tích của tứ diện AMNP.
Câu 93:
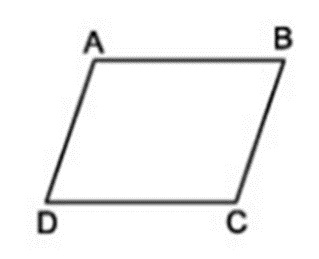
Cho hình thang ABCD có đáy AB, CD. Cho biết AD // BC như hình vẽ. Chứng minh rằng AD = BC, AB = CD.
Câu 94:
Cho tam giác ABC, gọi M và N lần lượt là trung điểm của AB và AC. Trên tia đối của tia NM lấy điểm D sao cho ND = NM.
a) Chứng minh: AD // MC.
b) Chứng minh: BC = 2MN.
Câu 95:
Cho tam giác ABC cân tại A. Gọi M là trung điểm của BC, K là điểm đối xứng với A qua M.
a) Chứng minh tứ giác ABKC là hình thoi.
b) Tam giác ABC cần thêm điều kiện gì thì tứ giác ABKC là hình vuông?
c) Qua A kẻ đường thẳng song song với BC, đường thẳng này cắt đường thẳng CK tại D. Chứng minh AD = BC.
Câu 96:
Cho tam giác ABC vuông tại A (AB < AC) đường cao AH. Từ H vẽ HE và HF lần lượt vuông góc với AB và AC (E thuộc AB, F thuộc AC).
a) Chứng minh: AEHF là hình chữ nhật và AH = EF.
b) Trên tia FC xác định điểm K sao cho FK = AF. Chứng minh tứ giác EHKF là hình bình hành.
c) Biết BC = 5cm, AC = 4 cm. Tính diện tích tam giác ABC
Câu 97:
Từ các chữ số 0, 1, 2, 7, 8, 9 tạo được bao nhiêu số chẵn có 5 chữ số khác nhau?
Câu 98:
Từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một khác nhau sao cho tích ba chữ số đó là một số chẵn?
Câu 100:
Tính \(\lim \left[ {n\left( {\sqrt {{n^2} + 2} - \sqrt {{n^2} - 1} } \right)} \right]\).
Câu 101:
Một phòng họp có 300 ghế ngồi,đc xếp thành một số hàng có số ghế bằng nhau. Buổi họp hôm đó có 378 người đến dự họp nên ban tổ chức đã kê thêm 3 hàng ghế và mỗi xếp thêm 1 ghế, mới đủ chỗ ngồi. Hỏi lúc đầu phòng họp có bao nhiêu hàng ghế và mỗi hàng có bao nhiêu ghế, biết số hàng ghế ban đầu không vượt quá 20
Câu 102:
Trong các hình bình hành có tổng độ dài đáy và chiều cao là 18 cm, hình bình hành nào có diện tích lớn nhất và diện tích đó là bao nhiêu ?
Câu 103:
Trên đường thẳng d lấy ba điểm A,B,C theo thứ tự đó. Trên nửa mặt phẳng bờ d kẻ hai tia Ax, By cùng vuông góc với dt. Trên tia Ax lấy I. Tia vuông góc với CI tại C cắt By tại K. Đường tròn đường kính IC cắt IK tại P.
1) Chứng minh tứ giác CBPK nội tiếp được đường tròn.
2) Chứng mi nh AI.BK = AC.CB.
Câu 105:
Cho tam giác ABC vuông tại A. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, d là tiếp tuyến của đường tròn tại A. Các tiếp tuyến của đường tròn tại B và C theo thứ tự ở D và E.
a) Tính \(\widehat {DOE}\).
b) Chứng minh: DE = BD + CE.
c) Chứng minh: BD.CE = R2.
Câu 106:
A = {1; 2; 3; …; 16}. Bốc ngẫu nhiên 3 phần tử trong A. Tính xác suất để tổng 3 số bốc ra chia hết cho 3.
Câu 107:
Cho đường tròn tâm O bán kính 5cm dây AB = 8 cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh CD = AB.
Câu 108:
Cho dãy số (un) bởi: u1 = 1 và un+1 = 5un + 8 với mọi n ≥ 1.
a) Chứng minh rằng dãy số (vn) với vn = un +2 là một cấp số nhân.
b) Dựa vào kết quả phần a) hãy tìm số hạng tổng quát của dãy số (un).
Câu 109:
Cho khối chóp đều S.ABCD có tất cả các cạnh đều bằng \(a\sqrt 3 \). Tính thể tích V của khối cầu ngoại tiếp hình chóp.
Câu 110:
Cho ΔABCΔABC vuông tại A (AB < AC) và đường cao AH. Từ H kẻ HE ⊥ AB, HF ⊥ AC (E ∈ AB; F ∈ AC).
a) Chứng minh tứ giác AEHF là hình chữ nhật.
b) Gọi D là điểm đối xứng của A qua F. Chứng minh DHEF là hình bình hành.
c) Gọi I là giao điểm của EF và AH; M là trung điểm của BC. Qua A kẻ tia Ax vuông góc với đường thẳng MI cắt tia CB tại K. Chứng minh 4 điểm K, E, I, F thẳng hàng.
Câu 111:
Cho đường tròn (O; R) và dây BC cố định (BC < 2R), BF là đường kính. A là điểm di chuyển trên cung lớn BC (A khác B, C) sao cho tam giác ABC có ba góc nhọn, các đường cao AD và CE của tam giác ABC cắt nhau tại H.
a) Chứng minh AEDC nội tiếp.
b) Chứng minh HF đi qua trung điểm G của đoạn thẳng AC.
Câu 115:
Lãi suất tiết kiệm là 1.2% một tháng. Một người gửi tiết kiệm 8000000 đồng. Hỏi sau hai tháng , cả tiền gửi và tiền lãi là bao nhiêu đồng?
Câu 116:
Một người bỏ ra 4 500 000 đồng tiền vốn mua hoa. Biết rằng người đó lãi 12% tiền vốn. Tính số tiền lãi.
Câu 118:
So sánh A và B biết A = \(\frac{{{{10}^{2020}} + 1}}{{{{10}^{2021}} + 1}}\) và B = \(\frac{{{{10}^{2021}} + 1}}{{{{10}^{2022}} + 1}}\).
Câu 119:
Cho ba đường thẳng y = 2x + 1 (d1); y = x – 1 (d2) và u = (m + 1)x – 2. Tìm điều kiện của tham số m để ba đường thẳng đồng quy.
Câu 120:
Tìm tham số m để ba đường thẳng y = x – 2; y = 2x + m + 1 và y = 3x – 2 đồng quy.
Câu 121:
Cho hình đa diện đều loại {4;3} có cạnh bằng a. Gọi S là tổng diện tích tất cả các mặt của hình đa diện đó. Tính S?
Câu 122:
Tìm giá trị nhỏ nhất của A biết A = \(\frac{{{x^2} - 2x + 2016}}{{{x^2}}},x > 0\).
Câu 126:
Cho hình nón đỉnh S, đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ O đến mặt phẳng (SAB) bằng \(\frac{{a\sqrt 3 }}{3}\), \(\widehat {SAO}\) = 30°, \(\widehat {SAB}\) = 60°. Độ dài đường sinh của hình nón theo a bằng?
Câu 127:
Một chiếc đồng hồ đánh chuông, số tiếng chuông được đánh đúng bằng số mà kim giờ chỉ tại thời điểm đánh chuông. Hỏi một ngày đêm đồng hồ đó đánh bao nhiêu tiếng chuông?
Câu 130:
Cho tam giác ABC có AB = 2, BC = 3, AC = 4. M là trung điểm của BC, đường phân giác trong góc C cắt AM tại I. Gọi K là điểm thuộc đường thẳng AB sao cho KM vuông góc với BI. Tính tỉ lệ \(\frac{{AK}}{{AB}}\).
Câu 131:
Cho biểu thức A = \(\frac{{{a^2} + \sqrt a }}{{a - \sqrt a + 1}} - \frac{{2a + \sqrt a }}{{\sqrt a }} + 1\).
a) Rút gọn A.
b) Tìm a để A = 2.
c) Tìm giá trị nhỏ nhất của A.
Câu 132:
Cho \(\frac{{AB}}{{CD}} = \frac{5}{7}\)và đoạn thẳng AB ngắn hơn CD là 10 cm. Tính độ dài đoạn thẳng AB và CD?
Câu 133:
Trên đường thẳng d , lấy 4 điểm A, B, C, D theo thứ tự đó sao cho cho \(\frac{{AB}}{{BC}} = \frac{3}{5}\), \(\frac{{BC}}{{CD}} = \frac{5}{6}\).
a) Tính tỉ số \(\frac{{AB}}{{CD}}\).
b) Cho biết AD = 28 cm. Tính độ dài các đoạn thẳng AB, BC và CD.
Câu 134:
Cho tam giác ABC. Điểm D trên cạnh AB sao cho 3AD = 2DB. Lấy điểm E trên cạnh AC sao cho DE // BC. Giả sử AC + EC = 16cm. Tính AC, EC và AE.
Câu 135:
Đặt dấu ngoặc một cách thích hợp để tính tổng đại số sau:
a) 942 – 2567 + 2563 – 1942.
b) 13 – 12 + 11 + 10 – 9 + 8 – 7 – 6 + 5 – 4 + 3 + 2 – 1.
Câu 136:
Cha hơn con 32 tuổi. Biết 4 năm nữa tổng số tuổi của 2 cha con là 64 tuổi. Tính tuổi 2 cha con hiện nay ?
Câu 137:
Một công nhân phải làm một số dụng cụ trong một thời gian. Nếu mỗi ngày tăng 3 dụng cụ thì hoàn thành sớm 2 ngày, nếu mỗi ngày làm giảm 3 dụng cụ thì thời gian phải kéo dài 3 ngày. Tính số dụng cụ được giao.
Câu 138:
Một thửa ruộng hình chữ nhật có chu vi là 120m. Tính diện tích thửa ruộng đó nếu biết tăng chiều rộng 5m và giảm chiều dài 5m thì thua ruộng đó thành hình vuông.
Câu 139:
Cho biểu thức A = \(\frac{x}{{2x - 2}} + \frac{{{x^2} + 1}}{{2 - 2{x^2}}}\).
a) Rút gọn biểu thức A.
b) Tìm giá trị của x để A > –1.
Câu 140:
Gọi M là tập hợp các số tự nhiên có ba chữ số lập được từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7. Lấy ngẫu nhiên đồng thời 2 số từ tập M. Xác suất để cả 2 số lấy được đều có chữ số hàng chục nhỏ hơn các chữ số hàng trăm và hàng đơn vị là?
Câu 141:
Một nhà máy dự định sản xuất một số chi tiết máy trong một thời gian đã định, với năng suất 300 chi tiết máy trong một ngày. Nhưng thực tế mỗi ngày đã làm được 400 chi tiết nên đã sản xuất thêm được 600 chi tiết và hoàn thành kế hoạch trước 1 ngày. Tính số chi tiết máy dự định sản xuất.
Câu 142:
Bảng giá cước của hãng taxi được cho như sau: Giá mở cửa 11 000 đồng. Giá tiếp theo từ 0,8km đến 30km là 15 800 đồng/1km. Từ km thứ 31 trở đi giá 12 500 đồng/1km. Quí thời gian chờ từ 5 phút đến 1 giờ là 3000 đồng. Giá trên đã bao gồm thuế VAT.
a) Gọi y (đồng) là số tiền khách phải trả sau khi đi x (km). Lập hàm số của y theo x. (Giả sử không tính thời gian chờ và phí cầu đường, bến bãi).
b) Một hàn khách thuê taxi quãng đường 40km phải trả số tiền là bao nhiêu?
Câu 143:
Cho một số có 4 chữ số khác nhau biết tổng các chữ số là 9. Tính tích của các chữ số đó?
Câu 144:
Cho đoạn thẳng AB và điểm C thuộc đoạn AB sao cho 3AC = 2BC. Biết AB = 10 cm, tính độ dài AC, CB?
Câu 145:
Cho đường tròn (O; 25cm) và hai dây MN // PQ có độ dài theo thứ tự 40 cm và 38 cm. Tính khoảng cách giữa dây MN và PQ?
Câu 149:
Một người đang dự định đi mua xe máy mà muốn chọn 1 trong hai loại xe sau:
Loại 1: Có giá 27 000 000 (đồng) và trung bình số ki–lô–mét đi được mỗi lít xăng là 58 km/lít xăng.
Loại 2: Có giá 30 000 000 (đồng) và trung bình số ki–lô–mét đi được mỗi lít xăng là 62,5 km/lít xăng.
Biết rằng giá trung bình của 1 lít xăng là 18 000 (đồng). Người ta dự tính mua xe máy để sử dụng khoảng 8 năm. Biết rằng mỗi năm người đó đi được khoảng 7 250 km.
Gọi s (đồng) là chi phí từng năm theo thời gian t (năm) của mỗi loại xe (bao gồm tiền mua xe và tiền xăng). Lập hàm số của s theo t.
Câu 150:
Một lớp có 40 học sinh,trong đó nam nhiều hơn nữ.Trong giờ ra chơi,cô giáo đưa cho cả lớp 260000 đồng để mỗi bạn nam mua ly Coca giá 5000 đồng/ly , mỗi mỗi bạn nữ mua một bánh phô mai giá 8000 đồng/cái và được căn tin thối lại 3000 đồng. Hỏi lớp có bao nhiêu học sinh nam và nữ?
Câu 157:
Bà Minh có 3 530 000 đồng với tổng cộng có 74 tờ tiền gồm 3 loại: loại 20 000 đồng loại 50 000 đồng và loại 100 000 đồng . Hỏi mỗi loại có mấy tờ biết rằng số tờ tiền loại 20 000 đồng gấp đôi số tờ tiền loại 100 000 đồng.
Câu 158:
Ba xe ô tô chở 118 tấn hàng tổng cộng hết 50 chuyến. Số chuyến xe thứ nhất chở gấp rưỡi số chuyến thứ 2. Mỗi chuyến xe thứ nhất chở 2 tấn, xe thứ 2 chở 2,5 tấn, xe thứ 3 chở 3 tấn. Hỏi mỗi ô tô chở bao nhiêu chuyến?
Câu 159:
Tìm p biết: \(\frac{{{{\left( {x + y} \right)}^2}}}{{x - y}} = \frac{p}{{{x^2} - {y^2}}}\).
Câu 160:
Cho hình vuông có cạnh bằng 2a. Tính độ dài vectơ \(\left| {\overrightarrow {AC} } \right|\).
Câu 161:
Cho tam giác ABC vuông tại A. Tính góc giữa hai vectơ \(\left( {\overrightarrow {CA} ,\overrightarrow {BC} } \right)\).
Câu 162:
Cho tam giác ABC vuông tại A, AH là đường cao. Kẻ D đối xứng H qua AB, E đối xứng H qua. Gọi I là giao điểm của AB và DH, K là giao điểm của AC và HE.
a) AIHK là hình gì?
b) D, A, E thẳng hàng.
c) BC = BD + CE.
d) SAIHK = a, tính SDHE theo a.
Câu 163:
Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng CD = AB.
Câu 164:
Cách viết nào sau đây là đúng. Tập hợp các ƯC (24;16) là A = {1; 2; 4; 8}.
A. 1 ∉ A.
B. {2; 4} ⸦ A.
C. 8 ⸦ A.
D. 4 ∉ A.
Câu 165:
Hai tổ phải hoàn thành 90 sản phẩm. Do cải tiến kĩ thuật nên tổ 1 vượt 15%, tổ 2 vượt 12% nên cả hai tổ làm được 102 sản phẩm. Hỏi số sản phẩm mỗi tổ được giao?
Câu 166:
Khi nào dùng nhân lượng liên hợp trong giới hạn hữu hạn của hàm số tại một điểm?
Câu 167:
Kết quả đo chiều dài của một cây cầu được ghi là 152m ± 0,2m, điều đó có nghĩa là gì? Tìm sai số tương đối.
Câu 169:
Một phân xưởng có 20 máy đóng gói tự động, trong một ngày đóng gói được 400 sản phẩm. Để đóng gói được 600 sản phẩm một ngày thì phân xưởng đó cần đầu tư thêm bao nhiêu máy? Giả thiết rằng năng suất của các máy là như nhau.
Câu 170:
Một người bắt đầu đi làm được nhận được số tiền lương là 7 000 000 đồng một tháng. Sau 36 tháng người đó được tăng lương 7%. Hằng tháng người đó tiết kiệm 20% lương để gửi vào ngân hàng với lãi suất 0,3%/tháng theo hình thức lãi kép (nghĩa là lãi của tháng này được nhập vào vốn của tháng kế tiếp). Biết rằng người đó nhận lương vào đầu tháng và số tiền tiết kiệm được chuyển ngay vào ngân hàng. Hỏi sau 36 tháng tổng số tiền người đó tiết kiệm được (cả vốn lẫn lãi) là bao nhiêu? (làm tròn đến hàng nghìn).
Câu 171:
Một xưởng sản xuất nước mắm đã sản xuất được 1230 lít nước mắm, người ta muốn đóng vào các can như nhau. Hãy tính và nêu số can nước mắm đóng được trong các trường hợp sau:
|
Số lít mỗi can |
2 lít |
3 lít |
5 lít |
|
Số can |
? |
? |
? |
Câu 174:
Cho A (m; m + 2), B(1;2). Tìm giá trị của m để đoạn thẳng AB có độ dài là 5 đơn vị.