56 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 48)
Haylamdo biên soạn và sưu tầm 56 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
56 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 48)
Câu 1:
Tìm tập xác định D của hàm số y = ln(x – 1).
A. D = (−∞; −1);
B. D = (−1; + ∞);
C. D = (−∞; 1);
D. D = (1; +∞).
Câu 2:
Tìm tập xác định D của hàm số y = ln(x – 3).
A. D = (3; +∞);
B. D = (−∞; + ∞);
C. D = (0; +∞);
D. D = (e; +∞).
Câu 3:
Tìm m để phương trình cos2x + 2(m + 1)sinx − 2m – 1 = 0 có đúng 3 nghiệm x ∈ (0; π).
Câu 4:
Tìm m để phương trình 2sin2x – (2m + 1)sinx + 2m – 1 = 0 có nghiệm thuộc khoảng t ∈ (−1; 0).
Câu 5:
Cho phương trình (m2 + 2)cos2x – 2msin2x + 1 = 0. Để phương trình có nghiệm thì giá trị thích hợp của tham số m là
A. \(\frac{{ - 1}}{2} \le m \le \frac{1}{2}\);
B. −1 ≤ m ≤ 1;
C. \( - \frac{1}{4} \le m \le \frac{1}{4}\);
D. |m| ≥ 1.
Câu 6:
Cho hàm số f(x) = ax4 + bx3 + cx2 (a, b, c ∈ ℝ). Hàm số y = f '(x) có đồ thị như trong hình bên. Số nghiệm thực phân biệt của phương trình 2f(x) + 3 = 0.
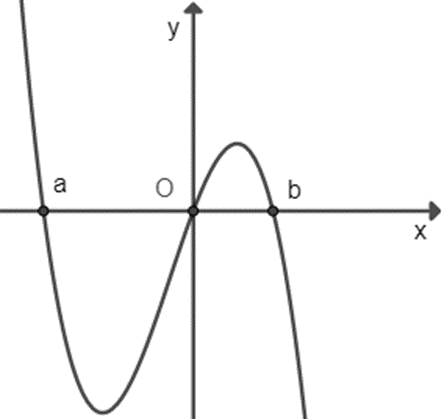
A. 4;
B. 1;
C. 2;
D. 3.
Câu 7:
Cho tứ giác ABCD như hình dưới đây: Điểm E là trung điểm của đoạn thẳng AB. Điểm F là trung điểm của đoạn thẳng BC. Điểm G là trung điểm của đoạn thẳng DC. Điểm H là trung điểm của đoạn thẳng AD. Hỏi tứ giác EFGH là hình gì? Chứng minh điều đó.
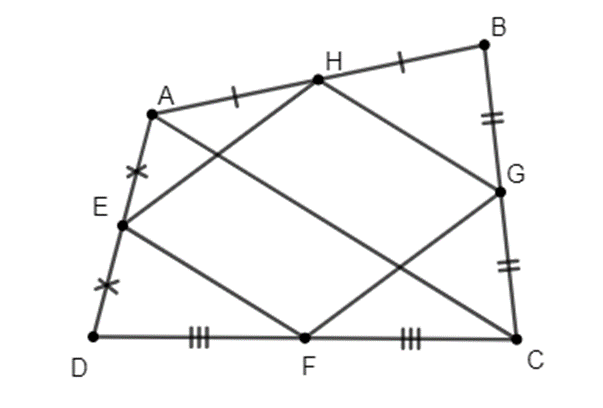
Câu 8:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 – 3(m + 2)x2 + 3(m2 + 4m)x + 1 nghịch biến trên khoảng (0; 1)?
A. 1;
B. 4;
C. 3;
D. 2.
Câu 9:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{1}{4}{x^4} - 14{x^2} + 48x + m - 30} \right|\) trên đoạn [0; 2] không vượt quá 30. Tổng giá trị các phân tử của tập S bằng
A. 108;
B. 136;
C. 120;
D. 210.
Câu 10:
Gọi S là ập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số \(y = \left| {\frac{{{x^2} + mx + m}}{{}}x + 1} \right|\) trên đoạn [1; 2] bằng 2. Số phần tử của tập S là
A. 3;
B. 1;
C. 4;
D. 2.
Câu 11:
Hình bên là đồ thị của ba hàm số y = ax, y = bx, y = cx (0 < a, b, c ≠ 1) được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
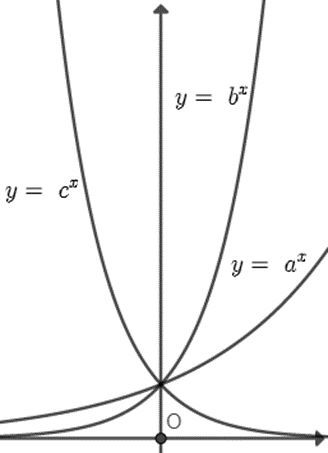
A. a > b > c;
B. c > b > a;
C. a > c > b;
D. b > a > c.
Câu 12:
Hỏi có thể lập được bao nhiêu số tự nhiên có 4 chữ số sao cho trong mỗi số đó, chữ số hàng ngàn lớn hơn hàng trăm, chữ số hàng trăm lớn hơn hàng chục và chữ số hàng chục lớn hơn hàng đơn vị.
A. 221;
B. 209;
C. 210;
D. 215.
Câu 13:
Tìm m để đường thẳng y = mx + 1 cắt đồ thị hàm số \(y = \frac{{x + 1}}{{x - 1}}\) tại hai điểm thuộc nhánh của đồ thị.
A. \(m \in \left( {\frac{{ - 1}}{4}; + \infty } \right)\backslash \left\{ 0 \right\}\);
B. m ∈ (0; +∞);
C. m ∈ (−∞; 0);
D. m = 0.
Câu 14:
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m = 0 có nghiệm \(x \in \left( {\frac{{ - \pi }}{2};0} \right)\).
Câu 15:
Cho phương trình \[4\sin \left( {x + \frac{\pi }{3}} \right).\cos \left( {x - \frac{\pi }{6}} \right) = {a^2} + \sqrt 3 \sin 2x - \cos 2x(1)\]. Gọi n là số giá trị nguyên của tham số a để phương trình (1) có nghiệm. Tính n.
A. n = 5;
B. n = 3;
C. n = 2;
D. n = 1.
Câu 16:
Tập xác đinh của hàm số \(y = {\log _2}\left( {{2^x} - 2} \right) + {\log _{\sqrt 2 }}\frac{1}{{3 - {x^2}}}\) là
A. \(D = \left[ {1;\sqrt 3 } \right]\);
B. \(D = \left( {1;\sqrt 3 } \right)\);
C. \(D = \left( { - \sqrt 3 ;\sqrt 3 } \right)\);
D. \(D = \left( { - \sqrt 3 ;1} \right)\).
Câu 17:
Tập xác định của hàm số y = log2(x2 – 16) + log3(3x – 1 – 9) là
A. D = (−4; 4);
B. \(D = \left( { - \infty ;4} \right) \cup \left( {4;\sqrt 2 } \right)\);
C. D = (3; 4);
D. D = (4; +∞).
Câu 18:
Tìm số các nghiệm nguyên không âm (x; y; z) của phương trình x + y + z = 10.
A. 54;
B. 60;
C. 66;
D. 72.
Câu 19:
Tìm m để đường thẳng y = x + m (d) cắt đồ thị hàm số \(y = \frac{{2x + 1}}{{x - 2}}(C)\) tại hai điểm phân biệt thuôc hai nhánh của đồ thị (C).
A. m ∈ ℝ;
B. \(m \in \mathbb{R}\backslash \left\{ { - \frac{1}{2}} \right\}\);
C. \(m > - \frac{1}{2}\);
D. \(m < - \frac{1}{2}\).
Câu 20:
Cho hàm số y = f( x) có đạo hàm là hàm số y = f’(x) trên R. Biết rằng hàm số y = f ' (x – 2) + 2 có đồ thị như hình vẽ bên dưới. Hàm số y = f( x) nghịch biến trên khoảng nào?
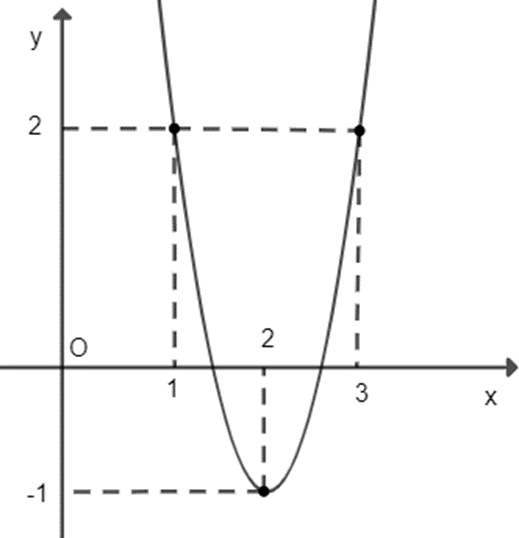
A. (−∞; 2);
B. (−1; 1);
C. \(\left( {\frac{3}{2};\frac{5}{2}} \right)\);
D. (2; +∞).
Câu 21:
Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của x?
A. \[y = \sqrt {2x - 1} \];
B. y = \({\left( {2{x^2} + 1} \right)^{ - \frac{1}{3}}}\);
C. y = (1 – 2x)-3;
D. y = \({\left( {1 + 2\sqrt x } \right)^3}\).
Câu 22:
Cho hình chop S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy; góc giữa SC và mặt phẳng đáy bằng 45°. Thể tích khối chóp S.ABCD bằng
A. \(\frac{{{a^3}\sqrt 3 }}{{12}}\);
B. \(\frac{{{a^3}\sqrt 3 }}{9}\);
C. \(\frac{{{a^3}\sqrt 5 }}{{24}}\);
D. \(\frac{{{a^3}\sqrt 5 }}{6}\).
Câu 23:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết \(\frac{{{V_{S.AHB}}}}{{{V_{S.ACB}}}} = \frac{{16}}{{19}}\). Tính Thể tích của khối chóp S.ABC.
Câu 24:
Cho hình vuông ABCD có cạnh bằng a và có diện tích S1. Nối 4 điểm A1; B1; C1; D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích, … , S100 (tham khảo hình bên). Tính tổng S = S1 + S2 + S3 + … + S100.
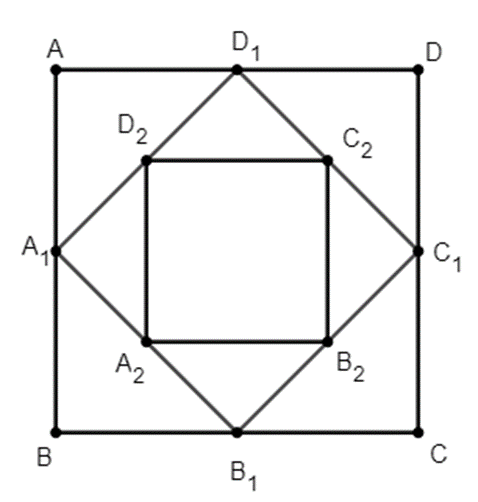
Câu 25:
Cho tam giác đều ABC cạnh a, điểm M là trung điểm BC. Dựng các vectơ sau và tính độ dài của chúng.
a) \(\frac{1}{2}\overrightarrow {CB} + \overrightarrow {MA} \);
b) \(\overrightarrow {BA} - \frac{1}{2}\overrightarrow {BC} \);
Câu 26:
Gọi S là tập hợp các số tự nhiên có ba chữ số (không nhất thiết khác nhau) được lập từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9. Chọn ngẫu nhiên một số \[\overline {abc} \] từ S. Tính xác suất để số được chọn thỏa mãn a ≤ bc.
A. \(\frac{1}{6}\);
B. \(\frac{{11}}{{60}}\);
C. \(\frac{{13}}{6}\);
D. \(\frac{9}{{11}}\).
Câu 27:
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số được lập từ tập hợp X = {0; 1; 2; 3; 4; 5; 6; 7}. Rút ngẫu nhiên một số thuộc tập S. Tính xác suất để rút được số mà trong số đó, chữ số đứng sau luôn lớn hơn hoặc bằng chữ số đứng trước.
A. \(\frac{2}{7}\);
B. \(\frac{{11}}{{64}}\);
C. \(\frac{3}{{16}}\);
D. \(\frac{3}{{32}}\).
Câu 28:
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(1; 2; 3). Phương trình của mặt phẳng (P) là:
A. x + 2y + 3z – 14 = 0;
B. x + 2y + 3z + 14 = 0;
C. \(\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1\);
D. \(\frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 0\).
Câu 29:
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C; trực tâm tam giác ABC là H(4; 5; 6). Phương trình của mặt phẳng (P) là:
A. 4x + 5y + 6z – 77 = 0;
B. 4x + 5y + 6z + 14 = 0;
C. \(\frac{x}{4} + \frac{y}{5} + \frac{z}{6} = 1\);
D. \(\frac{x}{4} + \frac{y}{5} + \frac{z}{6} = 0\).
Câu 30:
Ba số hạng đầu tiên theo lũy thừa tăng dần của x trong khai triển của
(1 + 2x)10 là
A. 1; 45x; 120x2;
B. 1; 4x; 4x2;
C. 1; 20x; 180x2;
D. 10; 45x; 120x2.
Câu 31:
Cho hàm số y = (x – m)3 – 3x + m2 có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a; b) là điểm cực đại của (Cm) ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của (Cm) ứng với một giá trị khác của m. Tổng S = 2018a + 2020b bằng
A. 504;
B. −504;
C. 12 504;
D. 5 004.
Câu 32:
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A. \(\frac{2}{5}\);
B. \(\frac{1}{{20}}\);
C. \(\frac{3}{5}\);
D. \(\frac{1}{{10}}\).
Câu 33:
Cho hai dãy ghế đối diện nhau mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh, gồm 5 nam, 5 nữ ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
A. \(\frac{1}{{252}}\);
B. \(\frac{1}{{945}}\);
C. \(\frac{8}{{63}}\);
D. \(\frac{4}{{63}}\).
Câu 34:
Cho ba điểm A, B, C cùng thuộc một mặt cầu và biết rằng \(\widehat {ACB} = 90^\circ \). Khẳng định nào sau đây là đúng?
A. AB luôn là đường kính của mặt cầu đã cho;
B. Luôn luôn có một đường tròn thuộc mặt cầu ngoại tiếp tam giác ABC;
C. Tam giác ABC vuông cân tại C;
D. AB là đường kính của một đường tròn lớn trên mặt cầu đã cho.
Câu 35:
Cho tam thức f(x) = ax2 + bx + c, (a ≠ 0), ∆ = b2 – 4ac. Ta có f(x) ≤ 0, ∀x ∈ ℝ khi và chỉ khi:
A. \(\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\);
B. \(\left\{ \begin{array}{l}a \le 0\\\Delta < 0\end{array} \right.\);
C. \(\left\{ \begin{array}{l}a < 0\\\Delta \ge 0\end{array} \right.\);
D. \(\left\{ \begin{array}{l}a > 0\\\Delta \le 0\end{array} \right.\).
Câu 36:
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng 3 cm. Gọi M là trung điểm của AB. DM cắt AC tại N. Tính diện tích tam giác AMN.
A. 4 cm2;
B. 10 cm2;
C. 2 cm2;
D. 1 cm2.
Câu 37:
Cho hình bình hành ABCD, O là giao điểm của hai đường thẳng AC và BD. Vectơ chỉ có một vecto đối mà điểm đầu và điểm cuối là hai trong năm điểm A; B; C; D; O là
A. \(\overrightarrow {AB} \);
B. \(\overrightarrow {AC} \);
C. \(\overrightarrow {AD} \);
D. \(\overrightarrow {AO} \).
Câu 38:
Cho hình bình hành ABCD, giao điểm của hai đường chéo là O. Tìm mệnh đề sai trong các mệnh đề sau:
A. \(\overrightarrow {CO} - \overrightarrow {OB} = \overrightarrow {BA} \);
B. \(\overrightarrow {AB} - \overrightarrow {BC} = \overrightarrow {DB} \);
C. \(\overrightarrow {DA} - \overrightarrow {DB} = \overrightarrow {OD} - \overrightarrow {OC} \);
D. \(\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \).
Câu 39:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Cạnh bên \(SA = a\sqrt 6 \) vuông góc với đáy (ABCD). Tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.
A. 8πa2;
B. 2 πa2;
C. 2a2;
D. \({a^2}\sqrt 2 \).
Câu 40:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), tam giác ABC vuông tại B. Biết SA = 2a, AB = a, \(BC = a\sqrt 3 \). Tính bán kính R của mặt cầu ngoại tiếp hình chóp đã cho.
Câu 41:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông cân tại B, biết SA = AC = 2a. Thể tích khối chóp S.ABC là
A. \({V_{S.ABC}} = \frac{2}{3}{a^3}\);
B. \({V_{S.ABC}} = \frac{{{a^3}}}{3}\);
C. VS.ABC = 2a3;
D. \({V_{S.ABC}} = \frac{{4{a^3}}}{3}\).
Câu 42:
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, cạnh AB = 3. Cạnh bên SA = 4 và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
A. \(\sqrt {34} \);
B. 6;
C. \(\frac{{\sqrt {34} }}{2}\);
D. \(2\sqrt 3 \).
Câu 43:
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết AB = BC = a, AD = 2a và SA vuông góc với mặt phẳng (ABCD) và \(SA = a\sqrt 2 \). Gọi M là trung điểm AD. Khoảng cách giữa hai đường thẳng BM và SC bằng
A. \(\frac{a}{2}\);
B. a;
C. \(\frac{{a\sqrt 2 }}{2}\);
D. \(a\sqrt 2 \).
Câu 44:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B với AC = a, biết SA ⊥ (ABC) và SB với đáy một góc 60. Thể tích khối chóp S.ABC là
A. \(V = \frac{{{a^3}\sqrt 6 }}{{24}}\);
B. \(V = \frac{{{a^3}\sqrt 3 }}{{24}}\);
C. \(V = \frac{{{a^3}\sqrt 6 }}{8}\);
D. \(V = \frac{{{a^3}\sqrt 6 }}{{48}}\).
Câu 45:
Cho hình chóp S.ABC có đáy là tam giác đều cạnh 1, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích của khối cầu ngoại tiếp hình chóp đã cho.
Câu 46:
Cho hình lăng trụ đều ABC.A'B'C' , biết góc giữa hai mặt phẳng (A'BC) và (A'B'C') bằng 45°, diện tích tam giác A'BC bằng \({a^2}\sqrt 6 \). Tính diện tích xung quanh của hình trụ ngoại tiếp hình lăng trụ.
Câu 47:
Cho nửa đường tròn tâm O đường kính AB. Ax là tia tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB), từ điểm C trên nửa đường tròn (C khác A, B) vẽ tiếp tuyến CM cắt Ax tại M. Chứng minh MA2 = MQ.MB.
Câu 48:
Hỏi có bao nhiêu giá trị m nguyên trong đoạn [−2017; 2017] để phương trình logmx = 2log(x + 1) có nghiệm duy nhất?
A. 2017;
B. 4014;
C. 2018;
D. 4015.
Câu 50:
Tứ diện ABCD. Gọi M là trung điểm của BC. N là điểm nằm trên đoạn thẳng AB sao cho NB = 2NA, P là điểm nằm trên đoạn thẳng CD sao cho PC = 3PD, S là giao điểm của BD và MP, Q là giao điểm của SN và AD. Tính tỉ số \(\frac{{QD}}{{QA}}\).
Câu 51:
Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau mà các chữ số đều là số chẵn?
A. 48;
B. 60;
C. 360;
D. 80.
Câu 53:
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số được lập từ tập X = {0; 1; 2; 3; 4; 5; 6; 7}. Rút ngẫu nhiên một số thuộc tập S. Tính xác suất để rút được số mà trong số đó, chữ số đứng sau luôn lớn hơn hoặc bằng chữ số đứng trước
Câu 54:
Trong không gian với hệ tọa độ Oxyz , đường thẳng d đi qua điểm A(1; 2; 3) và vuông góc với mặt phẳng (P): 2x + 2y + z + 2017 = 0 có phương trình là
A. \(\frac{{x + 2}}{1} = \frac{{y + 2}}{2} = \frac{{z + 1}}{3}\);
B. \(\frac{{x - 2}}{1} = \frac{{y - 2}}{2} = \frac{{z - 1}}{3}\);
C. \(\frac{{x + 1}}{2} = \frac{{y + 2}}{2} = \frac{{z + 3}}{1}\);
D. \(\frac{{x - 1}}{2} = \frac{{y - 2}}{2} = \frac{{z - 3}}{1}\).
Câu 55:
Tìm tất cả các giá trị của m để phương trình: x4 – 2(m – 1)x2 + 4m – 8 = 0 có 4 nghiệm phân biệt.
A. m > 2 và m ≠ 3;
B. m > 2;
C. m > 1 và m ≠ 3.
D. m > 3.
Câu 56:
Tìm giá trị thực của tham số m để đường thẳng d: y = (2m – 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 – 3x2 + 1.

