65 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 67)

Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu thứ nhất chạy với tốc độ 30 km/h, tàu thứ hai chạy với tốc độ 40 km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

Hai chiếc tàu thủy cùng xuất phát từ một vị trí A, đi thẳng theo hai hướng tạo với nhau góc 60°. Tàu B chạy với tốc độ 20 hải lí một giờ. Tàu C chạy với tốc độ 15 hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí? Kết quả gần nhất với số nào sau đây?

Tính đạo hàm của hàm số  $y=\frac{x+1}{4^x}$.

. Tính đạo hàm của hàm số  $y=\frac{x-1}{4^x}$.

Một cột đèn có bóng trên mặt đất dài 7,5 m. Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 42°. Tính chiều cao của cột đèn (làm tròn đến chữ số thập phân thứ ba).

Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào sau đây sai?

Cho lục giác đều ABCDEF và O là tâm của nó. Đẳng thức nào dưới đây là đẳng thức sai?

Cho các tập hợp khác rỗng $A=\left[m-1;\frac{m+3}{2}\right]$  và B = (−∞; −3) È [3; +∞). Tìm tập hợp các giá trị thực của m để A Ç B ¹ 0.

Tìm tất cả các giá trị thực của tham số m sao cho hàm số  $y=f\left(x\right)=\frac{m{x}^3}{3}+7m{x}^2+14x-m$ giảm trên nửa khoảng [1; +∞)?

Xác định các giá trị của tham số m để hàm số y = x³ − 3mx² − m nghịch biến trên khoảng (0; 1)?

Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị nhỏ nhất của hàm số y = |x² − 2x + m| trên đoạn [0; 3] bằng 5. Tính tổng tất cả các phần tử của S.

Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị nhỏ nhất của hàm số y = f (x) = 4x² − 4mx + m² − 2m trên đoạn [−2; 0] bằng 3. Tính tổng T các phần tử của S.

Phép vị tự tỉ số k = 2 biến tam giác ABC có số đo các cạnh 3, 4, 5 thành tam giác A'B'C' có diện tích là giá trị nào sau đây?

Cho tam giác ABC có diện tích S. Phép vị tự tỉ số k = −2 biến tam giác ABC thành tam giác A'B'C' có diện tích S'. khi đó tỉ số  $\frac{S\text{'}}{S}$ bằng bao nhiêu?

Giá trị lớn nhất của biết thức F (x; y) = x + 2y với điều kiện $\left\{\begin{array}{l}0\le y\le 4\\ x\ge 0\\ x-y-1\le 0\\ x+2y-10\le 0\end{array}\right.$  là

Tam giác ABC có AB = AC = a và  $\widehat{BAC}=120°$. Tính  $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|$.

Cho hình chữ nhật ABCD và I là giao điểm của hai đường chéo. Tìm tập hợp các điểm M thỏa mãn  $\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MC}+\overrightarrow{MD}\right|$.

Cho hai đường thẳng d và d' song song với nhau. Có bao nhiêu phép tịnh tiến biến d thành d'?

Cho các điểm phân biệt A, B, C. Đẳng thức nào sau đây đúng?

Cho 2 tập hợp A = (−2; 5] và B = [2m − 3; 2m + 3]. Tìm m để A giao B là một tập có độ dài bằng 5.

Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm của AB, N là điểm đối xứng với C qua D. Tính độ dài véc tơ  $\overrightarrow{MN}$.

Cho parabol có phương trình y = x² − 3x + 2. Xác định tọa độ đỉnh của Parabol.

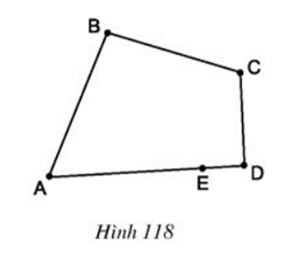
Tại sao hình gồm năm đoạn thẳng AB, BC, CD, DE, EA ở hình 118 không phải là đa giác?

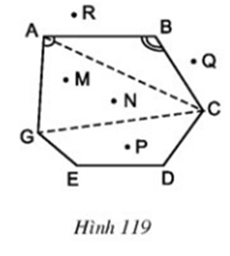
Quan sát đa giác ABCDEG ở hình 119 rồi điền vào chỗ trống trong các câu sau:

Các đỉnh là các điểm: A, B., …

Các đỉnh kề nhau là: A và B, hoặc B và C, hoặc …

Các cạnh là các đoạn thẳng: AB, BC, …

Các đường chéo là các đoạn thẳng nối hai đỉnh không kề nhau: AC, CG, …

Các góc là:  $\widehat{A},\widehat{B},\mathrm{...}$

Các điểm nằm trong đa giác (các điểm trong của đa giác) là: M, N, …

Các diểm nằm ngoài đa giác (các điểm ngoài của đa giác) là: Q, …

Cho hai tập khác rỗng A = (m − 1; 4]; B = (−2; 2m + 2), m Î ℝ. Tìm m để A Ç B ¹ Æ.

Cho hai tập khác rỗng A = (m − 1; 4]; B = (−2; 2m + 2), m Î ℝ. Tìm m để:

a) A Ì  B

b) B Ì A

Cho hình lập phương ABCD.A'B'C'D' có  $A\text{'}C=a\sqrt{3}$. Tính thể tích của hình lập phương.

Cho hình lập phương ABCD.A'B'C'D' có đường chéo bằng  $a\sqrt{3}.$ Tính thể tích khối chóp A'.ABCD.

Cho A là tập hợp tất cả các nghiệm của phương trình x² − 4x + 3 = 0; B là tập hợp các số có giá trị tuyệt đối nhỏ hơn 4. Khẳng định nào sau đây đúng?

Cặp số nào sau đây là nghiệm của hệ bất phương trình  $\left\{\begin{array}{l}x-2y<0\\ x+3y>-2\\ -x+y<3\end{array}\right.$

Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc a với 0 ≤ a < 2p, biến tam giác trên thành chính nó?

Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc a, 0 ≤ a ≤ 2p biến tam giác trên thành chính nó?

Trên mặt phẳng tọa độ Oxy, cho điểm A(4; 5). Hãy xác định vị trí tương đối của đường tròn (A; 5) và các trục tọa độ.

Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.

Có ba chiếc hộp A, B, C mỗi chiếc hộp chứa ba chiếc thẻ được đánh số 1, 2, 3. Từ mỗi hộp rút ngẫu nhiên một chiếc thẻ. Gọi P là xác suất để tổng số ghi trên ba tấm thẻ là 6. Tìm giá trị của P.

Có 3 chiếc hộp A, B, C. Hộp A chứa 4 bi đỏ, 3 bi trắng. Hộp B chứa 3 bi đỏ, 2 bi vàng. Hộp C chứa 2 bi đỏ, 2 bi vàng. Lấy ngẫu nhiên một hộp từ 3 hộp này, rồi lấy ngẫu nhiên một bi từ hộp đó. Tính xác suất để lấy được một bi đỏ.

Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tính tỉ số  $\frac{R}{r}$.

Cho hai đường thẳng d và d' song song có bao nhiêu phép tịnh tiến biến đường thẳng d thành đường thẳng d'?

Một hộp đựng 20 viên bi khác nhau được đánh số từ 1 đến 20. Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại. Hỏi có bao nhiêu cách lấy để kết quả thu được là một số chia hết cho 3?

Một hộp có 20 viên bi được đánh số từ 1 đến 20. Có bao nhiêu cách lấy ra 5 viên sao cho có đúng 3 viên bi lẻ, 2 chẵn trong đó có 1 viên bi chia hết cho 4.

Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?

Nếu tam giác ABC có a² < b² + c² thì

Cho tam giác ABC có a² + b² − c² > 0. Khi đó:

Có hai học sinh lớp A, ba học sinh lớp B và bốn học sinh lớp C xếp thành một hàng ngang sao cho giữa hai học sinh lớp A không có học sinh nào lớp B. Hỏi có bao nhiêu cách xếp hàng như vậy?

Cho DABC và DA'B'C' đồng dạng với nhau theo tỉ số k. Chọn câu sai.

Cho hai tam giác A'B'C' và ABC đồng dạng với nhau theo tỉ số k. Chứng minh rằng tỉ số chu vi của hai tam giác cũng bằng k.

Có 12 người xếp thành một hàng dọc (vị trí của mỗi người trong hàng là cố định), Chọn ngẫu nhiên 3 người trong hàng. Tính xác suất để 3 người được chọn không có 2 người đứng nào cạnh nhau.

Kết quả (b; c) của việc gieo con xúc sắc cân đối và đồng chất hai lần trong đó b là số chấm xuất hiện trong lần gieo đầu, c là số chấm xuất hiện trong lần gieo thứ hai, được thay vào phương trình bậc hai: x² + bx + c = 0. Tính xác suất để: phương trình có nghiệm.

Kết quả (b; c) của việc gieo con xúc sắc cân đối và đồng chất hai lần trong đó b là số chấm xuất hiện trong lần gieo đầu, c là số chấm xuất hiện trong lần gieo thứ hai, được thay vào phương trình bậc hai: x² + bx + c = 0. Tính xác suất để phương trình bậc hai đó vô nghiệm.

Hình nào sau đây không có tâm đối xứng?

Hình nào dưới đây không có tâm đối xứng?

Biểu thức F (x; y) = y − x đạt giá trị nhỏ nhất với điều kiện  $\left\{\begin{array}{l}2x-y\ge 2\\ x-2y\le 2\\ x+y\le 5\\ x\ge 0\end{array}\right.$ tại điểm M. Tìm tọa độ của điểm M.

Cho tam giác ABC, trọng tâm là G. Phát biểu nào là đúng?

Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = xe^x, y = 0, x = 0, x = 1 xung quanh trục Ox là: 

Biết rằng phương trình 2log (x + 2) + log 4 = log x + 4log 3 có hai nghiệm phân biệt x₁, x₂, (x₁ < x₂). Tính  $P=\frac{x_1}{x_2}$.

Tìm tất cả các giá trị của tham số m để phương trình (m − 2)x² + 2(2m − 3) x + 5m − 6 = 0 vô nghiệm?

Tìm tất cả các giá trị của tham số m để bất phương trình (m² + m − 6)x ≥ m + 1 có nghiệm.

Một thầy giáo có 10 cuốn sách khác nhau trong đó có 4 cuốn sách Toán, 3 cuốn sách Lí, 3 cuốn sách Hóa. Thầy muốn lấy ra 5 cuốn và tặng cho 5 em học sinh A, B, C, D, E mỗi em một cuốn. Hỏi thầy giáo có bao nhiêu cách tặng cho các em học sinh sao cho sau khi tặng xong, mỗi một trong ba loại sách trên đều còn ít nhất một cuốn.