94 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án (Phần 85)
Haylamdo biên soạn và sưu tầm 94 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
94 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án (Phần 85)
Câu 1:
Cho đường tròn (O) đường kính AB. Qua trung điểm E của OB kẻ một đường thẳng vuông góc với OB, cắt đường tròn (O) ở M và N. Kẻ dây MP song song với AB. Gọi I là điểm chính giữa của cung nhỏ PM. Gọi K là giao điểm của OI và PM. Chứng minh rằng:
a)
b) Tứ giác OKME là hình chữ nhật.
c) P, O, N thẳng hàng và KE // PN.
Câu 4:
Cho tam giác ABC. Hai điểm M và N di chuyển sao cho . Chứng minh MN luôn đi qua một điểm cố định.
Câu 6:
Cho hình bình hành ABCD. Ở phía ngoài hình bình hành, vẽ các hình vuông ABEF và ADGH. Chứng minh:
a) ΔAHF = ΔADC.
b) AC ⊥ HF.
Câu 7:
Cho tứ giác ABCD. M, N là trung điểm của AC và BD.
Chứng minh: AB2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4MN2.
Câu 8:
Cho tam giác nhọn ABC. Vẽ ra phía ngoài của tam giác này các tam giác ABD và tam giác ACE vuông cân tại A. Gọi M là trung điểm của DE. Chứng minh rằng hai đường thẳng MA và BC vuông góc với nhau.
Câu 9:
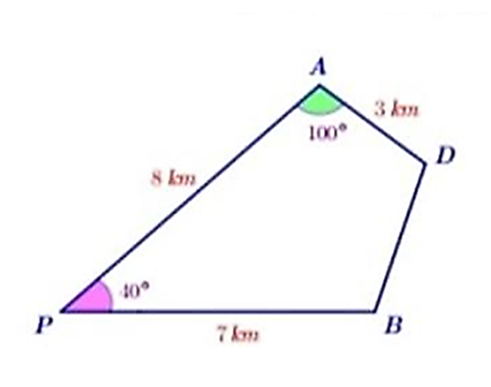
Hai bạn An và Hưng cùng xuất phát từ điểm P, đi theo hai hướng khác nhau và tạo với nhau một góc 40° để đến đích là điểm D. Biết rằng họ dừng lại để ăn trưa lần lượt tại A và B (như hình vẽ minh hoạ). Hỏi Hưng phải đi bao xa nữa để đến được đích?
Câu 11:
Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 1,8cm, HC = 3,2cm
a) Tính AH, AB, AC.
b) Tính góc B, C (làm tròn đến độ).
c) Tia phân giác góc B cắt AC tại D. Tính BD.
d) Chứng minh rằng:Câu 13:
Cho tam giác ABC, dựng ra phía ngoài các hình vuông ABGD và ACEF, vẽ đường cao AH, kéo dài HA gặp DF tại I. Chứng minh: DI = IF.
Câu 16:
Cho tam giác cân ABC (AB = AC), phân giác BD và CE. Gọi I là trung điểm của BC, J là trung điểm của ED, O là giao điểm của BD và CE.
Chứng minh:
a) Tứ giác BEDC là hình thang cân.
b) BE = ED = DC.
c) Bốn điểm A, I, O, J thẳng hàng.
Câu 17:
Cho đường tròn tâm O bán kính R và một điểm A nằm ngoài đường tròn. Qua A kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Vẽ tia Ax nằm giữa tia AB và tia AO cắt đường tròn (O) tại hai điểm C và D (C nằm giữa A và D). Gọi M là trung điểm của dây CD, kẻ BH vuông góc với AO tại H.
a, Tính tích OH.OA theo R.
b, Chứng minh 4 điểm A, B, M, O cùng thuộc một đường tròn.
c, Gọi E là giao điểm của OM với HB. Chứng minh ED là tiếp tuyến của đường tròn (O;R).
Câu 20:
Số học sinh khối 6 của một trường trong khoảng từ 400 đến 500 em. Nếu xếp hàng 7 em thì thừa ra 3 em, còn nếu xếp hàng 6 em, 8 em hoặc 10 em thì vừa đủ. Hỏi số học sinh khối 6 của trường là bao nhiêu em?
Câu 22:
Cho A = 2 + 22 +....... + 260.
a) Thu gọn tổng A.
b) Chứng tỏ rằng: A chia hết cho 3, 5, 7.
Câu 23:
Chứng minh rằng nếu chia hết cho 11 thì cũng chia hết cho 11 (biết rằng là số tự nhiên có hai chữ số; là số tự nhiên có 4 chữ số).
Câu 26:
Đội văn nghệ có 36 bạn, được xếp thành các hàng có số người bằng nhau. Hỏi có thể có những cách xếp hàng nào, biết mỗi hàng có từ 4 đến 12 bạn.
Câu 32:
A. Hai đường thẳng cùng song song với một đường thẳng thứ ba thì song song với nhau.
B. Hai đường thẳng song song nhau nếu chúng không có điểm chung.
C. Hai đường thẳng cùng song song với một mặt phẳng thì song song với nhau.
D. Không có mặt phẳng nào chứa cả hai đường thẳng a và b thì ta nói a và b chéo nhau.
Câu 34:
Cho hình chóp S.ABCD, đáy là hình bình hành ABCD. Gọi M, N lần lượt là trung điểm SA, CD. Chứng minh MN // (SBC).
Câu 35:
Hiện nay mẹ hơn con 24 tuổi. Tuổi mẹ và tuổi con cộng lại là 56. Hỏi hiện nay mẹ bao nhiêu tuổi? Con bao nhiêu tuổi?
Câu 36:
Ông A vay ngắn hạn ngân hàng 100 triệu đồng với lãi suất 12%/năm. Ông muốn hoàn nợ cho ngân hàng theo cách: Sau đúng 1 tháng kể từ ngày vay, ông bắt đầu hoàn nợ; hai lần hoàn nợ liên tiếp cách nhau đúng một tháng, số tiền hoàn nợ ở mỗi lần là như nhau và trả hết tiền nợ sau đúng ba tháng kể từ ngày vay. Hỏi, theo cách đó số tiền m mà ông A sẽ phải trả cho ngân hàng trong mỗi lần hoàn nợ là bao nhiêu? Biết rằng lãi xuất ngân hàng không thay đổi trong thời gian ông A hoàn nợ.
Câu 39:
Từ 1 điểm A ở bên ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Chứng minh OA là trung trực của đoạn BC.
Câu 44:
Một ô tô chạy 100km hết 12 lít xăng. Hỏi cần bao nhiêu lít xăng khi ô tô chạy quãng đường thứ nhất 138km và quãng đường thứ hai 162km?
Câu 45:
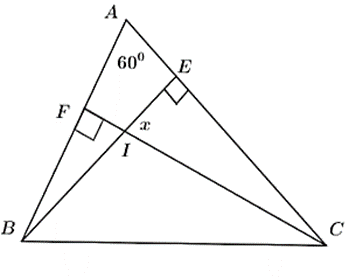
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N. Tính số đo góc
Câu 49:
Cho ∆ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Hỏi bằng vecto nào?
Câu 50:
Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm của AB, AC, BC. Xác định hiệu
Câu 56:
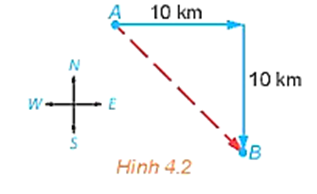
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp 10 km về hướng nam thì tới đảo B (H.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải dài bao nhiêu kilômét?
Câu 57:
Tìm số tự nhiên n có 3 chữ số khác nhau biết rằng nếu xóa bất kì chữ số nào của nó ta cũng được một số là ước của n.
Câu 58:
Tập giá trị của hàm số y = 2sin2x – sinx – 1 là đoạn [m; M]. Khi đó 8m – 3M bằng?
Câu 59:
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3 + 2x2 + (m − 3)x + m
có hai điểm cực trị và điểm M(9; −5) nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị.
Câu 60:
Trên mặt phẳng tọa độ Oxy cho đường thẳng d: y = (2m + 10)x - 4m - 1 và điểm A(-2;3). Tìm m để khoảng cách từ A đến đường thẳng lớn nhất.
Câu 63:
Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC. Chứng minh BC.BE.CF = AH3.
Câu 64:
Cho góc . Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC.
b) DEAB = DECD.
c) OE là tia phân giác của góc xOy.
Câu 65:
cho hình bình hành ABCD, đường chéo AC lớn hơn đường chéo BD, kẻ CH vuông góc với AD, CK vuông góc với AB.
a, Chứng minh tam giác BCK đồng dạng tam giác DCH.
b, Chứng minh tam giác CKH đồng dạng tam giác BCA.
c, Chứng minh HK = AC.sin
d, Tính diện tích của tứ giác AKCH nếu , AB = 4cm, AC = 5cm.
Câu 66:
Cho hình bình hành ABCD. Đặt . Gọi G là trọng tâm của tam giác ABC. Biểu thị các vectơ theo hai vectơ
Câu 67:
Cho tam giác ABC có M là trung điểm của cạnh BC. Vẽ các điểm F, E, G sao cho B, M, C theo thứ tự là trung điểm của AF, AE và AG. Chứng minh ba điểm F, E, G thẳng hàng.
Câu 68:
Cho tam giác ABC nhọn đường cao AH. E, F là hình chiếu của H lên AB, AC. Khi SAHE = 4cm2, SBHE = 1cm2. Tính AB biết EH = 2 cm.
Câu 69:
Cho ∆ ABC nhọn, đường cao AH. Kẻ HE ⊥ AB (E ∈ AB), HF ⊥ AC (F ∈ AC).
a) Chứng minh: ∆AEH ∽ ∆AHB. Từ đó suy ra AH2 = AE.AB.
b) Chứng minh AE. AB = AF.AC.
c) Cho chu vi các ∆AEF và ∆ACB lần lượt là 20 cm và 30 cm. Tính diện tích ∆AEF và ∆ACB biết diện tích ∆ACB lớn hơn diện tích ∆AEF là 25 cm2.
Câu 70:
Cho tam giác ABC vuông tại A, đường cao AH kẻ HE, HF lần lượt vuông góc với AB, AC
a) Chứng minh
b) Chứng minh
Câu 71:
Một cung lượng giác trên đường tròn định hướng có độ dài bằng một nửa bán kính. Số đo theo rađian của cung đó là?
Câu 72:
Một sân trường hình chữ nhật có nửa chu vi là 120 m. Chiều rộng bằng chiều dài. Hỏi diện tích của sân trường đó bằng bao nhiêu mét vuông, bao nhiêu ha?
Câu 78:
Cho hình bình hành ABCD. Vẽ AE ⊥ BC tại E, DF ⊥ AB tại F. Biết AE = DF. Chứng minh rằng tứ giác ABCD là hình thoi.
Câu 80:
Tìm GTLN của a2 + b2 + c2 biết a, b, c thỏa mãn 1 ≤ a, b, c ≤ 2 và a + b + c = 6.
Câu 82:
Câu 83:
Trong mặt phẳng tọa độ Oxy cho tam giác ABC với A(1;3); B(-2;2); C(-1;-3). Tính chu vi và diện tích tam giác ABC.
Câu 84:
Cho a, b, c là 3 số nguyên dương thỏa mãn tổng của 160 và bình phương của a bằng tổng của 5 và bình phương của b. Tổng của 320 và bình phương của a bằng tổng của 5 và bình phương của c. Tìm a
Câu 85:
Cho 2 số thực dương a, b thỏa mãn a2 + 2ab + 2b2 – 2b = 8.
Chứng minh rằng 0 < a + b ≤ 3.
Câu 86:
Câu 87:
Cho các số thực a, b, c sao cho a + b + c = 3; a2 + b2 + c2 = 29 và abc = 11. Tính a5 + b5 + c5.
Câu 90:
Giả sử a, b là 2 số thực phân biệt thỏa mãn: a2 + 3a = b2 + 3b = 2. Chứng minh rằng a3 + b3 = -45.
Câu 91:
Cho hai tập hợp A = (-1;2] và B = {x ∈ R| mx ≥ 1} (với m là tham số thực). Xác định tất cả giá trị của tham số m để A ∩ B = ∅.
Câu 92:
Cho A = 3 + 32 + 33 + … + 399 + 3100. Hỏi 2A + 3 có phải là số chính phương không?
Câu 94:
Cho A = (2m - 1; 2m + 3) và B = (-1; 1).
Xác định m để B là tập con A và A ∩ B = ∅.