189 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 46)
Haylamdo biên soạn và sưu tầm 189 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
189 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 46)
Câu 2:
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng: .
Câu 3:
Cho ABC vuông tại A có AB < AC. Gọi D, E lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của cạnh EF.
a) Chứng minh tứ giác BFCE là hình bình hành.
b) Chứng minh tứ giác BFEA là hình chữ nhật.
c) Gọi K là điểm đối xứng với F qua E. Chứng minh tứ giác AFCK là hình thoi.
d) Vẽ AH ⊥ BC tại H. Gọi M là trung điểm của HC. Chứng minh FM ⊥ AM.
Câu 4:
Câu 6:
Câu 7:
Lúc 8h một người đi xe đạp chuyển động thẳng đều với vận tốc 12km/h gặp một người đi bộ đi ngược chiều chuyển động thẳng đều với vận tốc 4km/h trên cùng một đoạn đường. Lúc 8h30 người đi xe đạp dừng lại nghỉ 30 phút rồi quay lại đuổi theo người đi bộ với vận tốc cũ. Hỏi hai người gặp nhau ở đâu? Lúc nào?
Câu 8:
Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II. Gọi x là số tấn nguyên liệu loại I, y là số tấn nguyên liệu loại II cần dùng. Khi đó hệ điều kiện của x, y để tính số nguyên liệu mỗi loại cần dùng là gì?
Câu 10:
Một thầy giáo có 10 cuốn sách toán đôi 1 khác nhau , trong đó có 3 cuốn đại số, 4 cuốn giải tích và 3 cuốn hình học , Ông muốn lấy ra 5 cuốn và tặng cho 5 học sinh sao cho sau khi tặng mỗi loại sách còn lại ít nhất 1 cuốn . Hỏi có bao nhiêu cách tặng?
Câu 12:
Tìm m để phương trình x3 – 2x2 + (1 – m)x + m = 0 có 3 nghiệm phân biệt x1, x2, x3 thỏa mãn x12 + x22 + x32 = 4.
Câu 13:
Cho tam giác ABC. I nằm trên BC cho 2CI = 3BI. J nằm trên đường thẳng BC cho 5JB = 2JC. G là trọng tâm tam giác ABC.
a) Biểu diễn theo 2 vectơ và biểu diễn qua .
b)Tính theo .
Câu 14:
Cho (O; R) và (O; R') tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O') sao cho AM vuông góc với AN. Chứng minh:
a) OM song song O'N;
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO' lớn nhất.
Câu 15:
Tìm góc α ∈ để phương trình cos2x + sin2x – 2cosx = 0 tương đương với phương trình cos(2x – α) = cosx.
Câu 16:
Tính diện tích hình thang vuông ABCD, biết = 90°, AB = 3cm, AD = 4cm và = 135°.
Câu 17:
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 9cm ; AC=12cm
a) Tính số đo góc B (làm tròn đến độ) và độ dài BH
b) Gọi E, F là hình chiếu của H trên AB, AC. Chứng minh AE.AB = AF.AC.
Câu 18:
Cho tam giác ABC vuông tại A, đường cao AH, biết AB = 9cm, AC = 12cm. Tính BC, AH, HB, HC, diện tích tam giác ABC.
Câu 19:
Lớp 10A chọn ra một số học sinh tham gia làm bài khảo sát học sinh giỏi môn Toán. Đề thi có 3 câu. Sau khi chấm bài giáo viên tổng kết được như sau: Có 5 học sinh làm được câu 1, có 6 học sinh làm được câu 2, có 4 học sinh làm được câu 3. Có 3 học sinh làm được câu 1 và câu 2, có 2 học sinh làm được câu 1 và câu 3, có 1 học sinh làm được câu 2 và câu 3 và chỉ có 1 học sinh làm được cả 3 câu. Hỏi có tất cả bao nhiêu học sinh tham gia làm bài khảo sát?
Câu 20:
Cho biểu thức C =
a) Tìm x để biểu thức C có nghĩa.
b) Rút gọn biểu thức C.
c) Tìm x để giá trị của phân thức C > 0.
Câu 22:
Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
Câu 23:
Từ một điểm A nằm ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Trên cung nhỏ BC lấy một điểm M bất kỳ, vẽ MI vuông góc với AB, MK vuông góc với AC (I thuộc AB, K thuộc AC).
a) Chứng minh AIMK, ABOC là các tứ giác nội tiếp;
b) Vẽ MP vuông góc với BC (P thuộc BC). Chứng minh ;
c) Chứng minh MI.MK = MP2;
d) Xác định vị trí của điểm M trên cung nhỏ BC để tích MI.MK.MP đạt giá trị lớn nhất.
Câu 24:
Cho hình bình hành ABCD . Gọi M, N lần lượt là trung điểm AB, CD . Đường chéo BD cắt AN , CM theo thứ tự ở E và K. Chứng minh:
a) AMCN là hình bình hành.
b) DE = KB.
c) AK đi qua trung điểm của I của BC.
Câu 27:
Cho tam giác ABC có các trung tuyến BD và CE . Trên cạnh BC lấy các điểm M N, sao cho BM = MN = NC. Gọi I là giao điểm của AM và BD , K là giao điểm của AN và CE . Chứng minh rằng:
a) BCDE là hình thang.
b) K là trung điểm của EC.
c) BC = 4IK
Câu 29:
Cho hàm số bậc nhất y = (2m + 1)x + m – 2. Tìm m biết rằng góc tạo bởi đường thẳng và trục Ox bằng 45°.
Câu 30:
Cho góc tù α có sin α = .
a) Tính cos α, tan α, cot α
b) Tính giá trị biểu thức:
A = sinα . cot (180° – α) + cos(180° – α). cot (90° – α)
B = .
Câu 33:
Cho tam giác MNP vuông tại M đường cao MH . Gọi D,F lần lượt là chân các đường vuông góc HA từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm HP. Chứng minh ∆DEA vuông.
c) Tam giác MNP có thêm điều kiện gì để DE = 2EA.
Câu 34:
Một người vay ngân hàng 30 000 000 (ba mươi triệu) đồng với lãi suất ngân hàng là 5% một năm và theo thể thức lãi đơn (tiền lãi không gộp vào chung với vốn). Hãy thiết lập hàm số thể hiện mối liên hệ giữa tổng số tiền nợ T (VNĐ) và số nợ (năm).
Câu 35:
Cho tam giác ABC. Hai điểm M, N được xác định bởi hệ thức: . Tìm mệnh đề đúng trong các mệnh đề sau: (1) MN và AC song song; (2) MN và AC cắt nhau; (3) MN = AC; (4) 3 điểm M, A, C thẳng hàng
Câu 36:
Cho tam giác ABC vuông tại A, có đường cao AH. Từ H kẻ HE vuông góc với AB tại E, HF vuông góc với AC tại F.
a) Cho biết AB = 3cm, = 30°. Tính độ dài các đoạn AC, HA.
b) Chứng minh: BE.BA + CF.CA + 2.HB.HC = BC2.
Câu 37:
Trong mặt phẳng Oxy, cho đường tròn (C'):x² + y –4x+10y+4=0. Viết phương trình đường tròn (C) biết (C') là ảnh của (C) qua phép quay với tâm quay là gốc tọa độ 0 và góc quay bằng 270°.
Câu 38:
Cho bốn điểm A; B; C; D. Gọi I; J lần lượt là trung điểm của các đoạn thẳng AB và CD. Trong các đẳng thức sau, đẳng thức nào sai?
A.
B.
C.
D.
Câu 39:
Cho đường tròn (O,R) cố định. Từ M nằm ngoài đường tròn (O) kẻ 2 tiếp tuyến MA,MB (A,B là các tiếp điểm). Gọi H là giao điểm của OM, AB.
a) Chứng minh: OM vuông góc với AB và OH.OM = R2.
b) Từ M kẻ cát tuyến MNP với đường tròn (O) (N nằm giữa M,P), gọi I là trung điểm NP (I khác O). Chứng minh: A, M, O, I thuộc một đường tròn và tìm tâm của đường tròn đó.
c) Qua N kẻ tiếp tuyến với đường tròn (O), cắt MA, MB theo thứ tự C,D. Biết MA = 5cm, tính chu vi tam giác MCD.
d) Qua O kẻ đường thẳng d vuông góc với OM, cắt MA, MB lần lượt tại E, F. Xác định vị trí của điểm M để diện tích tam giác MEF nhỏ nhất.
Câu 40:
Bảng giá cước gọi quốc tế của công ty viễn thông A được cho bởi bảng sau:
|
Thời gian gọi (phút) |
Giá cước điện thoại (đồng/phút) |
|
Không quá 8 phút |
6 500 |
|
Từ phút thứ 9 đến phút thứ 15 |
6 000 |
|
Từ phút thứ 16 đến phút thứ 25 |
5 500 |
|
Từ phút thứ 26 trở đi |
5 000 |
Gọi T (đồng) là số tiền khách hàng phải trả khi gọi quốc tế trong t phút. Lập hàm số của T theo t.
Câu 41:
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến: (x – 5)(2x + 3) – 2x(x – 3) + x + 7.
Câu 42:
Hình bình hành ABCD có AB = a, BC = a và . Khi đó hình bình hành có diện tích bằng bao nhiêu?
Câu 46:
Trong giải bóng đá nữ ở trường THPT có 12 đội tham gia, trong đó có hai đội của hai lớp 12A2 và 11A6. Ban tổ chức tiến hành bốc thăm ngẫu nhiên để chia thành hai bảng đấu A, B mỗi bảng 6 đội. Xác suất để 2 đội của hai lớp 12A2 và 11A6 ở cùng một bảng là?
Câu 47:
Tổng của 5 số là 600. Tìm số thứ 5, biết rằng số này bằng số trung bình cộng của bốn số còn lại.
Câu 49:
Bạn An mua một số táo và lê. Biết rằng hiệu bình phương của số táo và lê bằng 41. Hỏi bạn An mua bao nhiêu quả táo (Biết rằng số táo nhiều hơn lê)?
Câu 50:
Cho tam giác ABC có độ dài 3 cạnh AB = 14cm ; BC = 12cm ; CA = 10cm . Phân giác trong của cắt BC tại D. Tính độ dài DB; DC và tỉ số diện tích
Câu 51:
Một xe đi nửa đoạn đường đầu tiên với tốc độ trung bình v1 = 12km/h và nửa đoạn đường sau với tốc độ trung bình v2 = 20km/h. Tính tốc độ trung bình trên cả đoạn đường.
Câu 57:
Một khu đất hình chữ nhật có chiều dài là 127m, chiều rộng kém chiều dài 29m. Người ta đóng cọc xung quanh khu đất cứ 5m đóng 1 cọc. Tính số cọc cần để đóng.
Câu 59:
Cho đường tròn (O ; R) và một điểm A sao cho OA = 2R vẽ các tiếp tuyến AB, AC với (O;R) , B và C là các tiếp điểm. Vẽ đường kính BOD.
a) Chứng minh 4 điểm A, B, O, C cùng thuộc một đường tròn.
b) Chứng minh DC // OA.
c) Đường trung trực của BD cắt AC và CD lần lượt tại S và E. Chứng minh OCEA là hình thang cân.
Câu 64:
Một người dự định đi bộ quãng đường với vận tốc 5km/h nhưng khi đi được nửa đường thì nhờ được bạn đèo xe đạp đi tiếp với vận tốc 12km/h do đó đến sớm hơn dự định 28 phút. Hỏi người ấy đi hết toàn bộ quãng đường trong bao lâu?
Câu 67:
Cho đường tròn tâm (O) có đường kính BC. Kẻ tiếp tuyến Bx với nửa đường tròn (O). Trên tia đối của CB lấy điểm A. Kẻ tiếp tuyến AE với nửa đường tròn, tia AE cắt Bx tại D (Bx nằm trên nửa mặt phẳng bờ BC chứa nửa đường tròn (O)).
a) Chứng minh: DO // EC.
b) Chứng minh: AO.AB = AE.AD.
Câu 68:
Một nhà máy sản xuất sản phẩm với 40% sản phẩm loại I, 50% sản phẩm loại II, còn lại là phế phẩm. Lấy ngẫu nhiên 1 sản phẩm của nhà máy. Tính xác suất sản phẩm lấy ra là loại I hoặc loại II?
Câu 69:
Một chiếc thuyền dự định đi từ vị trí A bên bờ sông này đến vị trí B bên bờ sông kia. AB vuông góc với 2 bờ sông. Do dòng nước chảy xiết nên chiếc thuyền đã đi lệch góc so với AB và đến vị trí C bên bờ bên kia. Biết khoảng cách giữa 2 bờ sông là 160 m. Tính thời gian chuyển động của thuyền, biết vận tốc nước chảy so với bờ là 2 m/s.
Câu 70:
Câu 72:
Hai người đi xe từ A đến C. Người thứ nhất đi theo đường từ A đến B rồi từ B đến C. Người thứ hai đi thẳng từ A đến C. Cả hai đều về đích cùng lúc. Tính quãng đường và độ dịch chuyển của người thứ nhất và người thứ hai, so sánh và nhận xét kết quả.
Câu 73:
Tam giác ABC có AC = 4, = 60°. Tính độ dài đường cao h xuất phát từ đỉnh A của tam giác.
Câu 79:
Hiện nay anh hơn em 13 tuổi biết sau 7 năm nữa tuổi anh gấp 2 lần tuổi em. Tìm tuổi em và tuổi anh hiện nay?
Câu 80:
Câu 81:
Cho n là một số nguyên dương bất kỳ và Tn = 15 + 25 + 35 + ... + n5 , An = 1 + 2 + 3 + ... + n. Chứng minh: Tn chia hết An.
Câu 82:
Cho hình bình hành ABCD. Các đường phân giác của các góc lần lượt cắt nhau tại E, F, G, H. Chứng minh: EFGH là hình chữ nhật.
Câu 85:
Có bao nhiêu cách xếp 3 quả bóng giống nhau vào 5 chỗ khác nhau (mỗi chỗ xếp không quá một quả bóng)?
Câu 86:
Cho hình chữ nhật ABCD có AB = 4cm, BC = 3cm. Kẻ BH vuông góc với AC tại H, tia BH cắt AD tại E.
1) Tính BH, góc BAC.
2) Chứng minh: BH.BE = CD2.
Câu 87:
Hai người khách du lịch xuất phát đồng thời từ hai thành phố cách nhau 38 km. Họ đi ngược chiều và gặp nhau sau 4 giờ.Hỏi vận tốc của mỗi người biết rằng đến khi gặp nhau, người thứ nhất đi được nhiều hơn người thứ hai là 2 km.
Câu 88:
Cho tam giác ABC và điểm M thỏa mãn . Trên các cạnh AC, BC lấy các điểm P, Q sao cho CPMQ là hình bình hành. Lấy điểm N trên AQ sao cho (với a, b ∈ ℤ và a, b nguyên tố cùng nhau). Khi ba điểm B, N, P thẳng hàng hãy tính a + b.
Câu 90:
Câu 91:
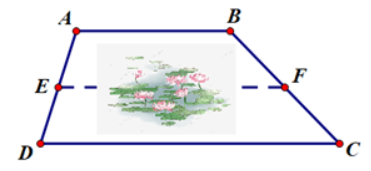
Tại môt khu nghỉ dưỡng người ta muốn xây một cây cầu bắc qua ao sen (đoạn EF để du khách có thể đi bộ ngắm sen và đàn cá KOI bơi, cây cầu đi bộ này song song với hai con đường AB và DC. Em hãy tính độ dài cây cầu EF, biết con đường AB và DC dài lần lượt là 30m và 50m, E và F là điểm chính giữa AD và BC.
Câu 92:
Một bể bơi có chiều dài 25m, chiều rộng 10m và sâu 1,5m. Bể đó đc lát đáy và xung quanh bằng gạch men hình vuông có cạnh 5dm. Tính số gạch dùng để lát bể bơi đó.
Câu 93:
Có bao nhiêu số tự nhiên có chín chữ số mà các chữ số của nó viết theo thứ tự giảm dần?
Câu 94:
Cho tam giác ABC và ba điểm M, N, P thỏa mãn , , . Chứng minh rằng M, N, P thẳng hàng.
Câu 95:
Trên cạnh BC của hình tam giác ABC có các điểm M,N sao cho BM = MN = NC. So sánh diện tích các hình tam giác AMN, AMN, ANC. Tính diện tích mỗi hình tam giác đó, biết diện tích hình tam giác ABC là 77,4m2
Câu 96:
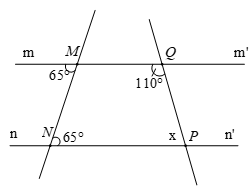
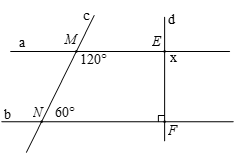
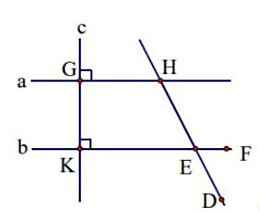
Cho hình vẽ biết
a) Chứng minh a // b.
b) Tính số đo của
c) Vẽ Hx và Ey lần lượt là tia phân giác của và . Chứng minh Hx // Ey.
Câu 97:
Cho tứ giác ABCD có AC = 10cm, BD = 12cm. Góc giữa AC và BD bằng 30 độ. Tính diện tích tứ giác đó.
Câu 98:
Cho biểu thức C =
a) Tìm x để biểu thức C có nghĩa.
b) Rút gọn biểu thức C.
c) Tìm giá trị của x để C = .
d) Tìm x để giá trị của phân thức C > 0.
Câu 99:
Có bao nhiêu cặp số nguyên (x; y) thỏa mãn 0 ≤ x ≤ 2020 và log2(4x + 4) + x = y + 1 + 2y?
Câu 101:
Bác Năm mới mua miếng đất hình vuông có diện tích 3600 m2. Bác tính làm hàng rào bằng dây kẽm gai hết tất cả 5000000 đồng bao gồm cả chi phí dây kẽm và tiền công làm. Gọi x là giá mỗi mét dây kẽm (x > 0), y là số tiền công làm hàng rào.
a) Hãy viết hàm số tính công làm hàng rào.
b) Hỏi bác Năm phải trả bao nhiêu tiền công để thợ rào hết hàng rào. Biết rằng giá mỗi mét dây kẽm là 15.000 đồng.
Câu 102:
Cho tam giác ABC vuông tại A có = 60°. Qua A kẻ đường thẳng d song song với BC. Trên d lấy điểm D sao cho AD = DC.
a) Tính số đo góc BAD .
b) Chứng minh ABCD là hình thang cân.
c) Gọi E là trung điểm của BC, chứng minh ADEB là hình thoi.
Câu 104:
Cho hình tam giác ABC,M là điểm chính giữa cạnh BC. Từ M kẻ MQ và MP vuông góc với các cạnh AC và AB. So sánh diện tích tam giác ABM và AMC. Tính diện tích tam giác ABC biết MQ = 4cm; MP = 6cm và AC – AB = 8cm.
Câu 105:
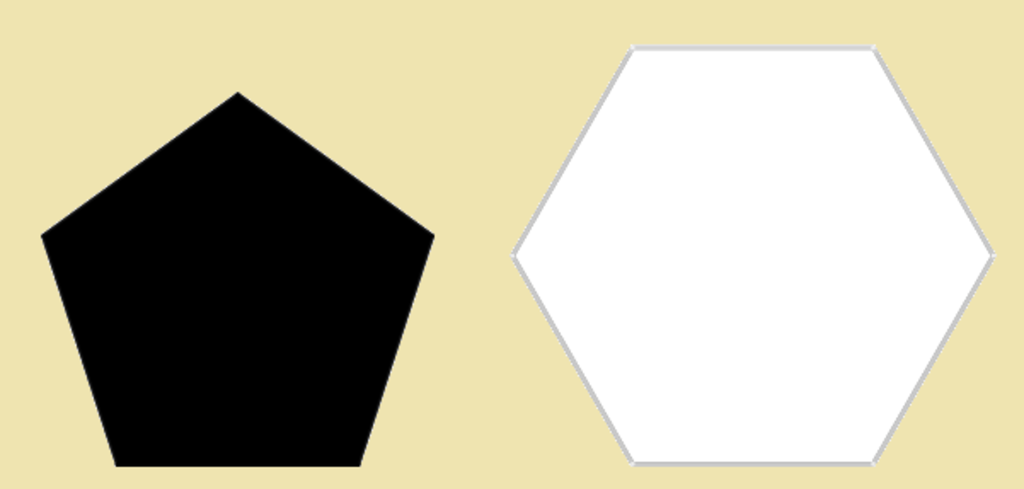
Một quả bóng được khâu từ 32 miếng da gồm hai loại như hình vẽ:
Biết rằng mỗi miếng màu đen chỉ giáp với 5 miếng màu trắng và mỗi miếng màu trắng giáp với 3 miếng màu đen. Hỏi có bao nhiêu miếng da màu trắng?
Câu 107:
Cho hình chóp có S.ABC đáy ABC là tam giác vuông cân, BA = BC = a, , biết khoảng cách từ A đến mặt phẳng (SBC) bằng .
Tính góc giữa SC và mặt phẳng (ABC).
Câu 108:
Cho khối chóp S.ABC có đáy là tam giác vuông tại B , . AB = a , BC = 2a . Biết rằng góc giữa đường thẳng SB và mặt phẳng đáy bằng 60°. Thể tích khối chóp đã cho bằng?
Câu 109:
Cho tam giác ABC (AB < AC), AD là phân giác trong của góc A. Qua trung điểm E của cạnh BC, vẽ đường thẳng song song với AD, cắt cạnh AC tại F, cắt đường thẳng AB tại G. Chứng minh CF = BG.
Câu 113:
Khi đo chiều dài của chiếc bàn học, một học sinh viết được kết quả: C = 118 ± 2 (cm). Sai số tỉ đối phép đo đó bằng?
Câu 115:
Cho tam giác ABC vuông góc tại A có AB = 3, AC = 4. Trên đoạn thẳng BC lấy điểm M sao cho MB = 2MC. Tính tích vô hướng
Câu 117:
Cho đường tròn (O;R) đường kính AB. Vẽ tiếp tuyến Bx của (O). Trên cùng một nửa mặt phẳng bờ AB có chứa Bx, lấy điểm M thuộc (O) (M khác A và B) sao cho MA > MB. Tia AM cắt Bx tại C. Từ C kẻ tiếp tuyến thứ hai CD với (O) (D là tiếp điểm).
1) Chứng minh OC ⊥ BD.
2) Chứng minh bốn điểm O, B, C, D cùng thuộc một đường tròn.
3) Chứng minh .
4) Kẻ MH vuông góc với AB tại H. Tìm vị trí của M để chu vi tam giác OMH đạt giá trị lớn nhất.
Câu 119:
Tại cửa hàng giá niêm yết một cái áo là 300000 đồng. Nếu bán với giá bằng ba phần tư giá niêm yết thì được lãi 20%. Hỏi để lãi 40% thì cửa hàng bán giấ niêm yết là bao nhiêu?
Câu 120:
Cho tam giác ABC nhọn, các đường cao AD,BE,CF cắt nhau tại H.
a) Chứng minh: Tam giác ABE và tam giác AFC đồng dạng, AF. AB = AE . AC.
b) Chứng minh = .
c) Cho AE = 3cm, AB = 6cm. Chứng minh: SABC = 4SAEF.
Câu 121:
Cho tam giác ABC vuông tại A (AB<AC). Gọi D, E lần lượt là trung điểm của BC, AC. Trên tia đối của tia DE lấy điểm F sao cho D là trung điểm của EF. Vẽ AH vuông góc với BC (H thuộc BC). trên đoạn thẳng HC lấy điểm M sao cho HM = MC. Chứng minh AM vuông góc với FM.
Câu 123:
Cho hình vuông ABCD có M là trung điểm AD N thuộc CD sao cho NC = 2ND tính .
Câu 124:
Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Chứng minh OA vuông góc với BC tại H.
b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.AD = AH.AO.
Câu 125:
Một trường có 1030 học sinh. Số học sinh nam chiếm 40%. Tính số học sinh nữ.
Câu 126:
Một hộp đựng 8 bi trắng, 7 bi đỏ và 5 bi xanh. Chọn ngẫu nhiên có hoàn lại từng bi cho tới khi lấy được đến bi xanh thứ hai thì ngừng lại. Tính xác suất để chọn được đúng 3 bi trắng, 2 bi đỏ trước khi ngừng.
Câu 129:
Cho tam giác ABC có diện tích là 480cm2. M là trung điểm của cạnh BC. N là trung điểm của AM. Nối BN và kéo dài cắt AC tại I.
a) Tính diện tích tam giác BNM.
b) So sánh AI và IC.
Câu 131:
Cho nửa đường tròn tâm O đường kính AB =2R và điểm M nằm trên đường tròn đó (M ≠ A, B) tiếp tuyến tại điểm M của nửa đường tròn tâm O cắt các tiếp tuyến tại A và B. Lần lượt tại các điểm C, D. Gọi E là giao điểm của OC với AM, gọi F là giao điểm của OD và BM.
a) Chứng minh CD = AC + BD.
b) Chứng minh EF vuông góc BD và EF là tiếp tuyến đường tròn đi qua các điểm M, D, F.
Câu 132:
Cho đường tròn tâm O, điểm M bất kỳ bên ngoài đường tròn. Vẽ các tiếp tuyến MA và MB với đường tròn. Vẽ đường kính AC. Chứng minh 4 điểm A, B, C, O cùng nằm trên 1 tam giác vuông.
Câu 133:
Chứng minh giá trị của biểu thức sau không phụ thuộc vào biến x.
A = x(3x2 – x + 5) – (2x3 + 3x – 25) – x(x2 – x + 2).
B = x(2x + 1) – x2(x + 2) + (x3 – x + 10).
Câu 135:
Cho tam giác ABC (AB < AC), đường cao AK. Vẽ đường tròn tâm O đường kính BC. Từ A kẻ các tiếp tuyến AM, AN với đường tròn (O) (M, N là các tiếp điểm; M và B nằm trên nửa mặt phẳng có bờ là đường thẳng AO). Gọi H là giao điểm của hai đường thẳng MN và AK. Chứng minh rằng:
a) Tứ giác AMKO nội tiếp đường tròn.
b) KA là tia phân giác của .
c) AN2 = AK.AH.
d) H là trực tâm của tam giác ABC.
Câu 137:
Cho hàm số bậc nhất y = m – 1 + (m + 2)x. Tìm tọa độ điểm cố định mà đường thẳng y luôn đi qua.
Câu 138:
Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại D.
a) Chứng minh tam giác ABD bằng tam giác ADC.
b) Kẻ DH vuông góc với AB (H thuộc AB), DK vuông góc với AC (K thuộc AC). Chứng minh DH = CK.
c) Biết = 4 , tính số đo các góc của tam giác ABC.
Câu 139:
Cho tứ diện ABCD. Gọi P, Q lần lượt là trung điểm của các cạnh BC, AD. Giả sử AB = CD = a và PQ = . Tìm số đo góc giữa hai đường thẳng AB và CD.
Câu 142:
Cho nửa đường tròn tâm O đường kính AB và M là điểm nằm trên (O). Tiếp tuyến tại M cắt tiếp tuyến tại A và B của (O) lần lượt ở C và D. Đường thẳng AM cắt OC tại E, đường thẳng BM cắt OD tại F
a, Chứng minh: = 90°.
b, Tứ giác MEOF là hình gì?
c, Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
Câu 144:
Có 3 học sinh nữ và 2 học sinh nam. Ta muốn sắp xếp vào 1 bàn dài có 5 ghế ngồi. Hỏi có bao nhiêu cách xếp cho 3 học sinh nữ ngồi liền nhau.
Câu 146:
Một người đi xe máy từ A đến B. Cùng lúc đó, một người khác cũng đi xe máy từ B đến A với vận tốc bằng 4:5 vận tốc của người đi từ A đến B. Sau 2 giờ, hai người gặp nhau Hỏi mỗi người đi quãng đường AB hết bao lâu?
Câu 150:
Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng nhau” và Q: “Nếu 17 là số chẵn thì 25 là số chính phương”. Xét tính đúng, sai của mệnh đề P và Q?
Câu 154:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên cạnh SA sao cho MA = 2MS.
a) Chứng minh OM // (SCD).
b) Xác định giao điểm N của MD và mặt phẳng (SBC).
Câu 155:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông bằng cạnh bằng a, tam giác SAB là tam giác đều, SC = SD = . Tính thể tích V của khối chóp S.ABCD?
Câu 157:
Cho tam giác ABC có hai trung tuyến BD và CE cắt nhau tại G. Gọi M ,N theo thứ tự là trung điểm của BG và CG.
a, Chứng minh tứ giác MNDE là hình bình hành .
b, Tìm điều kiện của tam giác ABC để MNDE là hình chữ nhật.
Câu 158:
Cho tam giác ABC có đường cao AD, và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC, AC. Chứng minh
a) Bốn điểm E, F, I, K cùng thuộc một đường tròn.
b) Điểm D cũng thuộc đường tròn đi qua bốn điểm E, F, I, K.
Câu 159:
Cho tam giác ABC, N là điểm xác định bởi , G là trọng tâm tam giác ABC. Hệ thức tính theo và là?
Câu 160:
Cho tập hợp A={1;2;3;...;n} trong đó n là số nguyên dương lớn hơn 1. Hỏi có bao nhiêu cặp sắp thứ tự (x;y) thõa mãn: x và y thuộc A; x lớn hơn y?
Câu 162:
Có bao nhiêu tập hợp X thỏa mãn điều kiện {0; 1; a} hợp với X = {0; 1; a; b; c}.
Câu 163:
Một mảnh đất hình chữ nhật có chu vi 180m, chiều dài hơn chiều rộng 22m.
a) Tính chiều dài và chiều rộng của mảnh đất đó.
b) Tính diện tích của mảnh đất đó.
Câu 164:
Một hình tam giác có diện tích là 8m2 và độ dài cạnh đáy là 32dm. Tìm chiều cao của hình tam giác tương ứng với cạnh đáy đó.
Câu 165:
Một hộp chứa 6 viên bi đỏ và 4 viên bi xanh. Lấy lần lượt 2 viên bi từ hộp đó. Xác suất để viên bi được lấy lần thứ 2 là bi xanh bằng bao nhiêu?
Câu 166:
Một xí nghiệp đóng giày dự định hoàn thành kế hoạch trong 26 ngày. Nhưng do cải tiến kĩ thuật nên mỗi ngày đã vượt mức 6000 đôi giày, do đó chẳng những đã hoàn thành kế hoạch đã định trong 24 ngày mà còn vượt mức 104000 đôi giày. Tính số đôi giày phải làm theo kế hoạch?
Câu 167:
Tìm phân số tối giản nhỏ nhất (với > 0) biết khi chia cho và được thương là các số nguyên.
Câu 168:
Tại cửa hàng bán hoa giá bán ban đầu của một bó hoa là 60 000 đồng. Vào ngày quốc tế phụ nữ 8/3, giá mỗi bó được giảm 20% và nếu khách mua 10 bó trở lên thì từ bó thứ 10 trở đi khách hàng sẽ chỉ trả một nửa giá đang bán. Một vị khách mua hoa đã trả 648 000 đồng. Hỏi khách này đã mua bao nhiêu bó hoa ?
Câu 171:
Cho hàm số y = (m–1)x + m – 4 (m là tham số và m khác 1).
a) Tìm giá trị của m để đồ thị hàm số đi qua điểm A(2; 3).
b) Vẽ đồ thị hàm số với giá trị của m tìm được ở phần a.
c) Tìm m biết đồ thị hàm số cắt đường thẳng y = 3x + 2 tại điểm có hoành độ là –2.
Câu 172:
Để sản xuất một tờ giấy A5 lần 5 lít nước. Một cuốn sổ A5 có 300 trang. Hỏi để sản xuất ra cuốn sổ đó cần bao nhiêu mét khối nước?
Câu 176:
Một bồn hoa có dạng hình vuoong có độ dài cạnh là 2m . Để làm lối đi rộng hơn, người ta thu nhỏ bồn hoa vẫn có dạng hình vuông nhưng độ dài cạnh giảm đi 50cm .
a) Tính diện tích bồn hoa sau khi thu nhỏ.
b) Lối đi được tăng thêm bao nhiêu diện tích?
Câu 179:
B. y =
C. x = 3y
Câu 180:
Công thức nào sau đây cho ta quan hệ với tỉ lệ thuận?
B. y = 2x – 1
C. y =
D. y = –2x2
Câu 182:
Cho a, b là các số tự nhiên khác 0. Biết 1 > .
Tìm giá trị lớn nhất của A = .
Câu 183:
Tam giác ABC. Gọi D, E, F lần lượt là trung điểm của cạnh AB, AC, BC và M, N, P, Q theo thức tự là trung điểm của đoạn thẳng DA, AE, EF, FD
a. Chứng minh: EF là đường trung bình của tam giác ABC.
b. Chứng minh: Tứ giác DAEF, MNPQ là hình bình hành.
c. Khi tam giác ABC vuông tại A thì các tứ giác DAEF, MNPQ là hình gì?
d. Tìm điều kiện của tam giác ABC để tứ giác MNPQ là hình vuông
Câu 184:
Cho tam giác ABC có BD, CE là các trung tuyến cắt nhau tại G.
a) Tứ giác BEDC hình gì ?
b) Gọi M, N lần lượt là trung điểm của BG và CG. Chứng minh tứ giác MEDN là hình bình hành.
c) Tam giác ABC có thêm điều kiện gì thì tứ giác MEDN là hình chữ nhật.
Câu 185:
Xét tất cả các số thực x, y sao cho đúng với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x2 + y2 + x – 3y bằng:
Câu 186:
Ba ban Lâm, Chí, Dũng có 60 cây bút và số bút tỉ lệ với 3, 4, 5. Tính số bút của mỗi bạn.
Câu 188:
Bán kính của một bánh xe ô tô là 0,25m. Tính chu vi bánh xe đó. Nếu ô tô đó đi hết quãng đường dài 4,71km thì bánh xe lăn trên mặt đất được bao nhiêu vòng?
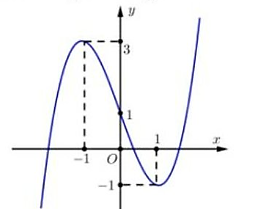
Câu 189:
Cho hàm số y = f(x) xác định trên tập hợp R và có đồ thị như hình vẽ bên dưới. Hàm số y = f(2 – x) nghịch biến trên khoảng nào?