69 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 42)
Haylamdo biên soạn và sưu tầm 69 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
69 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 42)
Câu 4:
Cho hình vuông ABCD.Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE=CF. Chứng minh tam giác EDF vuông cân.
Câu 5:
Cho hình vuông ABCD.Trên tia đối của tia BA lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho AE = CF. Gọi I là trung điểm của EF. Chứng minh BI = DI.
Câu 8:
Cho hình chóp tam giác đều S.ABC có các cạnh bên SA, SB, SC vuông góc với nhau từng đôi một. Biết thể tích của khối chóp bằng . Tính bán kính r của mặt cầu nội tiếp của hình chóp S.ABC.
Câu 9:
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD và AB = 2CD). Gọi M là trung điểm của cạnh SC. Xác định giao điểm K của đường thẳng AM với (SBD).
Câu 10:
Cho (S) là một mặt cầu cố định có bán kính R. Một hình trụ (H) thay đổi nhưng luôn có hai đường tròn đáy nằm trên (S). Gọi V1 là thể tích của khối cầu (S) và V2 là thể tích lớn nhất của khối trụ (H). Tính tỉ số .
Câu 11:
Cho tam giác ABC vuông cân tại A. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh A là trung điểm của CI.
Câu 12:
Cho tam giác ABC vuông tại A, AB = AC. Trên các cạnh AB, AC lấy tương ứng hai điểm D, E sao cho AD = AE. Từ A và D kẻ đường vuông góc với BE và cắt BC tại M, N. Tia ND cắt tia CA ở I. Chứng minh MC = MN.
Câu 13:
Một cửa hàng sách hạ giá 10% giá sách nhân ngày Quốc tế thiếu nhi ngày 1/6. Tuy vậy, cửa hàng vẫn còn lãi 8%. Hỏi ngày thường thì cửa hàng được lãi bao nhiêu phần trăm?
Câu 14:
Sau khi giảm giá 20% thì giá của một quyển sách là 9 600 đồng. Hỏi lúc đầu gái của quyển sách là bao nhiêu tiền?
Câu 15:
Gọi S là tập hợp các số tự nhiên có hai chữ số. Chọn ngẫu nhiên đồng thời hai số từ tập hợp S. Tính xác suất để hai số được chọn có chữ số hàng đơn vị giống nhau.
Câu 16:
Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hoá, 6 học sinh giỏi Toán và Lý, 5 học sinh giỏi Hoá và Lý, 4 học sinh giỏi Toán và Hoá, 3 học sinh giỏi cà 3 môn. Hỏi số học sinh giỏi ít nhất 1 môn trong 3 môn là bao nhiêu em?
Câu 17:
Có 40 học sinh giỏi, mỗi em giỏi ít nhất 1 môn. Có 22 em giỏi Văn, 25 em giỏi Toán, 20 em giỏi Anh. Có 8 em giỏi đúng hai môn Văn, Toán. Có 7 em giỏi đúng hai môn Toán, Anh. Có 6 em giỏi đúng hai môn Anh, Văn. Hỏi có bao nhiêu em giỏi cả ba môn Văn, Toán, Anh?
Câu 20:
Trong mặt phẳng với hệ tọa độ Oxy, phép quay tâm I góc quay I(4; –3) biến đường thẳng d: x + y – 5 = 0 thành đường thẳng d' có phương trình là bao nhiêu?
Câu 24:
Việt và Nam chơi cờ. Trong một ván cờ, xác suất Việt thắng Nam là 0,3 và Nam thắng Việt là 0,4. Hai bạn dừng chơi khi có người thắng, người thua. Tính xác suất để hai bạn dừng chơi sau 2 ván cờ.
Câu 25:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy và SA = 2a. Gọi M là trung điểm của SD. Tính khoảng cách d giữa đường thẳng SB và mặt phẳng (ACM).
Câu 26:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA = a và SA vuông góc với đáy. Tính khoảng cách d giữa hai đường chéo nhau SC và BD.
Câu 28:
Cho hàm số với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng (2; +∞). Tìm số phần tử của S.
Câu 29:
Có bao nhiêu số tự nhiên có 5 chữ số trong đó các chữ số cách đều chữ số đứng giữa thì giống nhau?
Câu 30:
Có 6 quả cầu xanh đánh số từ 1 đến 6, 5 quả cầu đỏ đánh số từ 1 đến 5 và 7 quả màu vàng đánh số từ 1 đến 7. Hỏi có bao nhiêu cách lấy ra 3 quả cầu vừa khác màu vừa khác số?
Câu 31:
Câu 38:
Cho hàm số y = ax4 + bx2 + c (a ≠ 0) có bảng biến thiên dưới đây:
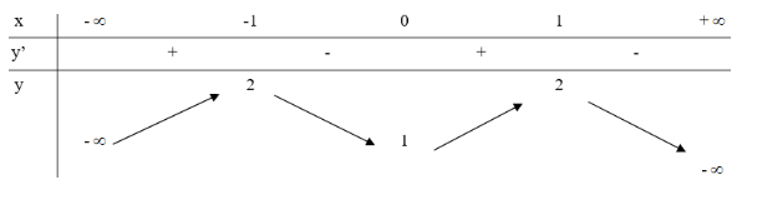
Tính P = a – 2ab + 3c.
Câu 39:
Cho các hàm số: y = 2x − 2 và y = (m + 1)x − m2 – m (m ≠ −1). Tìm m để đồ thị hai hàm số trên là các đường thẳng song song.
Câu 40:
Tìm m để hai đường thẳng (d): y = 3x + 1 và (d′): y = (m−1)x − 2m song song với nhau.
Câu 43:
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
Câu 45:
Một hình thang cân có đường chéo vuông góc với cạnh bên. Biết rằng đáy nhỏ dài 14 cm, đáy lớn dài 50 cm. Tính diện tích hình thang.
Câu 46:
Cho hàm số y = –x3 + 3x + 2. Tìm hai điểm trên đồ thị hàm số sao cho chúng đối xứng nhau qua điểm M(–1; 3).
Câu 47:
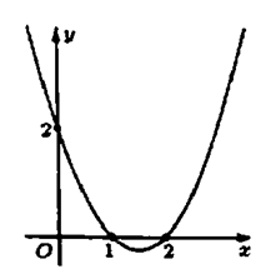
Cho hàm số y = f(x) liên tục trên đoạn [-2;4] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–2; 4]. Tính giá trị của M2 + m2.
![Cho hàm số y = f(x) liên tục trên đoạn [-2;4] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [–2; 4]. Tính giá trị của M2 + m2. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/08/blobid36-1690992556.png)
Câu 50:
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 − 3(m + 2)x2 + 3(m2 + 4m)x + 1 nghịch biến trên khoảng (0; 1).
Câu 51:
Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a; CD = a. Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60º. Gọi I là trung điểm của AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.
Câu 52:
Cho hàm số y = x3 − 3mx2 + 2 có đồ thị (Cm) và đường thẳng Δ: y = −x + 2. Biết (Cm) có hai cực trị và khoảng cách từ điểm cực tiểu của (Cm) đến đường thẳng Δ bằng . Tìm m.
Câu 53:
Cho hàm số y = x3 + 3x2 + mx + m – 2 (m là tham số) có đồ thị là (Cm).
Xác định m để (Cm) có các điểm cực đại và cực tiểu nằm về hai phía đối với trục hoành.
Câu 54:
Cho tứ giác ABCD, O là giao điểm của hai đường chéo AC và BD. Gọi G; G’ theo thứ tự là trọng tâm của tam giác OAB và OCD. Biểu diễn vecto .
Câu 55:
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Câu 56:
Trong mặt phẳng tọa độ Oxy cho hai đồ thị hàm số y = x – 5m và y’ = 3x – m2. Tìm m để 2 đường thẳng cắt nhau tại 1 điểm có hoành độ bằng –3.
Câu 57:
Trong mặt phẳng tọa độ Oxy cho hàm số bậc nhất y = (2k – 1)x + 3 – k (k là hệ số) có đồ thị là đường thẳng (d). Tìm giá trị của k để đồ thị hàm số song song với đường thẳng (m): y = 0,5x – 3.
Câu 58:
Cho hình thang ABCD có hai cạnh đáy là AB và CD mà AB = 3CD. Tìm tỉ số của phép vị tự biến điểm A thành điểm C và biến điểm B thành điểm D.
Câu 61:
Cho hàm số y = f(x) có đạo hàm f '(x) trên R. Hình vẽ bên là đồ thị của hàm số y = f '(x). Hàm số g(x) = f(x − x2) nghịch biến trên khoảng nào trong các khoảng dưới đây:
A. ;
B. ;
C. ;
D. .
Câu 62:
Cho hàm số y = f(x) có bảng biến thiên như hình dưới:
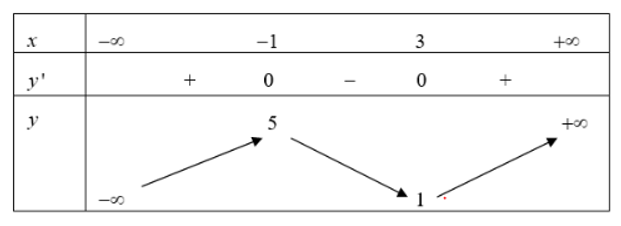
Tìm số điểm cực trị của hàm số y = f(x2 − 4x + 1).
Câu 63:
Từ một đỉnh tháp chiều cao CD = 80 m, người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 72º12’ và 34º26’. Ba điểm A, B, D thẳng hàng. Tính khoảng cách AB?
Câu 64:
Trong kì thi học sinh giỏi tỉnh có 4 bạn Phương, Dương, Hiếu, Hằng tham gia. Được hỏi quê mỗi người ở đâu ta nhận được các câu trả lời sau:
Phương: Dương ở Thăng Long còn tôi ở Quang Trung.
Dương : Tôi cũng ở Quang Trung còn Hiếu ở Thăng Long.
Hiếu : Không, tôi ở Phúc Thành còn Hằng ở Hiệp Hoà.
Hằng : Trong các câu trả lời trên đều có 1 phần đúng 1 phần sai.
Hỏi quê của Dương ở đâu?
Câu 65:
Cho parabol (P): y = x2 và hai điểm A(0; 1); B(1; 3). Viết phương trình đường thẳng AB.
Câu 66:
Cho parabol (P): y = x2 và hai điểm A(0; 1); B(1; 3). Viết phương trình đường thẳng d song song với AB và tiếp xúc với (P).
Câu 67:
Tìm tập hợp tất cả các giá trị của tham số m để hàm số:
y = x3 − mx2 − (m − 6)x + 1 đồng biến trên (0; 4).
Câu 69:
Biết đường thẳng y = x − 2 cắt đồ thị tại hai điểm phân biệt A, B, có hoành độ lần lượt xA; xB. Tính xA + xB .

