48 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 75)

Hệ số góc của tiếp tuyến của đồ thị hàm số \[y = \frac{{{x^4}}}{4} + \frac{{{x^2}}}{2} - 1\] tại điểm có hoành độ x =  ‒1 là:

A. 0

B. 2

C. ‒2

D. 3

Tìm hai số tự nhiên, biết rằng tổng của chúng bằng 2030 và hiệu của số lớn và số bé bằng 30.

Cho đường tròn (C): x² + y² ‒ 2x + 2y ‒ 7 = 0 và đường thẳng d: x + y + 1 = 0. Tìm tất cả các đường thẳng song song với đường thẳng d và cắt đường tròn (C) theo dây cung có độ dài bằng 2.

A. x + y + 4 = 0 và x + y − 4 = 0.

B. x + y + 2 = 0.

C. x + y + 4 = 0.

D. x + y + 2 = 0 và x + y − 2 = 0.

Cho hai đường thẳng d₁ và d₂ song song có bao nhiêu phép tịnh tiến biến đường thẳng d₁ thành đường thẳng d₂:

A. Không có phép tịnh tiến nào.

B. Có duy nhất 1 phép tịnh tiến.

C. Có 2 phép tịnh tiến.

D. Có vô số phép tịnh tiến.

Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy lớn CD. Gọi M là trung điểm của cạnh SA, N là giao điểm của cạnh SB và mặt phẳng (MCD). Mệnh đề nào sau đây là mệnh đề đúng?

A. MN và SD cắt nhau.

B. MN // CD.

C. MN và SC cắt nhau.

D. MN và CD chéo nhau.

Cho hình hộp ABCD.A'B'C'D', gọi M là trung điểm CD, (P) là mặt phẳng đi qua M và song song với B'D và CD'. Thiết diện của hình hộp cắt bởi mặt phẳng (P) là hình gì?

A. Ngũ giác.

B. Tứ giác.      

C. Tam giác.    

D. Lục giác.

Cho lục giác đều ABCDEF tâm O. Các vec tơ đối của vecto \[\overrightarrow {OD} \] là:

A. \[\overrightarrow {OA} ,\overrightarrow {DO} ,\overrightarrow {EF} ,\overrightarrow {CB} .\]

B. \[\overrightarrow {OA} ,\overrightarrow {DO} ,\overrightarrow {EF} ,\overrightarrow {OB} ,\overrightarrow {DA} .\]

C. \[\overrightarrow {OA} ,\overrightarrow {DO} ,\overrightarrow {EF} ,\overrightarrow {CB} ,\overrightarrow {DA} .\]

D. \[\overrightarrow {DO} ,\overrightarrow {EF} ,\overrightarrow {CB} ,\overrightarrow {BC} .\]

Với \[\overrightarrow {DE} \] (khác vec tơ – không) thì độ dài đoạn ED được gọi là:

A. Phương của \[\overrightarrow {ED} \].

B. Hướng của \[\overrightarrow {ED} \].

C. Giá của \[\overrightarrow {ED} \].

D. Độ dài của \[\overrightarrow {ED} \].

Phương trình \[\left| {x - 2} \right|\left( {x + 1} \right) + m = 0\] có ba nghiệm phân biệt, giá trị thích hợp của tham số m là:

A. \[0 < m < \frac{9}{4}.\]

B. 1 < m < 2.

C. \[ - \frac{9}{4} < m < 0.\]

D. ‒2 < m < 1.

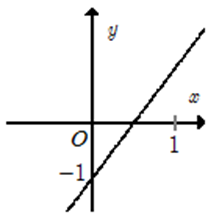
Cho hàm số \[y = \frac{{x + b}}{{cx - 1}}\] có đồ thị như hình bên.  Mệnh đề nào dưới đây đúng?

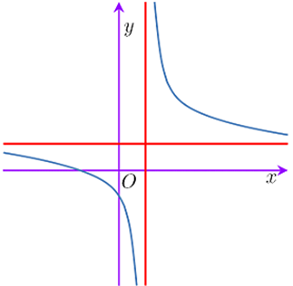
A. c < 0; b < 0.

B. c > 0; b < 0.

C. c < 0; b > 0.

D. c > 0; b > 0.

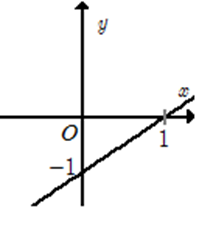
Đồ thị hàm số \[y = \frac{{ax + 2}}{{cx + b}}\] như hình vẽ bên. Chọn khẳng định đúng?

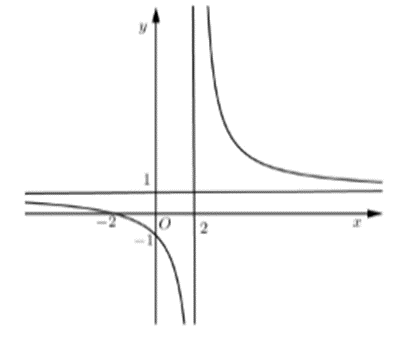
A. a = 2.

B. b = 1.

C. b = 2.

D. c = 1.

Cho khối hộp chữ nhật ABCD.A’B’C’D’ có AA’=a,AB=3a,AC=5a. Thể tích của khối hộp đã cho là:

A. 5a³.

B. 4a³.

C. 12a³.

D. 15a³.

Sắp xếp 5 học sinh lớp A và 5 học sinh lớp B vào hai dãy ghế đối diện nhau, mỗi dãy 5 ghế sao cho 2 học sinh ngồi đối diện nhau thì khác lớp. Khi đó số cách xếp là:

A. 460000.

B. 460500.

C. 460800.

D. 460900.

Cho hai hàm số \(y = \frac{{x - 3}}{{x - 2}} + \frac{{x - 2}}{{x - 1}} + \frac{{x - 1}}{x} + \frac{x}{{x + 1}}\)và y =|x+2|−x + m (m là tham số thực) có đồ thị lần lượt là (C1) và (C2). Tập hợp tất cả các giá trị của m để (C1) và (C2) cắt nhau tại đúng bốn điểm phân biệt là:

A. (−∞; 2].

B. [2; +∞).

C. (−∞; 2).

D. (2; +∞).

Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \[\widehat {BAD} = 60^\circ ,\] SA = a và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng (SCD) bằng:

A. \(\frac{{\sqrt {21} a}}{7}\)

B. \(\frac{{\sqrt {15} a}}{7}\)

C. \(\frac{{\sqrt {21} a}}{3}\)

D. \(\frac{{\sqrt {15} a}}{3}\)

Cho hình chóp S.ABC có đáy là tam giác ABC thỏa mãn AB = AC = 4, \[\widehat {BAC} = 30^\circ \]. Mặt phẳng (P) song song với (ABC) cắt đoạn SA tại M sao cho SM = 2MA. Diện tích thiết diện của (P) và hình chóp S.ABC bằng bao nhiêu?

A. \(\frac{{16}}{9}.\)

B. \(\frac{{14}}{9}.\)

C. \(\frac{{25}}{9}.\)

D. 1.

Cho tam giác ABC. Gọi M là điểm được xác định: \(4\overrightarrow {BM} - 3\overrightarrow {BC} = \vec 0\). Khi đó vectơ \(\overrightarrow {AM} \) bằng

A. \(\overrightarrow {AB} + \overrightarrow {AC} .\)

B. \(\frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\)

C. \(\overrightarrow {\frac{1}{3}AB} + \frac{2}{3}\overrightarrow {AC} .\)

D. \(\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} .\)

Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?

А. \(\overrightarrow {HA} = \overrightarrow {CD} \) và \(\overrightarrow {AD} = \overrightarrow {CH} .\)

B. \(\overrightarrow {HA} = \overrightarrow {CD} \) và \(\overrightarrow {AD} = \overrightarrow {HC} .\)

C. \(\overrightarrow {HA} = \overrightarrow {CD} \) và \(\overrightarrow {AC} = \overrightarrow {CH} .\)

D. \(\overrightarrow {HA} = \overrightarrow {CD} \) và \(\overrightarrow {AD} = \overrightarrow {HC} \) và \(\overrightarrow {OB} = \overrightarrow {OD} .\)

Trong mặt phẳng tọa độ Oxy cho đường thẳng d có phương trình 2x ‒ y + 1 = 0. Để phép tịnh tiến theo vectơ \[\overrightarrow v \] biến d thành chính nó thì vectơ \[\overrightarrow v \] phải là vectơ nào trong các vectơ sau?

A. \[\overrightarrow v = \left( {2;1} \right)\]

B. \[\overrightarrow v = \left( {2; - 1} \right).\]

C. \[\overrightarrow v = \left( {1;2} \right).\]

D. \[\overrightarrow v = \left( { - 1;2} \right).\]

Elip (E) \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) có tâm sai bằng bao nhiêu?

A. \(\frac{4}{5}.\)

B. \(\frac{5}{4}.\)

C. \(\frac{5}{3}.\)

D. \(\frac{3}{5}.\)

Giá trị nhỏ nhất F_min  của biểu thức F(x; y) = y – x trên miền xác định bởi hệ \[\left\{ \begin{array}{l}y - 2x \le 2\\2y - x \ge 4\\x + y \le 5\end{array} \right.\]

A. F_min = 1.

B. F_min = 2.

C. F_min = 3.

D. F_min = 4.

Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình m²(x⁴ ‒ 1) + m(x² ‒ 1) ‒ 6(x ‒ 1) ≥ 0 đúng với mọi x ∈ ℝ. Tổng giá trị của tất cả các phần tử thuộc S bằng:

A. \( - \frac{3}{2}.\)

B. 1.

C. \( - \frac{1}{2}.\)

D. \(\frac{1}{2}.\)

Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3)

A. \[\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{9} = 1.\]

B. \[\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1.\]

C. \[\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1.\]

D. \[\frac{{{x^2}}}{4} + \frac{{{y^2}}}{3} = 1.\]

Số mặt phẳng đối xứng của hình hộp chữ nhật (các kích thước khác nhau) là:

A. 3.

B. 6.

C. 4.

D. 9.

Cho đoạn thẳng AB có độ dài 3 cm và Điểm I, đoạn thẳng A’B’ đối xứng với AB qua I khi đó độ dài của A’B’ là:

A. 3cm.

B. 6cm.

C. 9cm.

D. 12cm

Một người gửi tiết kiệm với lãi suất 6,5% năm và lãi hàng năm được nhập vào vốn. Hỏi khoảng bao nhiêu năm người đó thu được gấp đôi số tiền ban đầu?

A. 11 năm.

B. 9 năm.

C. 8 năm.

D. 12 năm.

A. \[x = - \frac{\pi }{2} + k2\pi .\]

B. \[x = \frac{\pi }{2} + k\pi .\]

C. \[x = k\pi .\]

D. \[x = \frac{\pi }{2} + k2\pi .\]

Biết \[\sin a + \cos a = \sqrt 2 \]. Hỏi giá trị của sin⁴a + cos⁴a bằng bao nhiêu ?

A. \[\frac{3}{2}.\]

B. \[\frac{1}{2}.\]

C. ‒1.

D. 0.

Trong mặt phẳng Oxy cho điểm M(‒2; 5), phép vị tự tâm O tỉ số 2 biến M thành điểm nào sau đây :

A. \[D\left( {1; - \frac{5}{2}} \right).\]

B. D(‒4; 10).

C. D (4; ‒10).

D. \[D\left( { - 1;\frac{5}{2}} \right).\]

Trong mặt phẳng Oxy cho điểm M(‒2; 4). Phép vị tự tâm O tỉ số k = ‒2 biến điểm M thành điểm nào trong các điểm sau?

A. (‒3; 4).

B. (‒4; ‒8).

C. (4; ‒8).

D. (4; 8).

Trong mặt phẳng Oxy, cho điểm M (‒2; 1). Tìm tọa độ điểm N sao cho M là ảnh của N qua phép tịnh tiến theo vectơ v = (‒3; 2) là:

Trong mặt phẳng Oxy, cho các điểm A(3; 5). Tìm ảnh của điểm A qua phép Quay tâm O góc quay 180°

A. A’(‒3; ‒5).

B. A’(3; ‒5).

C. A’(‒3; 5).

D. A’(‒5; ‒3).

Cho hàm số y = 3x⁴ − 2mx² + 2m + m⁴. Tìm tất cả các giá trị của m để đồ thị hàm số đã cho có ba điểm cực trị tạo thành tam giác có diện tích bằng 3.

A. m = ‒3.

B. m = 3.

C. m = 4.

D. m = ‒4.

Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x⁴ ‒ 2mx² có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

A. m > 0.

B. m < 1.

C. \[0 < m < \sqrt[3]{4}.\]

D. 0< m < 1.

Tìm côsin góc giữa 2 đường thẳng d₁: x + 2y ‒ 7= 0 và d₂: 2x ‒ 4y+ 9= 0.

A. \[ - \frac{3}{5}.\]

B. \[\frac{2}{{\sqrt 5 }}.\]

C. \[\frac{1}{5}.\]

D. \[\frac{3}{{\sqrt 5 }}.\]

yếu tố nào sau đây xác định một mặt phẳng

A. Hai đường thẳng cắt nhau.

B. Ba điểm phân biệt.

C. Bốn điểm phân biệt.

D. Một điểm và một đường thẳng.

Hàm số y = 2x ‒ 1 có đồ thị là hình nào trong bốn hình sau?

Trong mặt phẳng Oxy cho hai đường thẳng a: 2x + y + 5 = 0 và b: x ‒ 2y ‒ 3 = 0). Nếu có một phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc đó có thể là góc nào trong các góc cho dưới đây:

A. 45°.

B. 90°.

C. 120°.

D. 60°.

Trong mặt phẳng Oxy cho đường thẳng (d: 2x ‒ y + 1 = 0 ). Để phép quay tâm I góc quay (2017π) biến d thành chính nó thì tọa độ của I là:

A. (2; 1).

B. (2; ‒1).

C. (1; 0).

D. (0; 1).

Cho hình bình hành ABCD, I là giao điểm hai đường chéo. Khi đó, khẳng định nào sau đây là đúng?

А. \(\overrightarrow {AB} - \overrightarrow {IA} = \overrightarrow {BI} .\)

B. \(\overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {DB} = \vec 0.\)

C. \(\overrightarrow {AB} - \overrightarrow {CD} = \vec 0.\)

D. \(\overrightarrow {AC} - \overrightarrow {BD} = \vec 0.\)

Có bao nhiêu cách xếp (5 ) học sinh thành một hàng dọc?

A. 1.

B. 25.

C. 5.

D. 120.

Xét phép vị tự V_(I,3) biến tam giác ABC thành tam giác A'B'C'. Hỏi chu vi tam giác A'B'C' gấp mấy lần chu vi tam giác ABC.

A. 1.

B. 2.

C. 3.

D. 6.

Trong mặt phẳng tọa độ Oxy cho hai đường thẳng a và b có phương trình lần lượt là 4x + 3y + 5 = 0 và x + 7y ‒ 4 = 0. Nếu có phép quay biến đường thẳng này thành đường thẳng kia thì số đo của góc quay φ (0 ≤ φ ≤ 180°) là:

A. 45°.

B. 60°.

C. 90°.

D. 120°.

Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác đều cạnh a. Khoảng cách từ tâm O của tam giác ABC đến mặt phẳng (A'BC) bằng \[\frac{a}{6}\]Thể tích khối lăng trụ bằng

Mệnh đề nào đúng?

A. \(\frac{{3{a^3}\sqrt 2 }}{4}.\)

B. \(\frac{{3{a^3}\sqrt 2 }}{8}.\)

C. \(\frac{{3{a^3}\sqrt 2 }}{{28}}.\)

D. \(\frac{{3{a^3}\sqrt 2 }}{{16}}.\)

Cho lục giác đều ABCDEF có tâm O. Số các vectơ bằng vectơ \[\overrightarrow {OC} \] có điểm đầu và điểm cuối là các đỉnh của lục giác là:

A. 2

B. 3

C. 4

D. 6

Trong mặt phẳng Oxy cho điểm M(-5;9). Phép đối xứng tâm I(2; -6) biến M thành M’ thì tọa độ M’ là.

A. M’(9; ‒15).

B. M’(9; ‒3).

C. M’(9; ‒21).

D. M’(1; ‒3).

Trong mặt phẳng tọa độ (Oxy ) cho phép đối xứng tâm I(1; 2) biến điểm M (x; y) thành M'(x'; y'). Mệnh đề nào sau đây là đúng?

A. \(\left\{ {\begin{array}{*{20}{l}}{x' = - x + 2}\\{y' = - y - 2}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x' = - x + 2}\\{y' = - y + 4}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x' = - x + 2}\\{y' = - y - 4}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x' = x + 2}\\{y' = y - 2}\end{array}} \right.\).

Cho phương trình \({\rm{cot}}x = \sqrt 3 .\) Các nghiệm của phương trình là:

A. \(\frac{\pi }{3} + k\pi \)

B. \(\frac{\pi }{6} + k\pi \)

C. \(\frac{{5\pi }}{6} + k\pi \)

D. \( - \frac{\pi }{6} + k2\pi \)