91 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án (Phần 86)
Haylamdo biên soạn và sưu tầm 91 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
91 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án (Phần 86)
Câu 3:
Cho tam giác ABC cân tại A, đường cao AD, K là trung điểm của AD. Gọi I là hình chiếu của điểm D trên CK. Chứng minh rằng .
Câu 6:
Hình vẽ cho biết tam giác ABC vuông tại A, MN // BC, AB = 24cm, AM = 16cm, AN = 12cm. Tính độ dài x, y của các đoạn thẳng NC, BC.
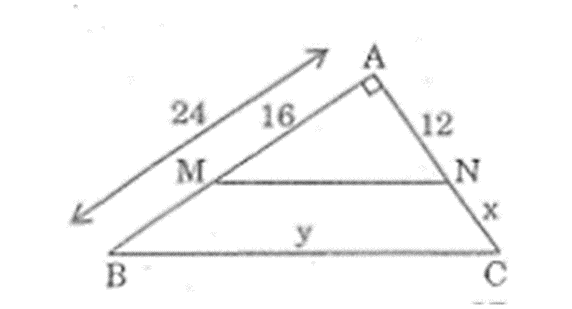
Câu 7:
Cho hình thoi ABCD có . Trên AB, AC lấy điểm M, N sao cho BM = CN. Chứng minh rằng MDN là tam giác đều.
Câu 8:
Cho hình bình hành ABCD có . Tia phân giác của qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:
a) AB = 2AD.
b) DI = 2AH.
c) AC vuông góc với AD.
Câu 11:
Cho 7 số tự nhiên khác nhau có tổng bằng 100. Chứng minh rằng trong 7 số luôn có 3 số mà tổng của chúng lớn hơn hoặc bằng 50.
Câu 13:
Với x > 0 cho biểu thức .
a) Rút gọn và tính giá trị P khi x = 4.
b) So sánh B với 1.
Câu 16:
Cho biểu thức .
a) Tìm ĐK để phân thức xác định.
b) Tìm giá trị của x để P = 1.
Câu 18:
Cho biểu thức: .
a) Rút gọn biểu thức Q với x > 0; x khác 4 và x khác 1.
b) Tìm giá trị của x để Q dương.
Câu 19:
Cho bốn số nguyên dương phân biệt sao cho tổng của mỗi hai số chia hết cho 2 và tổng của mỗi ba số chia hết cho 3. Tìm giá trị nhỏ nhất của tổng bốn số này?
Câu 20:
Cho x ∈ ℕ nhưng x ∉ ℕ* số x là:
A.1
B. Bất kì số tự nhiên nào
C. 0
D. Không tồn tại số x
Câu 22:
Cho hai góc kề bù và . Biết . Tính số đo góc để tia Ot là tia phân giác của góc .
Câu 24:
Câu 25:
Cho các số thực a, b, c thỏa mãn a + b + c = 0. Chứng minh rằng a5 + b5 + c5 chia hết cho 5.
Câu 26:
Cho các số thực a, b, c thỏa mãn a2 + b2 + c2 = 1.
Tìm GTLN của M = ab + bc + 2ac.
Câu 27:
Cho các số thực dương a, b, c thỏa mãn a + b + c = 3.
Chứng minh a2 + b2 + c2 + ab + bc + ca ≥ 6.
Câu 28:
Cho các số thực x, y thỏa mãn 4x2 + 2xy + y2 = 3.
Tìm GTLN, GTNN của P = x2 + 2xy – y2.
Câu 29:
Cho các số thực x, y thỏa mãn x + y = 1, x3 + y3 = 2.
Tính giá trị của biểu thức M = xy, N = x5 + y5.
Câu 30:
cho các tập hợp A = (2; +∞) và B =[m2 - 7; +∞) với m > 0. Tìm m để A\B là một khoảng có độ dài bằng 16.
Câu 32:
Cho đa thức P(x) với các hệ số nguyên thỏa mãn P(2021).P(2022) = 2023.
Chứng minh rằng đa thức P(x) - 2024 không có nghiệm nguyên.
Câu 35:
Cho cấp số cộng (un) và gọi Sn là tổng n số hạng đầu tiên của nó. Biết S7 = 77, S12 = 192. Tìm số hạng tổng quát un của cấp số cộng đó?
Câu 37:
Cho dãy số thập phân: 1,1; 2,2; 3,3; ......; 97,9; 99,0.
a) Số hạng thứ 50 của dãy là số nào?
b) Dãy số này có bao nhiêu số hạng?
c) Tính tổng của dãy số trên?
Câu 38:
Cho dãy số 1,1; 2,2; 3,3; …; 108,9; 110,0
a) Dãy số có bao nhiêu số hạng?
b) Số hạng thứ 30 của dãy là bao nhiêu?
Câu 40:
Câu 41:
Cho đường thẳng d song song với mặt phẳng (P). Mệnh đề nào sau đây đúng?
A. Đường thẳng d không có điểm chung với mặt phẳng (P).
B. Đường thẳng d có một điểm chung với mặt phẳng (P).
C. Đường thẳng d có đúng hai điểm chung với mặt phẳng (P).
D. Đường thẳng d có vô số điểm chung với mặt phẳng (P).
Câu 42:
Cho đường tròn (O) đường kính AB. Vẽ đường tròn (I) đường kính OA. Bán kính OC của đường tròn (I) cắt đường tròn (I) tại O. Vẽ CH ⊥ AB. Chứng minh tứ giác ACDH là hình thang cân.
Câu 43:
Cho đường tròn (O; R) có hai đường kính AB và CD vuông góc. Gọi I là điểm trên cung AC sao cho khi vẽ tiếp tuyến qua I và cắt DC kéo dài tại M thì IC = CM. Độ dài OM tính theo bán kính là?
Câu 44:
Cho ba điểm A, B, C trên đường tròn (O). Tiếp tuyến tại A cắt dây cung CB kéo dài tại điểm M. Chứng minh: .
Câu 45:
Cho đường tròn tâm O. Trên nửa đường tròn đường kính AB lấy hai điểm C, D. Từ C kẻ CH vuông góc với AB, nó cắt đường tròn tại điểm thứ hai là E. Từ A kẻ AK vuông góc với DC, nó cắt đường tròn tại điểm thứ hai là F. Chứng minh rằng:
a) Hai cung nhỏ CF và BD bằng nhau.
b) Hai cung nhỏ BF và DE bằng nhau.
c) DE = BF.
Câu 46:
Cho . Khẳng định nào sau đây đúng?
A. sin(α – π) ≥ 0
B. sin(α – π) ≤ 0
B. sin(α – π) ≤ 0
Câu 47:
Cho = 70°, = 55°, tia Ax là tia phân giác của .
a) Tính số đo của
b) Chứng minh: Ax // BC.
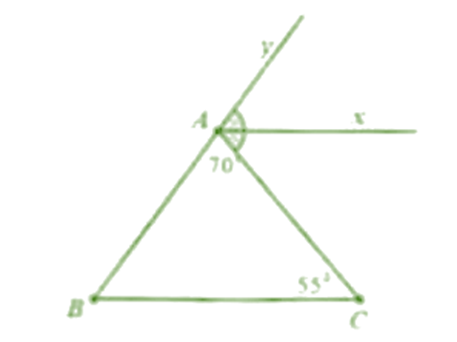
Câu 48:
Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm A, B sao cho A nằm giữa O và B. Trên cạnh Oy lấy hai điểm C, D sao cho C nằm giữa O và D.
Chứng minh rằng: AB + CD < AD + BC.
Câu 49:
Cho góc . Vẽ tia Oz là tia đối của tia Ox. Vẽ tia Om là tia phân giác của góc .
a) Tính góc ?
b) Vẽ tia On là tia đối của tia Om. Tia Ox có là tia phân giác của góc không? Vì sao?
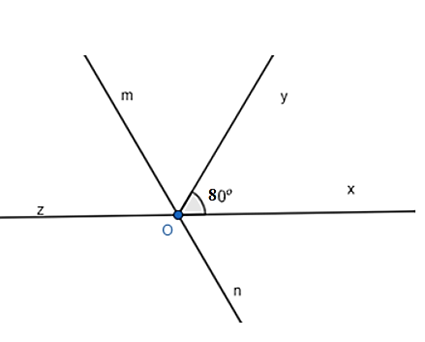
Câu 50:
cho hai đường thẳng a và b cắt đường thẳng c. Để có một cặp góc so le trong bằng nhau thì điều gì sau đây không thể xảy ra?
A. Các cặp góc đồng vị bằng nhau.
B. Các cặp góc so le ngoài bằng nhau.
C. Các cặp góc trong cùng phía bằng nhau.
D. Các cặp góc trong cùng phía bù nhau.
Câu 51:
Câu 52:
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC.
a) Chứng minh rằng tứ giác DBCE là hình thoi.
b) Gọi I là giao điểm của EC và đường tròn (O'). Chứng minh rằng ba điểm D, A, I thẳng hàng.
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O').
Câu 53:
Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’ và N’. Chứng minh
a) (ADF) // (BCE).
b) M′N′ // DF.
c) (DEF) // (MM′N′N) và MN // (DEF).
Câu 54:
Cho hai số thực a , b thỏa điều kiện ab = 1, a + b ≠ 0. Tính giá trị của biểu thức:
Câu 55:
Cho hai tập hợp E = (2;5] và F = [2m - 3; 2m + 2]. Tìm tất cả các giá trị của tham số m để E hợp F là một đoạn có độ dài bằng 5.
Câu 56:
Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.
Câu 57:
Cho hàm số y = x – 2 có đồ thị là đường thẳng (d).
a, Vẽ đồ thị hàm số đã cho.
b, Gọi A, B lần lượt là giao điểm của (d) với Ox, Oy. Tính diện tích tam giác OAB (đơn vị đo trên các trục tọa độ centimet).
c, Tìm giá trị của m để đường thẳng (d) và đường thẳng (d1): y = -2x + m² - 3 cắt nhau tại một điểm trên trục tung.
Câu 58:
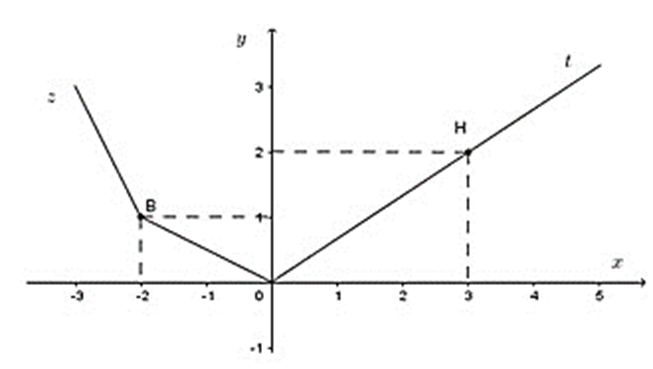
Cho hàm số f(x) hàm số y = f'(x) liên tục trên ℝ và có đồ thị như hình vẽ bên. Với giá trị nào của tham số m thì phương trình f(x) = 3x + m có nghiệm thuộc khoảng (-1;1).
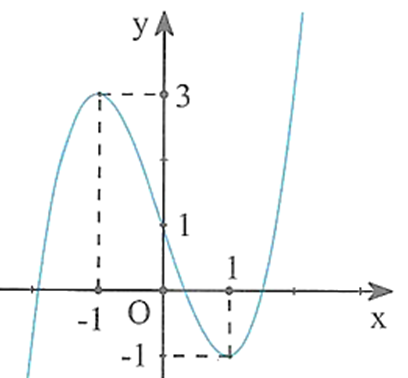
A. f(−1) + 3 < m < f(1) – 3.
B. f(−1) + 3 < m < f(1) + 3.
C. f(1) + 3 < m < f(-1) − 3.
D. f(0) – 1 < m < f(0) + 1.
Câu 60:
Xác định hàm số y = ax + b, biết đồ thị của hàm số đi qua hai điểm A(−2; 5) và B(1; −4).
Câu 62:
A. (-∞;-1).
B. (-1;3).
C. (1;+∞).
D. (3;+∞).
Câu 63:
Cho hàm số y = (m + 1)x + 3 (d) (m là tham số, m ≠ −1). Đường thẳng d cắt đường thẳng tại điểm M. Gọi N và P lần lượt là giao điểm của đường thẳng (d) và (d′) với trục hoành Ox. Tìm m để diện tích tam giác OMP bằng 2 lần diện tích tam giác OMN.
Câu 64:
Câu 65:
Cho hàm số f(x) = 4x2 − 4mx + m2 − 2m + 2 (m là tham số). Gọi S là tập hợp tất cả các giá trị của m sao cho . Khẳng định nào đúng?
A. S ⊂ (-4; 6).
B. S ⊂ (-3; 7).
C. S ⊂ [-2; 8].
D. S ⊂ [-1; 9].
Câu 66:
Cho hàm số bậc nhất y = (m – 2)x + 3. Tìm các giá trị của m để hàm số đồng biến.
Câu 67:
Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số có đúng 3 điểm cực trị.
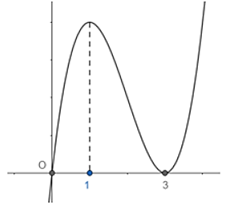
Câu 69:
Cho hàm số: y = mx + 1 (1), trong đó m là tham số. Tìm m để đồ thị hàm số (1) đi qua điểm A(1; 4). Với giá trị m vừa tìm được, hàm số (1) đồng biến hay nghịch biến trên R?
Câu 70:
Câu 71:
A. Hàm số đồng biến trên mỗi khoảng (-∞; -1) và (-1; +∞).
B. Hàm số nghịch biến với mọi x khác 1.
C. Hàm số nghịch biển trên tập ℝ\{-1}.
D. Hàm số nghịch biến trên mỗi khoảng (-∞; -1) và (-1; +∞).
Câu 72:
Cho phương trình x2 – 5mx – 4m = 0 với m là tham số. Chứng minh rằng khi phương trình có 2 nghiệm phân biệt x1, x2 thì x12 + 5mx2 + m2 + 14m + 1 > 0.
Câu 73:
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = -x3 + 3x2 – 4. Nêu nhận xét về đồ thị của hàm số này.
Câu 74:
Cho hàm số y = x2 – x – 2. Khảo sát sự biến thiên và vẽ đồ thị hàm số (P) của hàm số.
Câu 75:
Cho hình bình hành ABCD với AD = 2AB. Từ C vẽ CE vuông góc với AB. Nối E với trung điểm M của AD. Từ M vẽ MF vuông góc với CE, MF cắt BC tại N.
a) Tứ giác MNCD là hình gì?
b) Tam giác EMC là tam giác gì?
c) Chứng minh: .
Câu 79:
Cho hình vẽ biết AB // CD < AD // BC, AC cắt BD tại O. Chứng minh
a) AB = CD; AD = BC.
b) OA = OC; OB = OD.
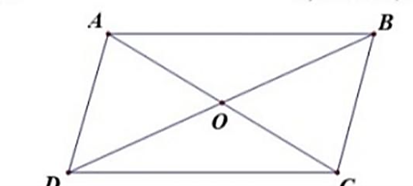
Câu 80:
Cho ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Gọi K là giao điểm của AC và DM, L là trung điểm cuả BD và CM.
a. MNPQ là hình gì?
b. MDPB là hình gì?
Câu 81:
Cho hình bình hành ABCD có , AB = 10cm, AD = 15cm. Tia phân giác của cắt BC tại E.
a) Chứng minh: tam giác ABE cân.
b) Tính EC.
c) Tính SABCD.
Câu 82:
Cho hình bình hành ABCD biết BD vuông góc với BC, AB = a, . Tính S hình bình hành theo a và α?
Câu 83:
Cho hình bình hành ABCD có ; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.
a) MCND là hình thoi.
b) ABMD là hình thang cân.
Câu 84:
Cho hình bình hành ABCD. Gọi K, I lần lượt là trung điểm của AB và CD. Gọi M, N là giao điểm của AI, CK với BD. Chứng minh: ∆ADM = ∆CBN.
Câu 85:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, ; SO ⊥ (ABCD) và . Tính thể tích khối chóp S.ABCD.
Câu 86:
Cho hình chóp S.ABCD . Gọi M, N lần lượt là trung điểm của SB và SD. Thiết diện của hình chóp S.ABCD và mặt phẳng (AMN) là hình gì?
A. Tam giác.
B. Ngũ giác.
C. Tam giác cân.
D. Tứ giác.
Câu 87:
Cho chóp S.ABCD. M, N lần lượt là trung điểm của SB, SD. Tìm giao điểm của (AMN) và SC.
Câu 88:
Cho hình chóp S.ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD.
Tìm giao tuyến của hai mặt phẳng
a) (SBM) và (SCD);
b) (ABM) và (SCD);
c) (ABM) và (SAC).
Câu 89:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn BC = 2a đáy bé AD = a , AB = b. Mặt bên SAD là tam giác đều. M là một điểm di động trên AB, Mặt phẳng (P) đi qua M và song song với SA, BC.1. Tìm thiết diện của hình chóp khi cắt bởi mp (P). Thiết diện là hình gì?
Câu 90:
Cho hình chóp S.ABCD. M là một điểm trên cạnh SC.
a) Tìm giao điểm của AM và (SBD).
b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN).
Câu 91:
Cho hình chóp S.ABCD, AB và CD không song song và M là trung điểm của SC.
a, Tìm N = SD ∩ (MAB).
b, Gọi O = AC ∩ BD. Chứng minh SO, AM, BN đồng quy.