92 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 62)
Haylamdo biên soạn và sưu tầm 92 bài tập trắc nghiệm tổng hợp môn Toán có lời giải chi tiết giúp học sinh lớp 12 biết cách làm bài tập & ôn luyện trắc nghiệm môn Toán.
92 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án ( Phần 62)
Câu 8:
Trong mặt phẳng tọa độ Oxy có hai vectơ đơn vị trên hai trục là . Cho , nếu thì (a; b) có thể là cặp số nào sau đây?
A. (2; 3);
B. (3; 2);
C. (−3; 2);
Câu 9:
Xét các số phức z thỏa mãn là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng:
Câu 10:
Xét các số phức z thỏa mãn là số thuần ảo. Biết rằng tập hợp tất cả các điểm biểu diễn của z là một đường tròn, tâm của đường tròn đó có tọa độ là:
Câu 11:
A. m = 4;
B. m = 0, m = 1;
C. m = 1;
Câu 13:
Cho hình lập phương (ABCD.A'B'C'D') (tham khảo hình vẽ bên). Góc giữa hai đường thẳng (AC) và (A'D) bằng:
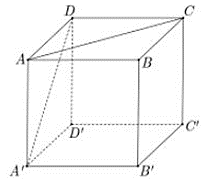
Câu 14:
Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa các cặp đường thẳng sau đây:
a) AB và B'C'
b) AC và B'C'
c) A'C' và B'C
Câu 17:
Gọi A, B lần lượt là điểm cực đại và điểm cực tiểu của đồ thị hàm số y = x3 − 3x2 + 2. Trung điểm I của đoạn thẳng AB có tọa độ nào dưới đây?
A. (1; 1);
B. (2; 0);
C. (1; 0);
Câu 18:
Gọi A, B lần lượt là điểm cực đại và cực tiểu của đồ thị hàm số y = x3 − 3x. Tính độ dài đoạn thẳng AB?
Câu 19:
Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc 45°. Tính thể tích của khối chóp S.ABC theo a.
Câu 20:
Hình chóp tam giác đều S.ABC có cạnh đáy là a và cạnh bên tạo với đáy một góc 45°. Tính theo a thể tích khối chóp S.ABC.
Câu 23:
Cho ba điểm A(−1; 1), B(1; 3), C(−2; 0)
a) Chứng minh A, B, C thẳng hàng
b) Tìm các tỉ số mà A chia đoạn BC, B chia đoạn AC và C chia đoạn AB
Câu 24:
Câu 25:
Xét các số phức z thỏa mãn . Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn của các số phức là một đường tròn bán kính bằng bao nhiêu?
Câu 26:
Cho khối tròn xoay có thể tích bằng pa3, chiều cao h = 2a. Tìm bán kính đáy r của khối trụ đó.
Câu 27:
Cho khối trụ tròn xoay có diện tích toàn phần gấp 2 lần diện tích xung quanh và có bán kính đáy bằng 6 cm. Tính thể tích khối trụ đó.
Câu 28:
Cho khối lăng trụ ABC.A'B'C' có thể tích bằng a. Gọi M là trung điểm của AB. Nếu tam giác MB'C' có diện tích bằng b thì khoảng cách từ C đến mặt phẳng (MB'C') bằng bao nhiêu?
Câu 29:
Câu 30:
Cho hình thang ABCD có AB song song với CD. Cho AB = 2a và CD = a. Gọi O là trung điểm của AD. Khi đó:
A.
B.
C.
D.
Câu 31:
Trong không gian, cho hình thang cân ABCD có AB // CD, AB = a, CD = 2a, AD = a. Gọi M, N lần lượt là trung điểm của AB. CD. Gọi K là khối tròn xoay được tạo ra khi quay hình thành ABCD quanh trục MN. Tính diện tích toàn phần Sep của khối K.
Câu 32:
Cho tam giác ABC vuông cân tại A, BC = a. Quay hình tròn ngoại tiếp tam giác vuông ABC xung qunah cạnh BC ta được một khối tròn xoay có thể tích bằng:
Câu 33:
Cho tam giác ABC cân tại A, góc và AB = 4 cm. Tính thể tích khối tròn xoay lớn nhất có thể khi ta quay tam giác ABC xung quanh đường thẳng chứa một cạnh của tam giác ABC.
Câu 34:
Cho hình chóp S.ABCD. Gọi M là trung điểm SB, N thuộc SC sao cho SN = 2NC. Tìm giao điểm của SA và mp (DMN).
Câu 35:
Cho hình chóp S.ABCD, gọi M là trung điểm SB và N là điểm thuộc cạnh SC sao cho SN = 2NC. Tính tỉ số .
Câu 36:
Cho hai hàm số f (x) = ax3 + bx2 + cx − 2 và g (x) = dx2 + ex + 2 (a, b, c, d, e Î ℝ). Biết rằng đồ thị của hàm số y = f (x) và y = g (x) cắt nhau tại ba điểm có hoành độ lần lượt là −2; −1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
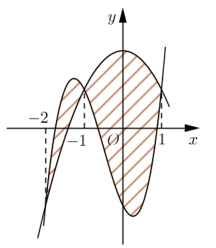
Câu 37:
Cho hai hàm số và g (x) = dx2 + ex + 1 (a, b, c, d, e Î ℝ). Biết rằng đồ thị hàm số y = f (x) và y = g (x) cắt nhau tại ba điểm có hoành độ lần lượt là −3; −1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
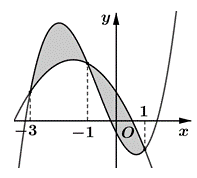
Câu 38:
Cho tam giác ABC. Hãy xác định các điểm I, J, K, L thoả các đẳng thức sau:
a)
b)
c)
d)
Câu 39:
Cho ∆ABC. Hãy xác định các điểm I, J, K, L thoả các đẳng thức sau:
a)
b)
c)
d)
Câu 40:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD (tham khảo hình vẽ bên). Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CMN.
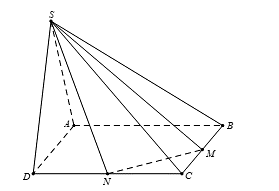
Câu 41:
Câu 42:
Cho hình nón có bán kính đáy bằng 5. Biết rằng khi cắt hình nón cho bởi mặt phẳng qua trục, thiết diện thu được là một tam giác đều. Diện tích toàn phần của hình nón đã cho bằng:
Câu 43:
Cho hình nón có bán kính bằng 5 và góc ở đỉnh bằng 60°. Diện tích xung quanh của hình nón đã cho bằng:
Câu 44:
Câu 45:
Cho hình nón đỉnh S có đáy là hình tròn tâm O. Một mặt phẳng qua đỉnh của hình nón và cắt hình nón theo thiết diện là tam giác vuông có diện tích bằng 4. Góc giữa đường cao của hình nón và mặt phẳng thiết diện bằng 30°. Tính thể tích của khối nón được giới hạn bởi hình nón đã cho.
Câu 46:
A.
B.
C. Cả A, B đều đúng;
Câu 47:
Cho hình thang ABCD có hai đáy AB và CD với AB = 2CD. Từ C vẽ .
a) Chứng minh I là trung điểm AB và ;
b) Chứng minh .
Câu 48:
Cho tứ giác ABCD. Các điểm M, N theo thứ tự thay đổi trên các cạnh AD, BC sao cho . Lấy I là trung điểm cạnh MN. Các điểm E, F lần lượt là trung điểm của AC và BD. Chứng minh I luôn chuyển động trên đoạn EF.
Câu 49:
Cho tứ diện ABCD. Trên cạnh AD, BC theo thứ tự lấy các điểm M, N sao cho . Gọi (P) là mặt phẳng chứa đường thẳng MN và song song với CD. Khi đó thiết diện của tứ diện ABCD cắt bởi mặt phẳng (P) là
A. Một hình bình hành;
B. Một hình thang với đáy lớn gấp 2 lần đáy nhỏ;
C. Một hình thang với đáy lớn gấp 3 lần đáy nhỏ;
Câu 50:
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AD, BC
a) Chứng minh:
b) Xác định điểm O sao cho .
Câu 51:
Câu 52:
Cho hình chóp tam giác đều S.ABC có đáy bằng 3a, góc giữa cạnh bên và mặt đáy bằng 45°. Thể tích khối cầu ngoại tiếp hình chóp S.ABC bằng:
Câu 53:
Câu 54:
Lãi suất gửi tiết kiệm của ngân hàng A thời gian vừa qua thay đổi liên tục. Bạn Duy gửi số tiền ban đầu là 10 triệu đồng với lãi suất 0,8% một tháng. Chưa đầy một năm, thì lãi suất tăng lên 1,2% một tháng trong nửa năm tiếp theo. Và bạn Duy tiếp tục gửi; sau nửa năm đó lãi suất giảm xuống còn 1% một tháng. Đồng thời bạn Duy quyết định gửi thêm một số tháng tròn nữa. Biết rằng khi rút tiền bạn Duy được cả vốn lẫn lãi là 12 153 337,95 triệu đồng. Tổng số tháng mà bạn Duy gửi tiết kiệm là:
Câu 55:
Lãi suất gửi tiền tiết kiệm của các ngân hàng trong thời qua liên tục thay đổi. Bác Mạnh gửi vào một số ngân hàng số tiền 5 triệu đồng với lãi suất 0,7%/ tháng. Sau sáu tháng gửi tiền, lãi suất tăng lên 0,9%/ tháng. Đến tháng thứ 10 sau khi gửi tiền, lãi suất giảm xuống 0,6%/ tháng và giữ ổn định. Biết rằng nếu bác Mạnh không rút tiền ra khỏi ngân hàng thì cứ sau mỗi tháng, số tiền lãi sẽ được nhập vào vốn ban đầu (ta gọi đó là lãi kép). Sau một năm gửi tiền, bác Mạnh rút được số tiền là bao nhiêu? (biết trong khoảng thời gian này bác Mạnh không rút tiền ra).
Câu 56:
Với các chữ số 2, 3, 4, 5, 6, có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số khác nhau trong đó hai chữ số 2, 3 không đứng cạnh nhau?
Câu 57:
Từ các chữ số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho hai chữ số 1 và 2 luôn đứng cạnh nhau?
Câu 60:
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V?
Câu 61:
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I Î AC, J Î DN sao cho IJ // BM. Độ dài IJ theo a là:
Câu 62:
Câu 63:
Câu 64:
Một chiếc bút chì có dạng khối lăng trụ lục giác đều có cạnh đáy 3 mm và chiều cao bằng 200 mm. Thân bút chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng khối trụ có chiều cao bằng chiều dài của bút và đáy là hình tròn có bán kính 1 mm. Giả định 1 m3 gỗ có giá a (triệu đồng), 1 m3 than chì có giá 6a (triệu đồng). Khi đó giá nguyên vật liệu làm một chiếc bút chì như trên gần nhất với kết quả nào dưới đây?
A. 84,5.a (đồng);
B. 78,2.a (đồng);
C. 8,45.a (đồng);
Câu 65:
Một chiếc bút chì có dạng khối lăng trụ lục giác đều có cạnh đáy 3 mm và chiều cao bằng 200 mm. Thân bút chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng khối trụ có chiều cao bằng chiều dài của bút và đáy là hình tròn có bán kính 1 mm. Giả định 1 m3 gỗ có giá a (triệu đồng), 1 m3 than chì có giá 8a (triệu đồng). Khi đó giá nguyên vật liệu làm một chiếc bút chì như trên gần nhất với kết quả nào dưới đây?
A. 9,7.a (đồng);
B. 97,3.a (đồng);
C. 90,7.a (đồng);
Câu 66:
Một hộp chưa 35 quả cầu gồm 20 quả màu đỏ được đánh số từ 1 đến 20 và 15 quả màu xanh được đánh số từ 1 đến 15. Lấy ngẫu nhiên từ hộp đó một quả cầu. Tính xác suất để lấy được quả màu đỏ hoặc ghi số lẻ.
Câu 67:
Một bình đựng 35 quả cầu phân biệt, trong đó có 20 quả cầu màu xanh và 15 quả cầu màu đỏ. Chọn ngẫu nhiên 5 quả cầu. Xác suất để trong 5 quả cầu được chọn có cả quả cầu màu xanh và quả cầu màu đỏ là:
Câu 68:
Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Tính số cách xếp sao cho các nữ sinh luôn ngồi cạnh nhau.
Câu 69:
Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho các nữ sinh luôn ngồi cạnh nhau và các nam sinh luôn ngồi cạnh nhau?
Câu 70:
Trong mặt phẳng Oxy, cho tam giác ABC có đường cao AH, trung tuyến CM và phân giác trong BD có phương trình x + y − 5 = 0, biết H(−4; 1), . Tọa độ đỉnh A là:
Câu 71:
Câu 72:
Trong mặt phẳng Oxy, cho các điểm A(1; −2), B(4; 1), C(4; −5).
a) Chứng minh A, B, C là ba đỉnh của một tam giác. Tìm tọa độ trung điểm cạnh BC và tọa độ trọng tâm G của tam giác ABC.
b) Điểm I thỏa mãn . Tìm tọa độ điểm I.
c) Xét hình thang ABCD với hai đáy AB và CD thỏa mãn AB = 2CD. Tìm tọa độ đỉnh D.
Câu 77:
Tìm giá trị thực của tham số m để đường thẳng d: y = (2m − 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 1.
Câu 78:
Tìm giá trị thực của tham số m để đường thẳng d: y = (3m + 1)x + 3 + m vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 − 1.
Câu 80:
Cho hàm số f (x) có đạo hàm f ¢(x) = x(x + 2)2, "x Î ℝ. Số điểm cực trị của hàm số đã cho là:
Câu 81:
Cho hàm số f (x) có đạo hàm f ¢(x) = x(x − 2)2, "x Î ℝ. Số điểm cực trị của hàm số đã cho là:
Câu 83:
Cho ba điểm O, A, B thẳng hàng và biết OA = a, OB = b. Tính tích vô hướng trong hai trường hợp:
a) Điểm O nằm ngoài đoạn AB;
b) Điểm O nằm trong đoạn AB.
Câu 88:
Cho hình chóp tứ giác đều S.ABCD có , côsin của góc hợp bởi hai mặt phẳng (SBC); và (SCD) bằng . Tính thể tích của khối chóp S.ABCD.
Câu 89:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có hai tiệm cận đứng:
Câu 90:
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số có hai tiệm cận ngang.
Câu 91:
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC) và đáy ABC là tam giác vuông tại B, AB = a, SA = a. Gọi H là hình chiếu của A trên SB. Tính khoảng cách giữa AH và BC.
Câu 92: