90 bài tập trắc nghiệm tổng hợp môn Toán 2024 cực hay có đáp án (Phần 89)

Cho x + y = 15. Tìm min, max $B=\sqrt{x-4}+\sqrt{y-3}$

Cho x,y,z là các số nguyên thỏa mãn: (x - y)(y - z)(z – x) = x + y + z. Chứng minh x + y + z chia hết cho 27.

Cho x, y, z thỏa mãn đk x + y + z = a. Tìm GTNN của $P=\left(1+\frac{a}{x}\right)\left(1+\frac{a}{y}\right)\left(1+\frac{a}{z}\right)$

Cho x + 3y – 4 = 0, tính x³ - x² + 9x²y - 9y² + 27xy² + 27y³ - 6xy

Chứng tỏ rằng (2²⁰²² + 2²⁰²¹ + 2²⁰²⁰) chia hết cho 7.

Tìm các hệ số a, b, c biết: (ax + b)(x² – cx + 2) = x³ + x² – 2 với mọi x

Chứng minh $\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+\frac{1}{4\sqrt{3}}+\mathrm{...}+\frac{1}{2005\sqrt{2004}}<2$

Chứng minh $\frac{1}{65}<\frac{1}{5^3}+\frac{1}{6^3}+\mathrm{...}+\frac{1}{{2004}^3}<\frac{1}{40}$

Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. Kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng: Tổng $\frac{1}{D{I}^2}+\frac{1}{D{K}^2}$ không đổi khi I thay đổi trên cạnh AB.

Chứng minh rằng F = 10²⁸ + 8 chia hết cho 72

Chứng minh $\frac{1-2{\sin }^{2}x}{1+\sin 2x}=\frac{1-\tan x}{1+\tan x}$

Chứng minh tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Cho $\frac{a}{b}=\frac{c}{d}$ với a, b, c, d khác 0. Chứng minh $\frac{a}{a-b}=\frac{c}{c-d}$

Cho tứ giác ABCD. Chứng minh $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$

Cho tam giác ABC có BC = a, AC = b, Ab = c, đường phân giác AD.

1. Tính độ dài BD, DC.

2. Tia phân giác của góc B cắt AD tại I. Tính tỉ số AI : ID.

3. Cho BC bằng trung bình cộng của AB và AC, gọi G là trọng tâm của tam giác ABC. Chứng minh IG song song BC.

Chứng minh biểu thức $A=-x^2+\frac{2}{3}x-1$ luôn âm với mọi giá trị của biến

Chứng minh biểu thức sau luôn âm với mọi x: –x² – 6x – 15

Chứng minh với a, b dương thì $\sqrt{a+b}<\sqrt{a}+\sqrt{b}$

Có tồn tại hay không một dãy gồm 2019 số tự nhiên liên tiếp mà các số đó đều là hợp số?

Chứng minh đẳng thức sau: $\frac{\left(\sin x+\cos x\right)}{{\sin }^{3}x}={\cot }^{3}x+{\cot }^{2}x\cot x+1$

Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O). Tiếp tuyến tại A của (O) cắt đường thẳng BC tại D. Gọi E là trung điểm của AD. Chứng minh EC là tiếp tuyến của (O).

Chứng minh tam giác ABC có h_a = 2R.sinB.sinC

Chứng minh n⁵ – n chia hết cho 30 với mọi số nguyên n.

Cho (O) và A là điểm nằm ngoài (O). Qua A vẽ tiếp tuyến AB, AC với (O) với B,C là tiếp điểm. OA cắt BC tại DA

a) Chứng minh OA là đường trung trực BC.

b) Chứng minh OD.DA = BD²

c) Vẽ đường kính BE, AE cắt (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh OD.OA = OG.OH

d) Chứng minh EH là tiếp tuyến của (O)

Chứng tỏ rằng số có dạng $\overline{aaa}$ bao giờ cũng chia hết cho 37.

Chứng minh rằng: Nếu p là một số nguyên tố lớn hơn 3 và 2p + 7 cũng là số nguyên tố thì 4p + 7 là một hợp số.

Cho tam giác ABC nhọn, đường cao AH. Gọi M, N lần lượt là hình chiếu cùa H lên AB và AC.

a) Chứng minh: AM.AB = AN.AC.

 b) Chứng minh: $\frac{S_{AMN}}{S_{ACB}}={\sin }^{2}B.{\sin }^{2}C$

Cho tam giác ABC vuông tại A, đường cao AH. Trên AC lấy điểm K ( K khác A và C), gọi D là hình chiếu của A trên BK. Cho biết BC = 4BH.

Chứng minh rằng: $S_{BHD}=\frac{1}{4}{S}_{BKC}.{\cos }^2\widehat{ABD}$

Chứng minh $\frac{1-\cos 2x}{\sin 2x}=\tan x$

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC. Chứng minh:

a) ∆ABH = ∆ACH

b) AH là tia phân giác của góc BAC.

Chứng minh rằng trong 1 tam giác vuông, trung tuyến ứng với cạnh huyền nửa cạnh huyền

Chứng minh rằng với mọi n ∈ ℕ thì n(2n + 7)(7n + 1) chia hết cho 6

Chứng tỏ rằng A = 1 + 4 + 4² + … + 4²⁰²¹ chia hết cho 21.

Chứng minh rằng A = 3^{5n + 2} + 3^{5n + 1} – 3⁵ⁿ chia hết cho 11 với mọi n ∈ ℕ

Chứng minh rằng số dư trong phép chia một số nguyên tố cho 30 chỉ có thể là 1 hoặc là số nguyên tố. Khi chia cho 60 thì kết quả ra sao

Chứng minh rằng với mọi số tự nhiên n thì (n + 2022)(n + 2023) chia hết cho 2

Cho 3 số tự nhiên a b c không chia hết cho 4. Khi chia a b c cho 4 thì có số dư khác nhau. Chứng minh a + b + c chia hết cho 2

Có 35 viên bi trong đó có 7 viên màu xanh 8 viên màu đỏ và 20 viên bi màu vàng vậy số bi màu xanh chiếm bao nhiêu phần của tổng số bi ?

Có 5 công nhân làm trong 6 giờ được 120 sản phẩm. Hỏi 4 công nhân làm trong bao nhiêu giờ thì được 96 sản phẩm? (mức làm mỗi người như nhau)

Có 6 học sinh sẽ được sắp xếp ngồi vào 6 chỗ đã được ghi số thứ tự trên 1 bàn dài.

1.Tìm số cách sắp xếp 6 học sinh này ngồi vào bàn.

2. Tìm số cách sắp xếp 6 học sinh này ngồi vào bàn sao cho 2 học sinh A và B không ngồi cạnh nhau.

Cho tam giác ABC, D và I là các điểm được xác định bởi

$3\overrightarrow{DB}-2\overrightarrow{DC}=\overrightarrow{0};\overrightarrow{IA}+3\overrightarrow{IB}-2\overrightarrow{IC}=\overrightarrow{0}$.

a) Biểu diễn AD theo $\overrightarrow{AB},\overrightarrow{AC}$

b) Chứng minh A, I, D thẳng hàng

Cho tam giác ABC có AB = 6cm, AC = 8cm, BC = 10cm.

a) Chứng minh tam giác ABC vuông.

b) Tính góc B và góc C.

Cho tam giác ABC có AB = 4, AC = 6 và trung tuyến BM = 3. Tính cạnh BC?

Cho tam giác ABC có $\widehat{B}+\widehat{C}=60°$; AB = 3; AC = 6. Tính độ dài đường phân giác AD?

Tam giác ABC có $BC=\sqrt{5};AC=3;\cot C=-2$. Tính cạnh AB?

Tam giác ABC có BC = 12, CA = 9, AB = 6. Điểm M nằm trên cạnh BC sao cho BM = 4. Độ dài AM bằng bao nhiêu?

Cho tam giác ABC có BC = a, AC = b, AB = c. Đường trung tuyến AM = AB = c. Chứng minh rằng a² = 2(b² – c²)

Cho tam giác ABC nhọn AB < AC. Các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC. Kẻ Bx, Cy lần lượt vuông góc với AB, AC chúng cắt nhau tại K.

1. Chứng minh tứ giác BHCK là hình bình hành và H, M, K thẳng hàng

2. Gọi I là điểm đối xứng với H qua BC. Chứng minh tứ giác BIKC là hình thang cân

3. Gọi G là giao điểm của BK và HI, tam giác ABC phải có thêm điều kiện gì để tứ giác GHCK là hình thang cân.

Tam giác ABC vuông tại A và có AB = AC = a. Tính độ dài đường trung tuyến BM của tam giác đã cho.

Cho tam giác ABC vuông tại A có AB = 6cm , BC = 10cm. Tính sinC, tan C, cos C, cotC, sinB, cosB, tanB, cotB

Cho ΔABC có hai trung tuyến CM, BN bằng nhau và cắt nhau tại G. Chứng minh tam giác ABC cân.

Cho tam giác có ba cạnh lần lượt là 5,6,7. Tìm độ dài đường cao ứng với cạnh có độ dài bằng 6.

Tìm tất cả các giá trị thực của m để đồ thị hàm số y = x³ − 3mx² + 4m³ có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa độ.

Trên đoạn thẳng AB lấy một điểm M (MA > MB). Trên cùng một nửa mặt phẳng có bờ AB, vẽ các tam giác đều AMC, BMD. Gọi E, F, I, K theo thứ tự là trung điểm của CM, CB, DM, DA. Chứng minh rằng EFIK là hình thang cân và $KF=\frac{1}{2}CD$

Trong tam giác ABC, nếu có 2h_a​ = h_b ​+ h_c​ thì:

Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M là trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H

a) Tứ giác AMBQ là hình gì?

b) Chứng minh CH vuông góc AB

c) Chứng minh tam giác PIQ cân

Cho tam giác ABC vuông tại A (AB < AC) đường cao AH

1) Giả sử AB = 9cm, AC = 12cm. Tỉnh độ dài các đoạn thẳng BC, BH và AH.

2) Gọi M và N lần lượt là chân các đường vuông góc kẻ từ điểm H đến các đường

thằng AB và AC . Chứng minh AM.AB = AN.AC.

3) Đường thẳng đi qua điểm A và song song với đường MN cắt đường thẳng đi qua điểm C và song song với đường AH tại điểm K. Gọi I là giao điểm của AH và BK. Chứng minh ba điểm M, L, N là ba điểm thẳng hàng.

Trong hình tam giác đều, khẳng định nào sau đây là đúng?

A. Ba cạnh bằng nhau và bằng 3 cm.

B. Ba góc bằng nhau và bằng 90°.

C. Ba cạnh bằng nhau, ba góc không bằng nhau.

D. Ba cạnh bằng nhau, ba góc bằng nhau và bằng 60°.

Khi quay 1 hình tam giác vuông một vòng quanh một cạnh góc vuông cố định ta được hình gì?

Cho tam giác ABC vuông tại A (AB <AC), M là trung điểm của BC. Kẻ ME vuông góc AB (E thuộc AB), kẻ MF vuông góc AC (F thuộc AC ).

a) Tứ giác AEMF là hình gì? Vì sao?

b) Chứng minh EF = $\frac{1}{2}$BC

c) Gọi K là chân đường vuông góc kẻ từ A đến BC. Chứng minh rằng tứ giác EKMF là hình thang cân.

Nhà bạn Thu có một đèn trang trí có dạng hình chóp tam giác đều như Hình 10.16. Các cạnh của hình chóp đều bằng nhau và bằng 20 cm. Bạn Thu dự định sẽ dán các mặt bên của đèn bằng những tấm giấy màu. Tính diện tích giấy bạn Thu sử dụng (coi như mép dán không đáng kể). Cho biết $\sqrt{300}\approx \mathrm{17,32}$

Cho tam giác ABC có góc B bằng 120° , BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D.

a) Tính độ dài đường phân giác BD

b) Gọi M là trung điểm của BC. Chứng minh AM ⊥ BD

Cho (O ; 4cm) có 2 đường kính AB và CD vuông góc tại O. Lấy I trên OC sao cho OI = 3cm. AI cắt (O) tại M. Tính AM và đường cao MH của ΔAMB

Nêu tính chất đường trung tuyến trong tam giác vuông.

Cho hình chóp tứ giác S.ABCD, M là một điểm trên cạnh SB. Gọi E, F là hai điểm lần lượt thuộc miền trong tam giác ABD và tam giác BCD. Tìm giao tuyến của mặt phẳng (MEF) và mặt phẳng (SCD).

Chu vi của một tam giác là 81cm. Các cạnh của nó tỉ lệ với 2, 3, 4. Tính độ dài mỗi cạnh.

Chứng minh rằng $\frac{1}{n\left(n+1\right)}=\frac{1}{n}-\frac{1}{n+1}\left(n\in {\mathbb{N}}^{*}\right)$

Giả sử AB là một dây cung của đường tròn (O). Trên cung nhỏ AB lấy các điểm C và D sao cho $\stackrel{⏜}{AC}=\stackrel{⏜}{BD}$. Chứng minh AB và CD song song.

Cho 10a² – 3b² + ab = 0 với b > a > 0. Tính $M=\frac{2a-b}{3a-b}+\frac{5b-a}{3a+b}$.

Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F.

a) Chứng minh E và F đối xứng với nhau qua AB.

b) Chứng minh tứ giác MEBF là hình thoi.

c) Hình bình hành ABCD có thêm điều kiện gì để tứ giác BCNE là hình thang cân.

Cho $\overline{abc}-\overline{\mathrm{deg}}$ chia hết cho 7. Chứng minh $abcdeg$ chia hết cho 7.

Cho hình bình hành ABCD có $\widehat{A}=120°$. Tia phân giác của $\widehat{D}$ qua trung điểm I của AB. Kẻ AH vuông góc với DC. Chứng minh rằng:

a) AB = 2AD.

b) DI = 2AH.

c) AC vuông góc với AD.

Cho 3 số nguyên tố lớn hơn 3 trong đó số sau lớn hơn số trước d đơn vị. Chứng minh rằng d chia hết cho 6.

Cho Parabol (P): y = x² và đường thẳng (d) : y = 2(m + 3)x – 2m + 2 (m là tham số, m thuộc R).

a) Với m = - 5 tìm tọa độ giao điểm của parabol (P) và đường thẳng (d).

b) Chứng minh rằng: Parabol (P) và đường thẳng (d) cắt nhau tại hai điểm phân biệt với mọi m. Tìm m để (d) cắt (P) tại hai điểm cùng nằm bên phải trục tung.

Từ điểm A ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến AB, AC đến (O) (B, C là các tiếp điểm).

a) Chứng minh: OA vuông góc với BC tại H.

b) Vẽ đường thẳng vuông góc với OB tại O cắt cạnh AC tại E. Chứng minh: ∆OAE là tam giác cân.

c) Trên tia đối của tia BC lấy điểm Q. Vẽ hai tiếp tuyến QM, QN đến (O) (M, N là tiếp tuyến). Chứng minh: 3 điểm A, M, N thẳng hàng.

Gọi M là trung điểm của đoạn thẳng AB. Trên 2 nửa phẳng đối nhau bờ AB lần lượt vẽ 2 tia Ax, By vuông góc AB. Trên Ax lấy điểm P, Trên Ay lấy Q sao cho AP = BQ. Chứng minh P, Q, M thẳng hàng.

Cho M = 2 + 2² + 2³ + … + 2²⁰. Chứng minh M chia hết cho 10.

Cho tam giác ABC vuông tại A có AH là đường cao chia cạnh huyền BC thành hai đoạn BH = 4cm; HC = 6cm.

a) Gọi M là trung điểm của AC. Tính số đo góc $\widehat{AMB}$ (làm tròn đến độ).

b) Kẻ AK vuông góc với BM (K thuộc BM). Chứng minh BK.BM = BH.BC.

Cho a, b, c thuộc ℕ^*: a² + b² = c². Chứng minh abc chia hết cho 60.

Tam giác ABC có a = 7, b = 5, góc $\widehat{C}$ = 60°. Độ dài cạnh c bằng bao nhiêu?

Cho tam giác ABC vuông tại A, đường cao AH.

a)   Biết 3AB = 2AC. Tính $sin\widehat{ACB} ,tan\widehat{ACB}$.

b) Vẽ đường phân giác CK của tam giác AHC. Biết AH = 2,4 cm; BH = 1,8 cm. Tính CH, AC, CK, $cos\widehat{HCK}$.

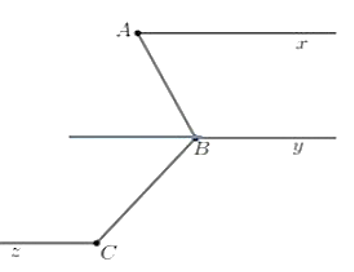
Cho hình vẽ sau biết $\widehat{xAB}=60°;\widehat{ABy}=120°;\widehat{BCz}=150°$. Chứng minh

a) Ax // By.

b) Biết $\widehat{ABC}=90°$, chứng minh Cz // By.