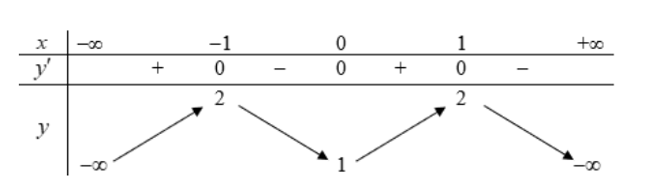
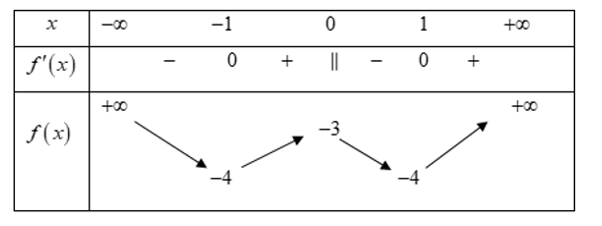
Cho hàm số có đồ thị (C). Gọi d là đường thẳng đi qua A(3; 20) và có hệ số góc m. Tìm m sao cho dường thẳng d cắt (C) tại 3 điểm phân biệt.
Câu hỏi:
Cho hàm số có đồ thị (C). Gọi d là đường thẳng đi qua A(3; 20) và có hệ số góc m. Tìm m sao cho dường thẳng d cắt (C) tại 3 điểm phân biệt.
Trả lời:
Gọi d: y = mx + n.
d đi qua A(3; 20) nên 20 = 3m + n ⇔ n = 20 – 3m hay d: y = mx + 20 – 3m
Xét phương trình hoành độ giao điểm của d và (C):
⇔
⇔
⇔
Để d cắt đồ thị tại 3 điểm phân biệt thì phương trình có 3 nghiệm phân biệt.
Suy ra phương trình có hai nghiệm phân biệt khác 3.
Điều kiện:
⇔ ⇔
Vậy để đường thẳng d cắt (C) tại 3 điểm phân biệt thì và m ≠ 24.