Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = –x + 3 có đồ thị là (d’) a) Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ. b) Hai đường thẳng (d) và (d’) cắt nhau tại C và cắt trục Ox t
Câu hỏi:
Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = –x + 3 có đồ thị là (d’)
a) Vẽ (d) và (d’) trên cùng một mặt phẳng tọa độ.
b) Hai đường thẳng (d) và (d’) cắt nhau tại C và cắt trục Ox theo thứ tự tại A và B. Tìm tọa độ các điểm A, B, C.
c) Tính chu vi và diện tích của tam giác ABC.
d) Tính góc tạo bởi đường thẳng y = x + 1 với trục Ox.
Trả lời:
Lời giải
a) Hàm số: y = x + 1
Cho x = 0 thì y = 0 + 1 = 1, ta có điểm M(0; 1)
Cho y = 0 thì 0 = x + 1 nên x = –1, ta có điểm P(–1; 0)
Đồ thị hàm số y = x + 1 là đường thẳng đi qua hai điểm M(0; 1) và P(–1; 0)
+) Hàm số: y = –x + 3
Cho x = 0 thì y = 0 + 3 = 3, ta có điểm N(0; 3)
Cho y = 0 thì 0 = –x + 3 nên x = 3, ta có điểm Q(3; 0)
Đồ thị hàm số y = –x + 3 là đường thẳng đi qua hai điểm N(0; 3) và Q(3; 0)
Ta có hình vẽ sau:
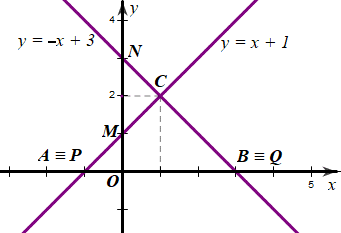
b) Hoành độ của điểm C là nghiệm của phương trình
x + 1 = –x + 3
⇔ 2x = 2
⇔ x = 1
Suy ra y = 1 + 1 = 2
Vậy C(1; 2)
Hoành độ của điểm A là nghiệm của phương trình
x + 1 = 0 ⇔ x = –1
Suy ra A(–1; 0) ≡ P
Hoành độ của điểm B là nghiệm của phương trình
–x + 3 = 0 ⇔ x = 3
Suy ra B(3; 0) ≡ Q
c) Ta có AB = OA + OB = 1 + 3 = 4
Áp dụng định lý Pytago ta có
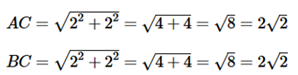
Chu vi tam giác ABC là:
![]()
Ta có:
![]()
Suy ra tam giác ABC vuông tại C
Diện tích tam giác ABC là
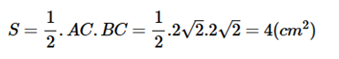
d) Xét tam giác ABC có
\(\sin {\rm{A}} = \frac{{BC}}{{AB}} = \frac{{2\sqrt 2 }}{4} = \frac{{\sqrt 2 }}{2}\)
Suy ra \(\widehat A = 45^\circ \)
Vậy góc tạo bởi đường thẳng y = x + 1 với trục Ox bằng 45°.

