Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên
Câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD // BC và AD = 2BC. Lấy M trên cạnh SA sao cho MA = 2MS.
a) Chứng minh OM // (SCD).
b) Xác định giao điểm N của MD và mặt phẳng (SBC).
Trả lời:
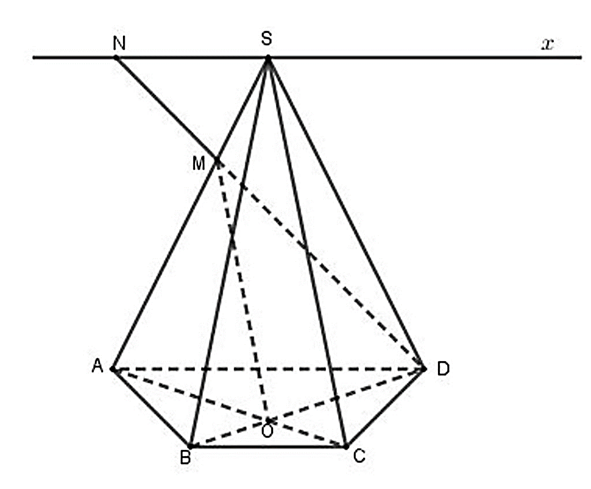
a) Do AD // BC nên \(\frac{{AO}}{{OC}} = \frac{{AD}}{{BC}} = 2\)
Mà \(\frac{{AM}}{{MS}} = 2\) nên \(\frac{{AM}}{{MS}} = \frac{{AO}}{{OC}} = 2\)
⇒ OM // SC (định lí Ta–let)
Lại có SC ⊂ (SCD) nên OM // (SCD)
b) Ta có: MD ⊂ (SAD)
* Tìm giao tuyến của (SBC) với (SAD)
Ta có: S ∈ (SAD) ∩ (SBC)
Lại có: \(\left\{ \begin{array}{l}AD \subset \left( {SAD} \right)\\BC \subset \left( {SBC} \right)\\AD\parallel BC\end{array} \right.\) ⇒ (SAD) ∩ (SBC) = Sx // AD // BC.
Do đó giao tuyến của (SBC) với (SAD) là đường thẳng đi qua S và song song với AD, BC.
Trong mặt phẳng (SAD), gọi N là giao điểm của MD với Sx.
Khi đó \(\left\{ \begin{array}{l}N \in MD\\N \in Sx \subset \left( {SBC} \right)\end{array} \right.\) ⇒ N = MD ∩ (SBC).

