Cho tam giác ABC cân tại B. Trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = CN. Kẻ BH ⊥ AC tại H. a) Chứng minh AH = HC. b) Chứng minh ∆BAN = ∆BCM. c) Gọi O là giao điểm của
Câu hỏi:
Cho tam giác ABC cân tại B. Trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N sao cho AM = CN. Kẻ BH ⊥ AC tại H.
a) Chứng minh AH = HC.
b) Chứng minh ∆BAN = ∆BCM.
c) Gọi O là giao điểm của AN và CM. Chứng minh 3 điểm B, O, H thẳng hàng.
Trả lời:
Lời giải
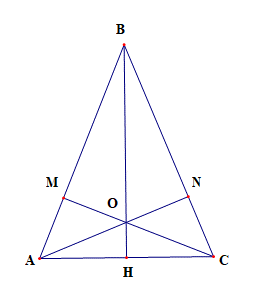
a) Xét tam giác ABC cân tại B có BH là đường cao nên đồng thời là đường trung tuyến
Do đó AH = CH.
b) Vì tam giác ABC cân tại B nên AB = BC
Ta có: AB = AM + MB; BC = BN + NC
Mà AM = CN (giả thiết) nên BM = BN
Xét ∆BAN và ∆BCM có
BM = BN (chứng minh trên);
Chung góc \(\widehat {ABC}\);
AB = BC (chứng minh trên)
Suy ra ∆BAN = ∆BCM (c.g.c)
c) Vì ∆BAN = ∆BCM (chứng minh câu b)
Nên \(\widehat {BAN} = \widehat {BCM}\) (hai góc tương ứng)
Xét tam giác AMO có
\(\widehat {AM{\rm{O}}} + \widehat {AOM} + \widehat {MAO} = 180^\circ \) (tổng ba góc trong một tam giác)
Xét tam giác CNO có
\(\widehat {{\rm{CNO}}} + \widehat {CON} + \widehat {NCO} = 180^\circ \) (tổng ba góc trong một tam giác)
Mà \(\widehat {MAO} = \widehat {NCO},\widehat {MOA} = \widehat {NOC}\)
Suy ra \(\widehat {AM{\rm{O}}} = \widehat {CNO}\)
Xét ∆MOA và ∆NOC có
\(\widehat {AM{\rm{O}}} = \widehat {CNO}\) (chứng minh trên);
AM = CN (giả thiết);
\(\widehat {MAO} = \widehat {NCO}\) (chứng minh trên)
Suy ra ∆MOA = ∆NOC (g.c.g)
Do đó OA = OC (hai cạnh tương ứng)
Xét ∆BOA và ∆BOC có
OA = OC (chứng minh trên);
\(\widehat {BAO} = \widehat {BCO}\) (chứng minh trên);
BA = BC (chứng minh câu b)
Suy ra ∆BOA = ∆BOC (c.g.c)
Do đó \(\widehat {ABO} = \widehat {CBO}\) (hai góc tương ứng)
Suy ra BO là tia phân giác của \(\widehat {ABC}\) (1)
Xét tam giác ABC cân tại B có
BH là đường cao
Suy ra BH là tia phân giác của \(\widehat {ABC}\) (2)
Từ (1) và (2) suy ra ba điểm 3 điểm B, O, H thẳng hàng.

