Câu hỏi:
Biết hàm số f(x) xác định trên R và có đạo hàm f’(x) = (x – 1)x2(x + 1)3(x + 2)4. Hỏi hàm số có bao nhiêu điểm cực trị?
A. 4.
B. 1
C. 2
D. 3
Trả lời:
Đáp án C.
f’(x) = (x – 1)x2(x + 1)3(x + 2)4
Ta thấy phương trình f’(x) = 0 có 2 nghiệm đơn là 1; -1 và có hai nghiệm kép là 0; -2
Từ đó số điểm cực trị là 2.
Câu 1:
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
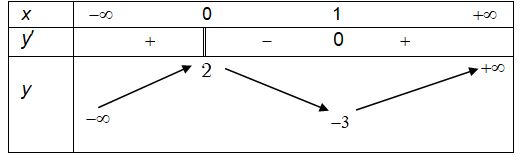
Khẳng định nào sau đây là khẳng định đúng?
Câu 3:
Cho các phát biểu sau:
I. Đồ thị hàm số có y = x4 – x + 2 có trục đối xứng là Oy.
II. Hàm số f(x) liên tục và có đạo hàm trên khoảng (a;b) đạt cực trị tại điểm x0 thuộc khoảng (a;b) thì tiếp tuyến tại điểm M(x0,f(x0)) song song với trục hoành.
III. Nếu f(x) nghịch biến trên khoảng (a;b) thì hàm số không có cực trị trên khoảng (a;b).
IV. Hàm số f(x) xác định và liên tục trên khoảng (a;b) và đạt cực tiểu tại điểm x0 thuộc khoảng (a;b) thì f(x) nghịch biến trên khoảng (a;x0) và đồng biến trên khoảng (x0;b).
Các phát biểu đúng là:
