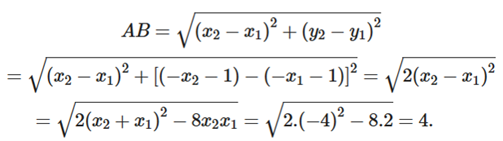Cho A, B là giao điểm của đồ thị hàm số y = 2x + 1/x + 1 và đường thẳng y = – x – 1. A. AB = 4; B. AB = căn bậc hai của 2; C. AB = 2 căn bậc hai của 2; D. AB = 4 căn bậc hai của 2

❮ Bài trước Bài sau ❯

Câu hỏi:

Cho A, B là giao điểm của đồ thị hàm số \(y = \frac{{2{\rm{x}} + 1}}{{x + 1}}\) và đường thẳng y = – x – 1.

A. AB = 4;

B. \[{\rm{A}}B = \sqrt 2 \];

C. \[{\rm{A}}B = 2\sqrt 2 \];

D. \[{\rm{A}}B = 4\sqrt 2 \].

Trả lời:

Lời giải

Đáp án đúng là: A

Phương trình hoành giao điểm là

\(\frac{{2{\rm{x}} + 1}}{{x + 1}} = - x - 1\) (x≠ – 1)

⇔ 2x + 1 = (x + 1)( – x – 1)

⇔ 2x + 1 = – x² – 2x – 1

⇔ x² + 4x + 2 = 0

Gọi x₁, x₂ là hai nghiệm của phương trình trên

Theo Vi – ét ta có:

x₁ + x₂ = –4 và x₁ . x₂ = 2

Tọa độ các điểm A(x₁; y₁) và B(x₂; y₂)

Độ dài đoạn thẳng AB là

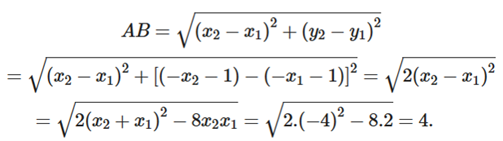
Media VietJack

Vậy ta chọn đáp án A.

Xem thêm bài tập Toán có lời giải hay khác:

Câu 1:

Nhân ngày 20 tháng 10 một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiện của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy Thu Ngân:

a) Chị Hoa không có thẻ khách hàng thân thiện của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1 050 000 đồng. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?

b) Cô Hà có thẻ khách hàng thân thiện, cô mua 1 chiếc túi xách và nhận được một voucher trị giá 91 000 đồng. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?

Xem lời giải »

Câu 2:

Tam giác ABC có BC = 21 cm, CA = 17 cm, AB = 10 cm. Tính bán kính R của đường tròn ngoại tiếp tam giác ABC

Xem lời giải »

Câu 3:

Tìm tất cả các số nguyên x, y, z thỏa mãn 3x² + 6y² + 2z² + 3y²z² – 18x = 6.

Xem lời giải »

Câu 4:

Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu H trên AB, AC. Chứng minh:

a) \(\frac{{FB}}{{FC}} = \frac{{A{B^3}}}{{A{C^3}}}\);

b) BC² = 3AH² + BE² + CF²;

c) \(BE\sqrt {CH} + CF\sqrt {BH} = AH\sqrt {BC} \).