Cho đoạn thẳng AB có độ dài 2a .Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua trung điểm của M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ
Câu hỏi:
Cho đoạn thẳng AB có độ dài 2a .Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua trung điểm của M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí của các điểm C, D sao cho tam giác MCD có diện tích nhỏ nhất . Tính diện tích tam giác đó.
Trả lời:
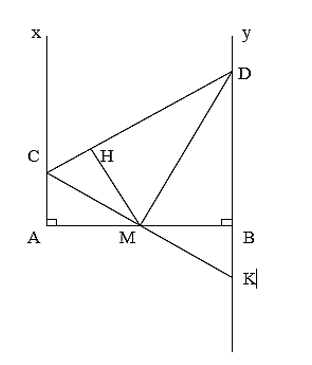
Gọi K là giao điểm của CM và DB
MA = MB; ;
Mặt khác
cân tại tại D
Kẻ
khi đó
Vậy min . Các điểm C, D được xác định trên Ax; By sao cho AC = BD = a .

