Cho đường tròn đường kính AB vẽ tiếp tuyến Ax , By từ M trên đường tròn M khác A
Câu hỏi:
Cho đường tròn đường kính AB vẽ tiếp tuyến Ax , By từ M trên đường tròn M khác A, B vẽ tiếp tuyến thứ 3 nó cắt Ax tại C cắt By tại D gọi N là giao điểm của BC và AO.
a) Chứng minh: \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\).
b) Chứng minh: MN vuông góc AB.
c) Chứng minh: \(\widehat {COD} = 90^\circ \).
Trả lời:
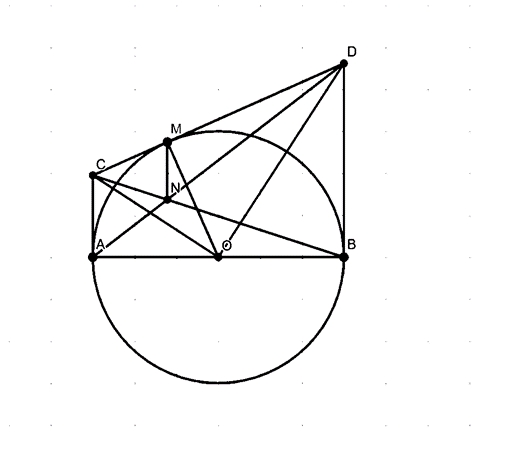
a) Vì CA,CM là tiếp tuyến của (O).
Suy ra: CA = CM
Tương tự DB = DM
Vì AC,DB là tiếp tuyến của (O)
Suy ra: AC ⊥ AB, BD ⊥ AB
⇒ AC // BD
⇒ \(\frac{{CN}}{{NB}} = \frac{{AC}}{{BD}} = \frac{{CM}}{{MD}}\)
⇒ \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\)
b) Từ câu a có: \(\frac{{CN}}{{NB}} = \frac{{AC}}{{BD}} = \frac{{CM}}{{MD}}\) nên MN // BD
Vì BD vuông góc AB nên MN ⊥ AB
c) Ta có: CM, CA là tiếp tuyến của (O) nên OC là tia phân giác của \(\widehat {AOM}\)
Tương tự: OD là phân giác của \(\widehat {BOM}\)
Mà: \(\widehat {AOM} + \widehat {BOM} = \widehat {AOB} = 180^\circ \)
Suy ra: \(\frac{1}{2}\left( {\widehat {AOM} + \widehat {BOM}} \right) = 90^\circ \)
Hay: \(\widehat {COM} + \widehat {DOM} = \widehat {COD} = 90^\circ \)
Vậy \(\widehat {COD} = 90^\circ \).

