Cho đường tròn (O;R). Từ điểm A ở ngoài đường tròn (giả sử OA = 2R) vẽ 2 tiếp tuyến AB, AC với (O)
Câu hỏi:
Cho đường tròn (O;R). Từ điểm A ở ngoài đường tròn (giả sử OA = 2R) vẽ 2 tiếp tuyến AB, AC với (O) (B, C là 2 tiếp điểm). Chứng minh ΔABC đều.
Trả lời:
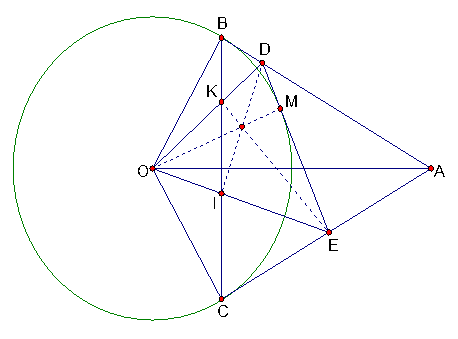
Vì AB là tiếp tuyến của (O) nên AB vuông góc với OB
Áp dụng hệ thức lượng trong tam giác vuông OBA có:
sin . Suy ra:
Xét ∆ABO và ∆ACO có:
Chung OA
OB = OC (đều là bán kính (O))
AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra: ∆ABO = ∆ACO (c.c.c)
⇒
⇒
Vì AB = AC nên tam giác ABC cân tại A
Mà
Nên ∆ABC là tam giác đều.

