Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp chung ngoài DE, D ∈ (O), E ∈ (O’). Kẻ tiếp tuyến chung trong tại A cắt DE ở I. Gọi M là giao điểm của OI và AD, N là giao điểm của O’I và AE.

a) Tứ giác AMIN là hình gì? Vì sao?

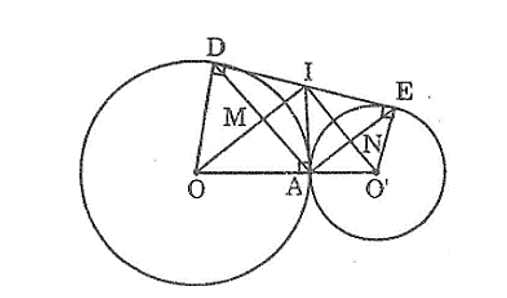
a) Trong đường tròn (O) ta có OI là tia phân giác của $\widehat{AID}$ (tính chất hai tiếp tuyến cắt nhau)

Trong đường tròn (O’) ta có O’I là tia phân giác của $\widehat{AIE}$ (tính chất hai tiếp tuyến cắt nhau)

⇒ IO ⊥ IO’ (tính chất hai góc kề bù)

Suy ra $\widehat{\text{OIO}\text{'}}=90°$hay $\widehat{\text{MIN}}=90°$

Lại có: IA = ID (tính chất hai tiếp tuyến cắt nhau)

Suy ra tam giác ADI cân tại I

Tam giác cân AID có IO là phân giác của $\widehat{AID}$nên IO cũng là đường cao của tam giác AID

Suy ra: IO ⊥ AD hay $\widehat{IMA}=90°$

Mặt khác: IA = IE (tính chất hai tiếp tuyến cắt nhau)

Suy ra tam giác AEI cân tại I

Tam giác cân AIE có IO’ là phân giác của góc AIE nên IO’ cũng là đường cao của tam giác AIE

Suy ra: IO’ ⊥ AE hay $\widehat{ANI}=90°$

Tứ giác AMIN có ba góc vuông nên nó là hình chữ nhật.