Cho hình bình hành ABCD có AB = 2BC. Gọi E và F theo thứ tự là trung điểm của AB, CD.
Câu hỏi:
Cho hình bình hành ABCD có AB = 2BC. Gọi E và F theo thứ tự là trung điểm của AB, CD.
a) Chứng minh DEBF là hình bình hành.
b) Chứng minh ADFE là hình thoi.
c) Gọi M là giao điểm của DE và AF, N là giao điểm của CE và BF. Chứng minh EMFN là hình chữ nhật.
Trả lời:
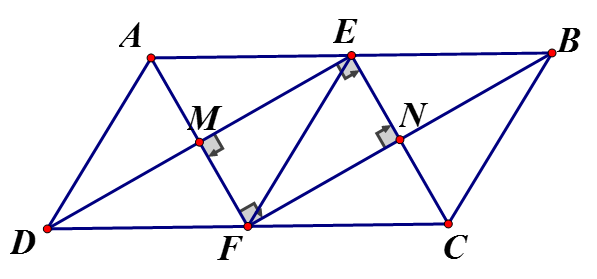
a) Ta có: AB = DC (tính chất hình bình hành) mà E, F lần lượt là trung điểm AB, CD
⇒ EB = DF và EB // DF
⇒ BEDF là hình bình hành
b) AE = DF(= AB = DC) và AE // DF
⇒ AEFD là hình bình hành
Mà AE = AD (= AB)
⇒ AEFD là hình thoi
c) EBFD là hình bình hành ⇒ ED // BF ⇒ EM // FN(1)
Chứng minh tương tự câu b ⇒ EBCF là hình thoi
Và AEFD, EBCF là hình thoi
⇒ EM = FN và FN = NB mà ED = BF ⇒ ME = FN(2)
Từ (1) và (2) suy ra EMFN là hình bình hành mà = 90°(AEFD là hình thoi)
⇒ EMFN là hình chữ nhật.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Cho hình thoi ABCD có cạnh bằng a và = 60°. Độ dài của vectơ ?
Xem lời giải »
Câu 2:
Cho tam giác ABC có AB = AC và M là trung điểm của BC. Gọi N là trung điểm của AB, trên tia đối của NC lấy điểm K sao cho NK = NC.
a) Chứng minh ∆ABM = ∆CMA.
b) Chứng minh AK = 2MC.
c) Tính .
Xem lời giải »
Câu 3:
Cho tam giác ABC có AB = c, BC = a, AC = b thỏa mãn: b2 + c2 – a2 = . Tính số đo .
Xem lời giải »
Câu 4:
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB = 3,6 cm HC = 6,4 cm.
a) Tính AB, AC, AH.
b) Kẻ HE vuông góc AB, HF vuông góc AC. Chứng minh AB.AE = AC.AF.
Xem lời giải »
Câu 5:
Có bao nhiêu số nguyên sau khi làm tròn trăm cho kết quả là 6700?
Xem lời giải »
Câu 6:
Hai đoạn ống nước có chiều dài lần lượt là 0,8 m và 1,35 m. Người ta nối hai đầu ống để tạo thành một ống nước mới. Chiều dài của phần nối chung là m. Hỏi đoạn ống nước mới dài bao nhiêu mét?
Xem lời giải »


