Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy và cạnh bên cùng bằng a. Tính thể
Câu hỏi:
Cho hình lăng trụ đều ABC.A'B'C' có cạnh đáy và cạnh bên cùng bằng a. Tính thể tích của khối lăng trụ đó.
Trả lời:
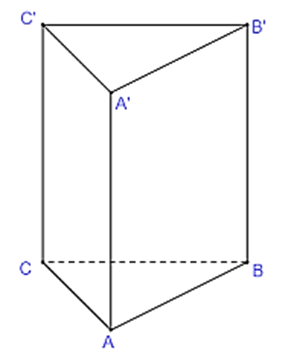
Khối lăng trụ đều là khối lăng trụ đứng có các cạnh bên và các cạnh đáy bằng nhau.
Vì ABC.A'B'C' là lăng trụ đều nên AA' ⏊ (ABC) và tam giác ABC đều.
Tam giác ABC là tam giác đều có cạnh a nên \({S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{4}\)
Cạnh bên của lăng trụ bằng a nên AA' = a
Vậy thể tích của khối lăng trụ đã cho là:
\({V_{ABC.A'B'C'}} = AA'\,.\,{S_{\Delta ABC}} = a\,.\,\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{4}\).