Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N. Chứng minh
Câu hỏi:
Cho hình thang ABCD có AB // CD (AB < CD) và M là trung điểm của AD. Qua M vẽ đường thẳng song song với hai đáy của hình thang cắt hai đường chéo BD và AC tại E và F, cắt BC tại N. Chứng minh rằng N, E, F lần lượt là trung điểm của BC, BD, AC.
Trả lời:
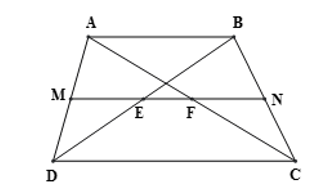
Xét hình thang ABCD có:
MA = MD
N ∈ BC
MN // AB // CD
Suy ra N là trung điểm của BC.
Xét có:
MA = MD; MF // DC
⇒ FA = FC ⇒ F là trung điểm của AC.
Xét có:
MA = MD; ME // AB
⇒ DE = BE ⇒ E là trung điểm của BD
