Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB. a) Chứng minh
Câu hỏi:
Cho tam giác ABC có A’, B’, C’ lần lượt là trung điểm của BC, CA, AB.
a) Chứng minh: \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \).
b) Tìm các vectơ bằng \(\overrightarrow {B'C'} ,\overrightarrow {C'A'} \).
Trả lời:
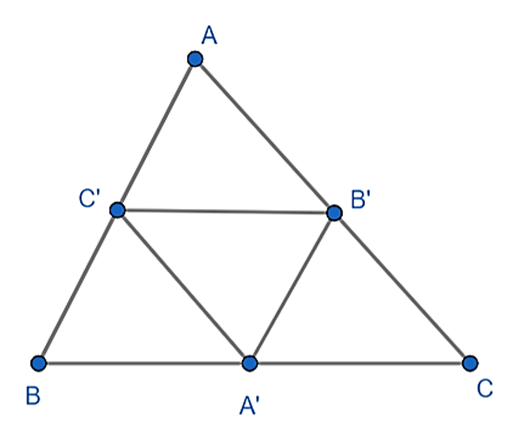
a) Vì B’, C’ lần lượt là trung điểm của CA và AB
Nên B’C’ là đường trung bình của tam giác ABC
Suy ra: B’C’ // BC và B’C’ = \(\frac{1}{2}BC = A'B = A'C\)
Suy ra: \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \)
b) \(\overrightarrow {B'C'} = \overrightarrow {CA'} = \overrightarrow {A'B} \)
\(\overrightarrow {C'A'} = \overrightarrow {AB'} = \overrightarrow {B'C} \).

