Cho tam giác ABC có AB = 2, AC = 3, góc A = 60 độ. Tính độ dài phân giác
Câu hỏi:
Cho tam giác ABC có AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính độ dài phân giác góc A?
Trả lời:
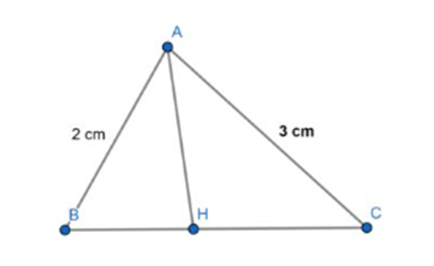
Áp dụng định lý hàm số cosin cho ΔABC ta có:
BC2 = BA2 + AC2 – 2.AB.AC.cos\(60^\circ \)= \( = 4 + 9 - 2.2.3.\cos 60^\circ = 7\)
Suy ra: BC = \(\sqrt 7 \)
Áp dụng tính chất đường phân giác cho ΔABC:
\(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)
Suy ra: \(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{5}{{\sqrt 7 }}\)
BH = \(AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)
\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2.AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)
Xét tam giác ABH có:
AH2 = AB2 + BH2 – 2.AB.BH. cos\(\widehat B\)= \(\frac{{108}}{{25}}\)
Suy ra: AH = \(\frac{{6\sqrt 3 }}{5}\).