Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh
Câu hỏi:
Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB. Phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng bao nhiêu?
A. \( - \frac{1}{2}\)
B. \(\frac{1}{2}\)
C. \(\frac{2}{3}\)
D. \( - \frac{1}{3}\).
Trả lời:
Đáp án đúng là: A
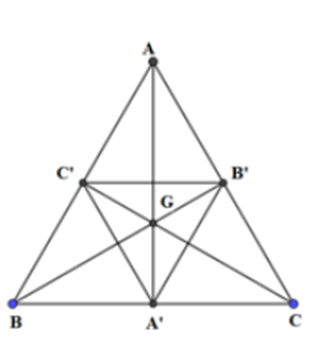
Vì G là trọng tâm tam giác ABC
Nên \(\overrightarrow {GA'} = \frac{{ - 1}}{2}\overrightarrow {GA} ;\overrightarrow {GB'} = \frac{{ - 1}}{2}\overrightarrow {GB} ;\overrightarrow {GC'} = \frac{{ - 1}}{2}\overrightarrow {GC} \)
Suy ra phép vị tự tâm G biến tam giác ABC thành tam giác A’B’C’ có tỉ số vị tự bằng \( - \frac{1}{2}\)
Vậy ta chọn đáp án A.

