Cho tam giác ABC, gọi D là trung điểm của AB, trên tia BC lấy điểm E và F sao cho BE = EF = FC. Trên tia đối của tia BA lấy điểm G sao cho BG = BD. Chứng minh: AF, CD, GE đồng quy.
Câu hỏi:
Cho tam giác ABC, gọi D là trung điểm của AB, trên tia BC lấy điểm E và F sao cho BE = EF = FC. Trên tia đối của tia BA lấy điểm G sao cho BG = BD. Chứng minh: AF, CD, GE đồng quy.
Trả lời:
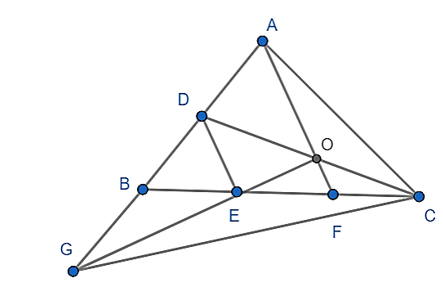
Gọi giao điểm của AF và CD là O.
∆ABF có D, E là trung điểm AB, BF nên DE là đường trung bình của tam giác ABF
⇒ DE // AF hay DE // OF
∆CDE có OF // DE, F là trung điểm CE nên O là trung điểm của CD.
Xét ∆CDG có: CE = CB, CB là đường trung tuyến
Nên E là trọng tâm của ∆CDG
Hay GE đi qua trung điểm CD tức GE đi qua O.
Vậy AF, CD, GE đồng quy tại O.

