Cho tam giác ABC nội tiếp đường tròn (O;R). Các đường cao AD, BE, CF cắt nhau tại H. Chứng minh: Tứ giác BFCE nội tiếp.
Câu hỏi:
Cho tam giác ABC nội tiếp đường tròn (O;R). Các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh: Tứ giác BFCE nội tiếp.
Trả lời:
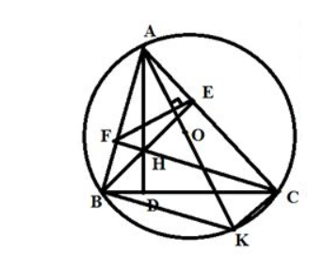
Ta có: = = 90° (Vì BE và CF là đường cao)
Mà 2 góc này cùng thuộc 1 nửa mặt phẳng bờ BC nên tứ giác BFCE nội tiếp.

