Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt
Câu hỏi:
Cho tam giác ABC nội tiếp đường tròn tâm O. Các tia phân giác của các góc A và B cắt nhau ở I và cắt đường tròn theo thứ tự ở D và E. Chứng minh:
a, Tam giác BDI là tam giác cân.
b, DE là đường trung trực của IC.
c, IF và BC song song, trong đó F là giao điểm của DE và AC.
Trả lời:
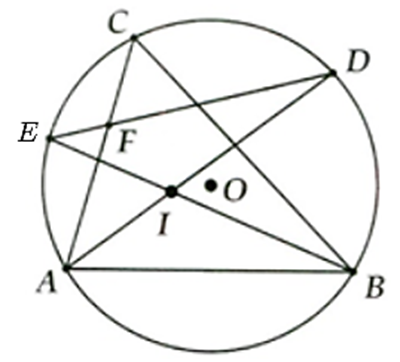
a, \(\widehat {BID} = \frac{1}{2}\)sđ
⇒ ∆BID cân ở D
b, Chứng minh tương tự: ∆IEC cân tại E, ∆DIC cân tại D
⇒ EI = EC và DI = DC
⇒ DE là trung trực của CI
c, F ∈ DE nên FI = FC
⇒ IF // BC.
Xem thêm bài tập Toán có lời giải hay khác:
Câu 1:
Tìm tất cả giá trị của tham số m để hàm số y = mx2 – (m + 6)x nghịch biến trên khoảng (–1; +∞).
Xem lời giải »
Câu 2:
Tính bằng cách thuận tiện: \(\frac{1}{4}:0,25 - \frac{1}{8}:0,125 + \frac{1}{2}:0,5 - \frac{1}{{10}}\).
Xem lời giải »
Câu 3:
Xe thứ nhất chở được 25 tấn hàng, xe thứ hai chở 35 tấn hàng, xe thứ ba chở bằng trung bình cộng 3 xe. Hỏi xe thứ 3 chở bao nhiêu tấn hàng?
Xem lời giải »
Câu 4:
A = {1; 2; 3; …; 16}. Bốc ngẫu nhiên 3 phần tử trong A. Tính xác suất để để tổng 3 số bốc ra chia hết cho 3.
Xem lời giải »
Câu 5:
Tính bán kính đường tròn ngoại tiếp tam giác đều cạnh a.
Xem lời giải »
Câu 6:
Hình thang có đáy lớn hơn đáy bé 20,4 dm và bằng \(\frac{5}{3}\) đáy bé, chiều cao hơn đáy bé 2,1 dm. Tính diện tích hình thang.
Xem lời giải »
Câu 7:
Tìm nghiệm nguyên dương của phương trình x + y + z = 2xyz.
Xem lời giải »
Câu 8:
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC có A(–1;1), B(1;3) và trọng tân là G\(\left( { - 2;\frac{2}{3}} \right)\). Tìm tọa độ điểm M trên tia Oy sao cho tam giác MBC vuông tại M.
Xem lời giải »


