Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác ANEM là hình chữ nhật.

Cho tam giác ABC vuông tại A (AB < AC). Gọi M, N, E lần lượt là trung điểm của AB, AC, BC. Chứng minh rằng tứ giác ANEM là hình chữ nhật.

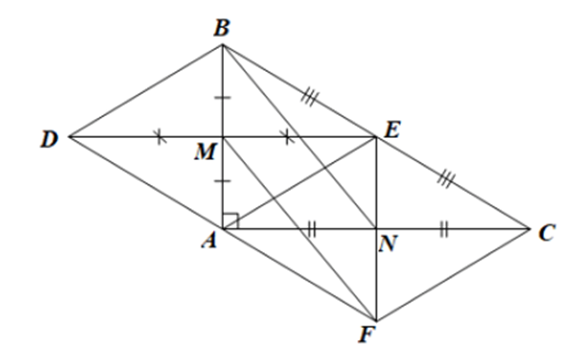
Xét ΔABC vuông tại A có:

AE là đường trung tuyến ứng với cạnh huyền BC

Suy ra

Ta có: EA = EC nên E nằm trên đường trung trực của AC.

N là trung điểm của AC nên N nằm trên đường trung trực của AC.

Þ EN là đường trung trực của đoạn thẳng AC nên EN ⊥ AC

Lại có: EA = EB nên E nằm trên đường trung trực của AB.

M là trung điểm của AB nên M nằm trên đường trung trực của AB.

Þ EM là đường trung trực của AB nên EM ⊥ AB hay 0$\widehat{AME}=90°$

Tứ giác AMEN có: $\widehat{ANE}=\widehat{AME}=\widehat{MAN}=90°$

Þ ANEM là hình chữ nhật

Vậy ANEM là hình chữ nhật.