Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của góc ACH cắt AH tại M, kẻ phân giác của góc BaH cắt BH tại N. Chứng minh rằng MN // AB.

Cho tam giác ABC vuông tại A. Đường cao AH. Kẻ phân giác của $\widehat{ACH}$ cắt AH tại M, kẻ phân giác của $\widehat{BAH}$ cắt BH tại N. Chứng minh rằng MN // AB.

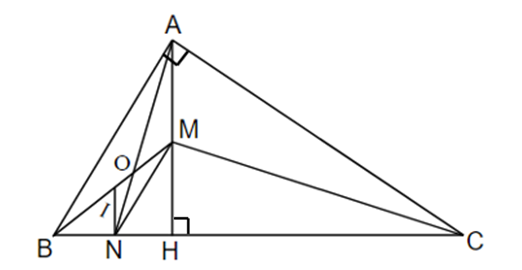
Áp dụng định lý đường phân giác trong tam giác ta có:

$\frac{AM}{HM}=\frac{AC}{HC};\frac{BN}{HN}=\frac{AB}{AH}$

Xét ΔAHB và ΔCHA có:

$\widehat{AHB}=\widehat{CHA}=90°$

AH chung

$\widehat{BAH}=\widehat{ACH}$ (cùng phụ với $\widehat{CAH}$)

Do đó ΔAHB ᔕ ΔCHA (g.g)

Suy ra $\frac{AB}{AH}=\frac{AC}{HC}$

Do đó, $\frac{AM}{HM}=\frac{BN}{HN}$

Suy ra MN // AB (định lý Ta-let đảo)

Vậy MN // AB.